statsmodels 主成分分析¶
关键思想:主成分分析、世界银行数据、生育率
在本笔记本中,我们使用主成分分析 (PCA) 来分析 192 个国家生育率的时间序列,使用从世界银行获得的数据。主要目标是了解生育率随时间的趋势在不同国家之间的差异。这是一个略微不典型的 PCA 说明,因为数据是时间序列。此类设置已开发出诸如功能 PCA 之类的方法,但由于生育率数据非常平滑,因此在这种情况下使用标准 PCA 并无真正的不利之处。
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.multivariate.pca import PCA
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
数据可以从 世界银行网站 获取,但在这里我们使用经过稍微清理的数据版本
[2]:
data = sm.datasets.fertility.load_pandas().data
data.head()
[2]:
| 国家名称 | 国家代码 | 指标名称 | 指标代码 | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | ... | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 阿鲁巴 | ABW | 总生育率(每个妇女的出生数) | SP.DYN.TFRT.IN | 4.820 | 4.655 | 4.471 | 4.271 | 4.059 | 3.842 | ... | 1.786 | 1.769 | 1.754 | 1.739 | 1.726 | 1.713 | 1.701 | 1.690 | NaN | NaN |
| 1 | 安道尔 | AND | 总生育率(每个妇女的出生数) | SP.DYN.TFRT.IN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | 1.240 | 1.180 | 1.250 | 1.190 | 1.220 | NaN | NaN | NaN |
| 2 | 阿富汗 | AFG | 总生育率(每个妇女的出生数) | SP.DYN.TFRT.IN | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | ... | 7.136 | 6.930 | 6.702 | 6.456 | 6.196 | 5.928 | 5.659 | 5.395 | NaN | NaN |
| 3 | 安哥拉 | AGO | 总生育率(每个妇女的出生数) | SP.DYN.TFRT.IN | 7.316 | 7.354 | 7.385 | 7.410 | 7.425 | 7.430 | ... | 6.704 | 6.657 | 6.598 | 6.523 | 6.434 | 6.331 | 6.218 | 6.099 | NaN | NaN |
| 4 | 阿尔巴尼亚 | ALB | 总生育率(每个妇女的出生数) | SP.DYN.TFRT.IN | 6.186 | 6.076 | 5.956 | 5.833 | 5.711 | 5.594 | ... | 2.004 | 1.919 | 1.849 | 1.796 | 1.761 | 1.744 | 1.741 | 1.748 | NaN | NaN |
5 行 × 58 列
在这里,我们构建一个仅包含数值生育率数据的 DataFrame,并将索引设置为国家名称。我们还删除了所有包含任何缺失数据的国家。
[3]:
columns = list(map(str, range(1960, 2012)))
data.set_index("Country Name", inplace=True)
dta = data[columns]
dta = dta.dropna()
dta.head()
[3]:
| 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | ... | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 国家名称 | |||||||||||||||||||||
| 阿鲁巴 | 4.820 | 4.655 | 4.471 | 4.271 | 4.059 | 3.842 | 3.625 | 3.417 | 3.226 | 3.054 | ... | 1.825 | 1.805 | 1.786 | 1.769 | 1.754 | 1.739 | 1.726 | 1.713 | 1.701 | 1.690 |
| 阿富汗 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | ... | 7.484 | 7.321 | 7.136 | 6.930 | 6.702 | 6.456 | 6.196 | 5.928 | 5.659 | 5.395 |
| 安哥拉 | 7.316 | 7.354 | 7.385 | 7.410 | 7.425 | 7.430 | 7.422 | 7.403 | 7.375 | 7.339 | ... | 6.778 | 6.743 | 6.704 | 6.657 | 6.598 | 6.523 | 6.434 | 6.331 | 6.218 | 6.099 |
| 阿尔巴尼亚 | 6.186 | 6.076 | 5.956 | 5.833 | 5.711 | 5.594 | 5.483 | 5.376 | 5.268 | 5.160 | ... | 2.195 | 2.097 | 2.004 | 1.919 | 1.849 | 1.796 | 1.761 | 1.744 | 1.741 | 1.748 |
| 阿拉伯联合酋长国 | 6.928 | 6.910 | 6.893 | 6.877 | 6.861 | 6.841 | 6.816 | 6.783 | 6.738 | 6.679 | ... | 2.428 | 2.329 | 2.236 | 2.149 | 2.071 | 2.004 | 1.948 | 1.903 | 1.868 | 1.841 |
5 行 × 52 列
有两种方法可以使用 PCA 来分析矩形矩阵:我们可以将行视为“对象”,将列视为“变量”,反之亦然。在这里,我们将生育率指标视为“变量”,用于衡量国家作为“对象”。因此,目标将是将每年的生育率值减少到少量生育率“概况”或“基函数”,这些函数捕获不同国家随着时间的推移的大部分变化。
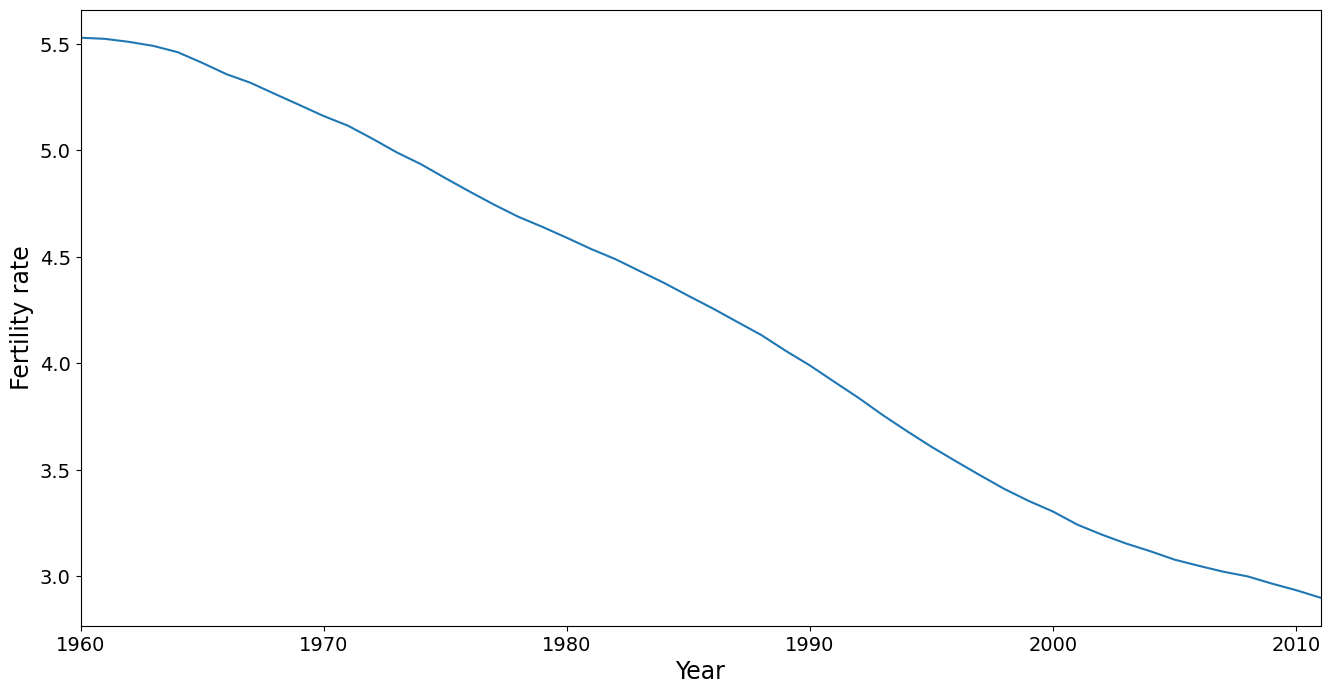
在 PCA 中会去除平均趋势,但仔细查看它还是很有价值的。它表明生育率在该数据集中涵盖的时间段内稳步下降。请注意,平均值是使用国家作为分析单位计算的,忽略了人口规模。这对于下面进行的 PC 分析也是如此。更复杂的分析可能会对国家进行加权,例如 1980 年的人口。
[4]:
ax = dta.mean().plot(grid=False)
ax.set_xlabel("Year", size=17)
ax.set_ylabel("Fertility rate", size=17)
ax.set_xlim(0, 51)
[4]:
(0.0, 51.0)
接下来,我们执行 PCA
[5]:
pca_model = PCA(dta.T, standardize=False, demean=True)
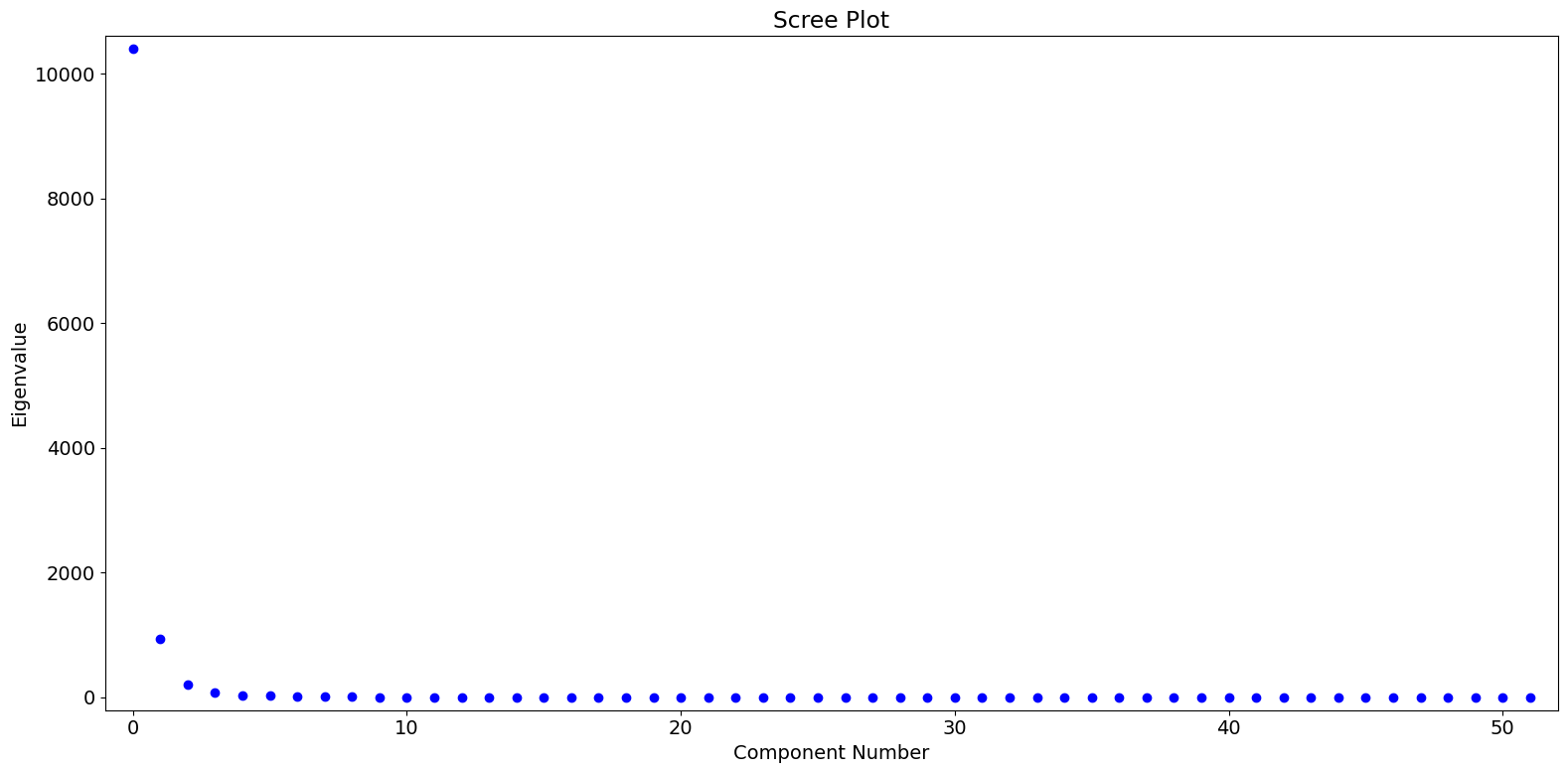
根据特征值,我们看到第一个 PC 占主导地位,第二个和第三个 PC 可能捕捉到一小部分有意义的变化。
[6]:
fig = pca_model.plot_scree(log_scale=False)
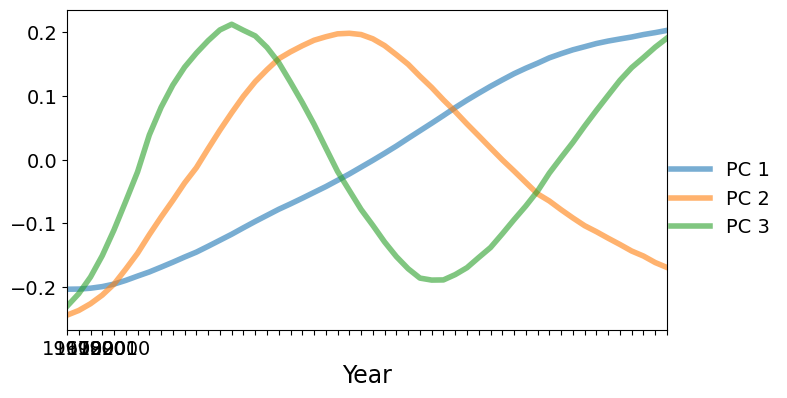
接下来,我们将绘制 PC 因子。主导因子单调递增。在第一个因子上得分较高的国家将比上面显示的平均水平增长更快(或下降更慢)。在第一个因子上得分较低的国家将比平均水平下降更快。第二个因子呈 U 形,在 1985 年左右有一个正峰值。在第二个因子上有很大正得分的国家,在数据范围的开始和结束时生育率将低于平均水平,但在数据范围的中间生育率高于平均水平。
[7]:
fig, ax = plt.subplots(figsize=(8, 4))
lines = ax.plot(pca_model.factors.iloc[:, :3], lw=4, alpha=0.6)
ax.set_xticklabels(dta.columns.values[::10])
ax.set_xlim(0, 51)
ax.set_xlabel("Year", size=17)
fig.subplots_adjust(0.1, 0.1, 0.85, 0.9)
legend = fig.legend(lines, ["PC 1", "PC 2", "PC 3"], loc="center right")
legend.draw_frame(False)
/tmp/ipykernel_3281/427128218.py:3: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
ax.set_xticklabels(dta.columns.values[::10])
为了更好地理解正在发生的事情,我们将绘制具有相似 PC 得分的一组国家的生育率轨迹。以下便利函数会生成这样的图。
[8]:
idx = pca_model.loadings.iloc[:, 0].argsort()
首先,我们绘制了在 PC 1 上得分最高的五个国家。这些国家的生育率增长率高于全球平均水平(全球平均水平呈下降趋势)。
[9]:
def make_plot(labels):
fig, ax = plt.subplots(figsize=(9, 5))
ax = dta.loc[labels].T.plot(legend=False, grid=False, ax=ax)
dta.mean().plot(ax=ax, grid=False, label="Mean")
ax.set_xlim(0, 51)
fig.subplots_adjust(0.1, 0.1, 0.75, 0.9)
ax.set_xlabel("Year", size=17)
ax.set_ylabel("Fertility", size=17)
legend = ax.legend(
*ax.get_legend_handles_labels(), loc="center left", bbox_to_anchor=(1, 0.5)
)
legend.draw_frame(False)
[10]:
labels = dta.index[idx[-5:]]
make_plot(labels)
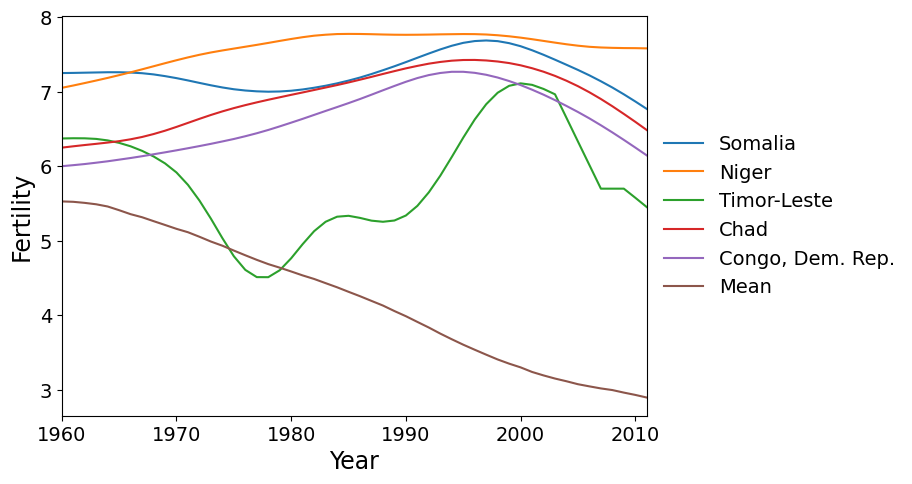
以下是因子 2 得分最高的五个国家。这些国家在 1980 年左右达到生育率峰值,比世界其他大多数国家晚,随后生育率迅速下降。
[11]:
idx = pca_model.loadings.iloc[:, 1].argsort()
make_plot(dta.index[idx[-5:]])
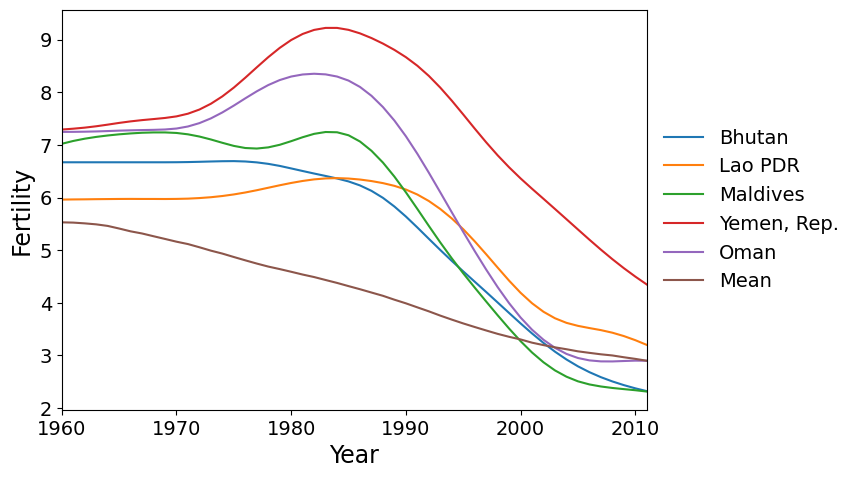
最后,我们有在 PC 2 上得分最低的国家。这些国家的生育率在 1960 年代和 1970 年代下降的速度远快于全球平均水平,然后趋于平缓。
[12]:
make_plot(dta.index[idx[:5]])
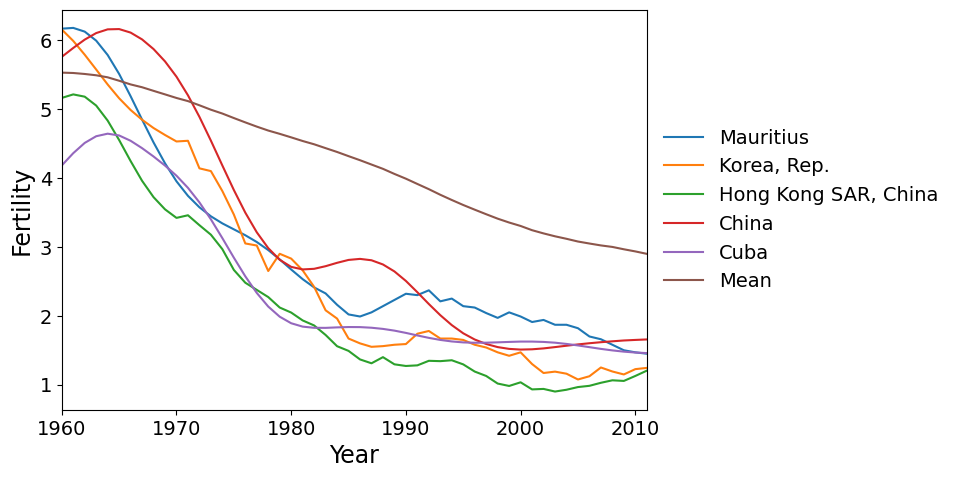
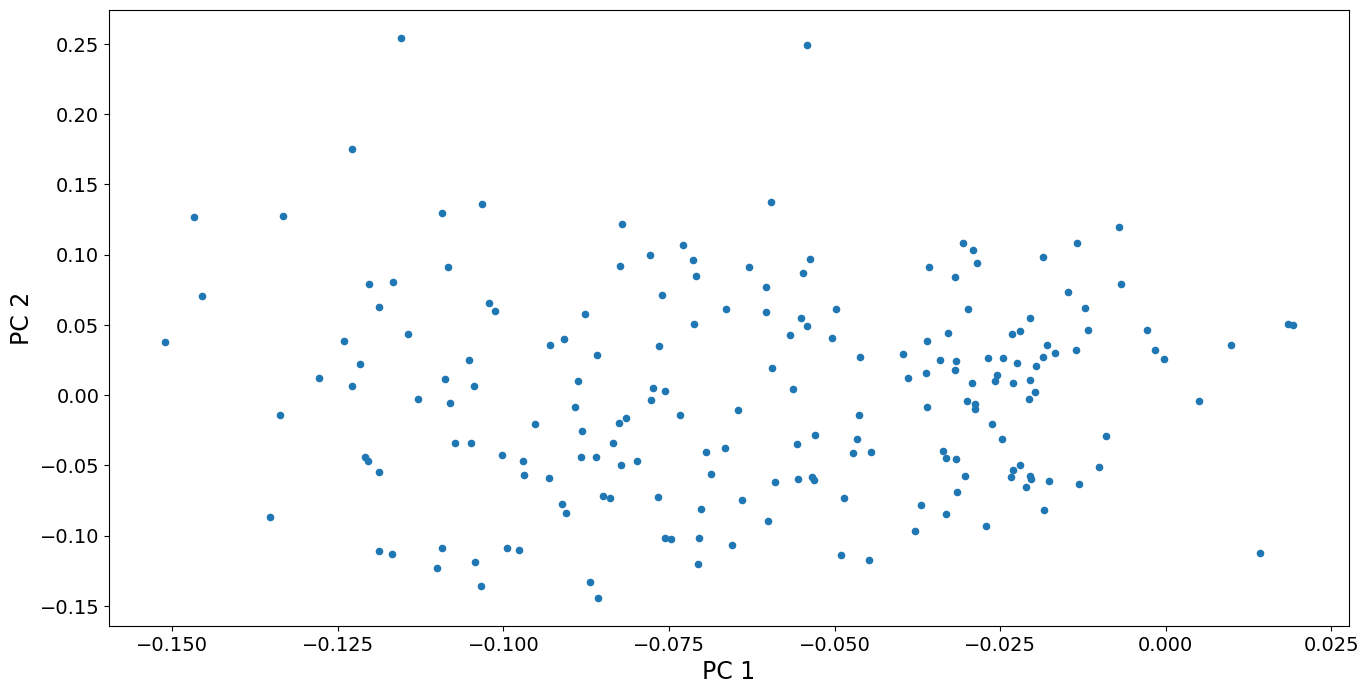
我们还可以查看前两个主成分得分的散点图。我们看到,国家之间的差异相当连续,除了也许得分最高的两个国家在 PC 2 上有些偏离其他点。这些国家,阿曼和也门,在 1980 年左右的生育率出现了急剧的激增,这是独一无二的。没有其他国家出现过这样的激增。相反,在 PC 1 上得分高的国家(生育率持续上升)是差异连续体的一部分。
[13]:
fig, ax = plt.subplots()
pca_model.loadings.plot.scatter(x="comp_00", y="comp_01", ax=ax)
ax.set_xlabel("PC 1", size=17)
ax.set_ylabel("PC 2", size=17)
dta.index[pca_model.loadings.iloc[:, 1] > 0.2].values
[13]:
array(['Oman', 'Yemen, Rep.'], dtype=object)