拟二项式回归¶
此笔记本演示了如何使用自定义方差函数和非二进制数据与拟二项式 GLM 族一起执行回归分析,使用作为比例的因变量。
此笔记本使用大麦叶斑病数据,该数据已在多本教科书中讨论。有关参考,请参见以下内容
[1]:
import statsmodels.api as sm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from io import StringIO
原始数据,以百分比表示。我们将除以 100 以获得比例。
[2]:
raw = StringIO(
"""0.05,0.00,1.25,2.50,5.50,1.00,5.00,5.00,17.50
0.00,0.05,1.25,0.50,1.00,5.00,0.10,10.00,25.00
0.00,0.05,2.50,0.01,6.00,5.00,5.00,5.00,42.50
0.10,0.30,16.60,3.00,1.10,5.00,5.00,5.00,50.00
0.25,0.75,2.50,2.50,2.50,5.00,50.00,25.00,37.50
0.05,0.30,2.50,0.01,8.00,5.00,10.00,75.00,95.00
0.50,3.00,0.00,25.00,16.50,10.00,50.00,50.00,62.50
1.30,7.50,20.00,55.00,29.50,5.00,25.00,75.00,95.00
1.50,1.00,37.50,5.00,20.00,50.00,50.00,75.00,95.00
1.50,12.70,26.25,40.00,43.50,75.00,75.00,75.00,95.00"""
)
回归模型是一个具有站点和品种效应的双向加性模型。数据是具有 10 行(站点)和 9 列(品种)的完全无重复设计。
[3]:
df = pd.read_csv(raw, header=None)
df = df.melt()
df["site"] = 1 + np.floor(df.index / 10).astype(int)
df["variety"] = 1 + (df.index % 10)
df = df.rename(columns={"value": "blotch"})
df = df.drop("variable", axis=1)
df["blotch"] /= 100
使用标准方差函数拟合拟二项式回归。
[4]:
model1 = sm.GLM.from_formula(
"blotch ~ 0 + C(variety) + C(site)", family=sm.families.Binomial(), data=df
)
result1 = model1.fit(scale="X2")
print(result1.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: blotch No. Observations: 90
Model: GLM Df Residuals: 72
Model Family: Binomial Df Model: 17
Link Function: Logit Scale: 0.088778
Method: IRLS Log-Likelihood: -20.791
Date: Thu, 03 Oct 2024 Deviance: 6.1260
Time: 15:58:09 Pearson chi2: 6.39
No. Iterations: 10 Pseudo R-squ. (CS): 0.3198
Covariance Type: nonrobust
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
C(variety)[1] -8.0546 1.422 -5.664 0.000 -10.842 -5.268
C(variety)[2] -7.9046 1.412 -5.599 0.000 -10.672 -5.138
C(variety)[3] -7.3652 1.384 -5.321 0.000 -10.078 -4.652
C(variety)[4] -7.0065 1.372 -5.109 0.000 -9.695 -4.318
C(variety)[5] -6.4399 1.357 -4.746 0.000 -9.100 -3.780
C(variety)[6] -5.6835 1.344 -4.230 0.000 -8.317 -3.050
C(variety)[7] -5.4841 1.341 -4.090 0.000 -8.112 -2.856
C(variety)[8] -4.7126 1.331 -3.539 0.000 -7.322 -2.103
C(variety)[9] -4.5546 1.330 -3.425 0.001 -7.161 -1.948
C(variety)[10] -3.8016 1.320 -2.881 0.004 -6.388 -1.215
C(site)[T.2] 1.6391 1.443 1.136 0.256 -1.190 4.468
C(site)[T.3] 3.3265 1.349 2.466 0.014 0.682 5.971
C(site)[T.4] 3.5822 1.344 2.664 0.008 0.947 6.217
C(site)[T.5] 3.5831 1.344 2.665 0.008 0.948 6.218
C(site)[T.6] 3.8933 1.340 2.905 0.004 1.266 6.520
C(site)[T.7] 4.7300 1.335 3.544 0.000 2.114 7.346
C(site)[T.8] 5.5227 1.335 4.138 0.000 2.907 8.139
C(site)[T.9] 6.7946 1.341 5.068 0.000 4.167 9.422
==================================================================================
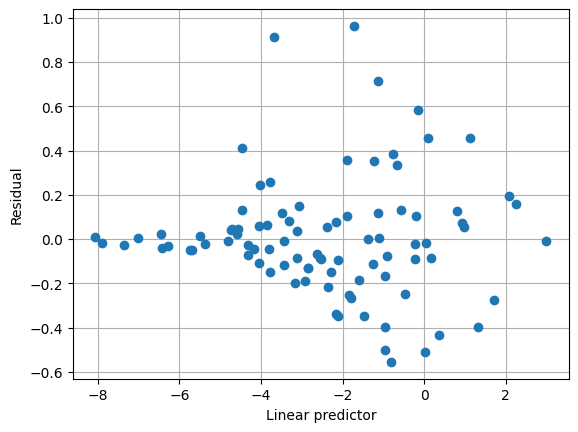
下面的图显示默认方差函数没有很好地捕获方差结构。还要注意,尺度参数估计值很小。
[5]:
plt.clf()
plt.grid(True)
plt.plot(result1.predict(linear=True), result1.resid_pearson, "o")
plt.xlabel("Linear predictor")
plt.ylabel("Residual")
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/genmod/generalized_linear_model.py:985: FutureWarning: linear keyword is deprecated, use which="linear"
warnings.warn(msg, FutureWarning)
[5]:
Text(0, 0.5, 'Residual')
另一种方差函数是 mu^2 * (1 - mu)^2。
[6]:
class vf(sm.families.varfuncs.VarianceFunction):
def __call__(self, mu):
return mu ** 2 * (1 - mu) ** 2
def deriv(self, mu):
return 2 * mu - 6 * mu ** 2 + 4 * mu ** 3
使用替代方差函数拟合拟二项式回归。
[7]:
bin = sm.families.Binomial()
bin.variance = vf()
model2 = sm.GLM.from_formula("blotch ~ 0 + C(variety) + C(site)", family=bin, data=df)
result2 = model2.fit(scale="X2")
print(result2.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: blotch No. Observations: 90
Model: GLM Df Residuals: 72
Model Family: Binomial Df Model: 17
Link Function: Logit Scale: 0.98855
Method: IRLS Log-Likelihood: -21.335
Date: Thu, 03 Oct 2024 Deviance: 7.2134
Time: 15:58:10 Pearson chi2: 71.2
No. Iterations: 25 Pseudo R-squ. (CS): 0.3115
Covariance Type: nonrobust
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
C(variety)[1] -7.9224 0.445 -17.817 0.000 -8.794 -7.051
C(variety)[2] -8.3897 0.445 -18.868 0.000 -9.261 -7.518
C(variety)[3] -7.8436 0.445 -17.640 0.000 -8.715 -6.972
C(variety)[4] -6.9683 0.445 -15.672 0.000 -7.840 -6.097
C(variety)[5] -6.5697 0.445 -14.775 0.000 -7.441 -5.698
C(variety)[6] -6.5938 0.445 -14.829 0.000 -7.465 -5.722
C(variety)[7] -5.5823 0.445 -12.555 0.000 -6.454 -4.711
C(variety)[8] -4.6598 0.445 -10.480 0.000 -5.531 -3.788
C(variety)[9] -4.7869 0.445 -10.766 0.000 -5.658 -3.915
C(variety)[10] -4.0351 0.445 -9.075 0.000 -4.907 -3.164
C(site)[T.2] 1.3831 0.445 3.111 0.002 0.512 2.255
C(site)[T.3] 3.8601 0.445 8.681 0.000 2.989 4.732
C(site)[T.4] 3.5570 0.445 8.000 0.000 2.686 4.428
C(site)[T.5] 4.1079 0.445 9.239 0.000 3.236 4.979
C(site)[T.6] 4.3054 0.445 9.683 0.000 3.434 5.177
C(site)[T.7] 4.9181 0.445 11.061 0.000 4.047 5.790
C(site)[T.8] 5.6949 0.445 12.808 0.000 4.823 6.566
C(site)[T.9] 7.0676 0.445 15.895 0.000 6.196 7.939
==================================================================================
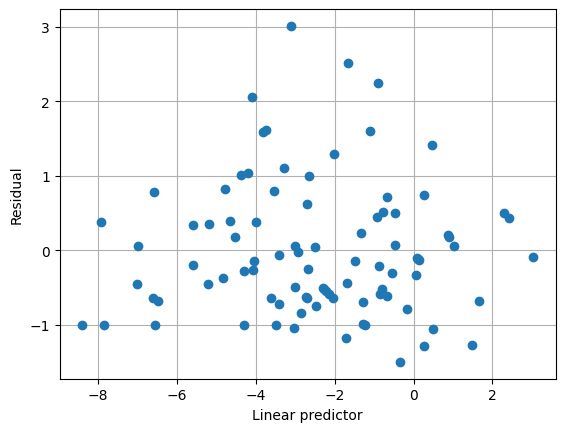
使用替代方差函数,均值/方差关系似乎很好地捕获了数据,并且估计的尺度参数接近 1。
[8]:
plt.clf()
plt.grid(True)
plt.plot(result2.predict(linear=True), result2.resid_pearson, "o")
plt.xlabel("Linear predictor")
plt.ylabel("Residual")
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/genmod/generalized_linear_model.py:985: FutureWarning: linear keyword is deprecated, use which="linear"
warnings.warn(msg, FutureWarning)
[8]:
Text(0, 0.5, 'Residual')
上次更新:2024 年 10 月 3 日