状态空间模型 - Chandrasekhar 递归¶

[1]:

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

from pandas_datareader.data import DataReader

虽然大多数与状态空间模型相关的操作依赖于卡尔曼滤波递归，但在某些特殊情况下，可以使用一种称为“Chandrasekhar 递归”的单独方法。这些提供了一种迭代计算状态向量条件矩的替代方法，在某些情况下，它们在计算量上可能比卡尔曼滤波递归少得多。有关完整详细信息，请参阅论文“使用‘Chandrasekhar 递归’评估 DSGE 模型的似然”（Herbst，2015）。这里我们只概述基本思想。

状态空间模型和卡尔曼滤波器¶

回想一下，时间不变状态空间模型可以写成

其中 \(y_t\) 是一个 \(p \times 1\) 向量，而 \(\alpha_t\) 是一个 \(m \times 1\) 向量。

卡尔曼滤波器中的每次迭代，例如在时间 \(t\)，可以分为三个部分

1. 初始化：指定 \(a_t\) 和 \(P_t\)，它们定义了条件状态分布，\(\alpha_t \mid y^{t-1} \sim N(a_t, P_t)\)。

2. 更新：计算 \(a_{t|t}\) 和 \(P_{t|t}\)，它们定义了条件状态分布，\(\alpha_t \mid y^{t} \sim N(a_{t|t}, P_{t|t})\)。

3. 预测：计算 \(a_{t+1}\) 和 \(P_{t+1}\)，它们定义了条件状态分布，\(\alpha_{t+1} \mid y^{t} \sim N(a_{t+1}, P_{t+1})\)。

当然，在第一次迭代之后，预测部分提供了下一阶段初始化所需的值。

专注于预测步骤，卡尔曼滤波递归产生

其中矩阵 \(T\) 和 \(P_{t|t}\) 都是 \(m \times m\)，其中 \(m\) 是状态向量 \(\alpha\) 的大小。在某些情况下，状态向量会变得非常大，这意味着生成 \(P_{t+1}\) 所需的矩阵乘法可能会变得计算量很大。

示例：季节性自回归¶

例如，注意 AR(r) 模型（我们在这里使用 \(r\)，因为我们已经使用 \(p\) 作为观察向量的维数）可以写成状态空间形式

其中

在具有每日数据的 AR 模型中，该模型表现出年度季节性，我们可能希望拟合一个包含高达 \(r=365\) 的滞后的模型，在这种情况下，状态向量至少为 \(m = 365\)。然后矩阵 \(T\) 和 \(P_{t|t}\) 都有 \(365^2 = 133225\) 个元素，因此计算似然函数（通过卡尔曼滤波器）所花费的大部分时间可能会被预测步骤中的矩阵乘法所支配。

状态空间模型和 Chandrasekhar 递归¶

Chandrasekhar 递归用不同的递归替换了方程 \(P_{t+1} = T P_{t|t} T' + R Q R'\)

但其中 \(W_t\) 是一个维数为 \(m \times p\) 的矩阵，而 \(M_t\) 是一个维数为 \(p \times p\) 的矩阵，其中 \(p\) 是观察向量 \(y_t\) 的维数。这些矩阵本身也具有递归公式。有关更一般的详细信息以及计算 \(W_t\) 和 \(M_t\) 的公式，请参见 Herbst (2015)。

重要说明：与卡尔曼滤波器不同，Chandrasekhar 递归不能用于所有状态空间模型。特别是，后者具有以下限制（对前者的使用没有要求）

• 该模型必须是时间不变的，但允许时间变化的截距。

• 必须使用状态向量的平稳初始化（这排除了所有非平稳分量模型）

• 不允许缺失数据

为了理解为什么这个公式可能意味着更有效的计算，再次考虑上面的 SARIMAX 案例。在这种情况下，\(p = 1\)，因此 \(M_t\) 是一个标量，我们可以将 Chandrasekhar 递归改写为

相乘的矩阵，\(W_t\)，然后是维数为 \(m \times 1\)，在 \(r=365\) 的情况下，它们每个只有 \(365\) 个元素，而不是 \(365^2\) 个元素。这意味着完成预测步骤所需的计算量要少得多。

收敛¶

一个使对性能影响的直接讨论复杂化的因素是众所周知的事实，即在时间不变模型中，预测状态协方差矩阵将收敛到一个常数矩阵。这意味着存在一个 \(S\)，使得对于每个 \(t > S\)，\(P_t = P_{t+1}\)。一旦达到收敛，我们可以完全从预测步骤中消除 \(P_{t+1}\) 的方程。

在简单的时序模型中，如 AR(r) 模型，收敛速度相当快，这可能会限制使用 Chandrasekhar 递归的性能优势。Herbst (2015) 反而关注 DSGE（动态随机一般均衡）模型，这些模型通常具有较大的状态向量，并且通常需要大量的周期才能达到收敛。在这些情况下，性能提升可能非常大。

实际例子¶

作为一个实际例子，我们将考虑具有明显季节性成分的月度数据。在这种情况下，我们查看服装的通货膨胀率，如消费者价格指数所衡量。数据图表明强烈的季节性。

[2]:

cpi_apparel = DataReader('CPIAPPNS', 'fred', start='1986')
cpi_apparel.index = pd.DatetimeIndex(cpi_apparel.index, freq='MS')
inf_apparel = np.log(cpi_apparel).diff().iloc[1:] * 1200
inf_apparel.plot(figsize=(15, 5));

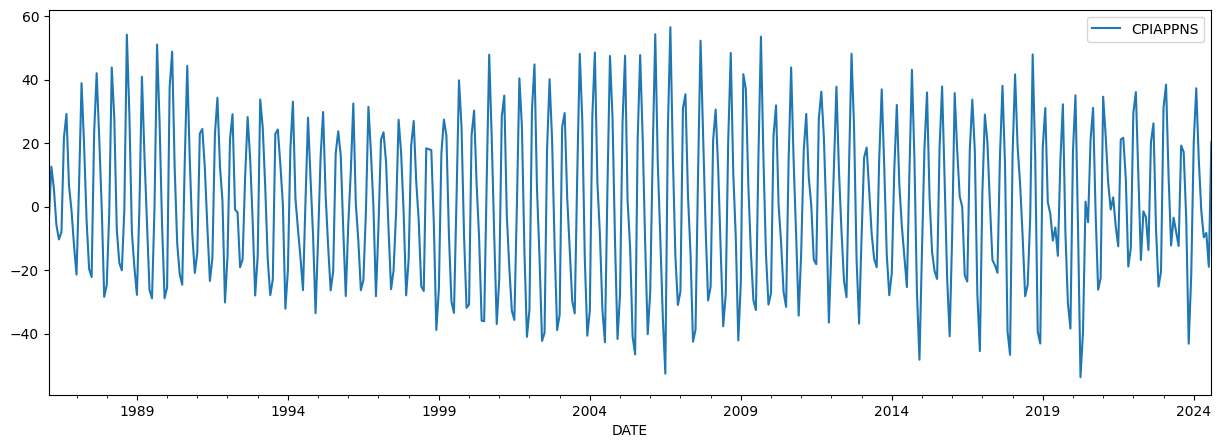
我们将构建两个模型实例。第一个将设置为使用卡尔曼滤波递归，而第二个将设置为使用 Chandrasekhar 递归。此设置由 ssm.filter_chandrasekhar 属性控制，如下所示。

我们想到的模型是一个季节性自回归，我们包括前 6 个月作为滞后，以及前 15 年中的给定月份作为滞后。这意味着状态向量具有维数 \(m = 186\)，这足够大，以至于我们可能期望通过使用 Chandrasekhar 递归来看到一些实质性的性能提升。

备注：我们在每个模型中都设置了 tolerance=0 - 这将阻止滤波器永远识别预测协方差矩阵是否已收敛。这在实践中不推荐。我们在这里这样做是为了突出显示在每个时期使用 Chandrasekhar 递归而不是典型的卡尔曼滤波递归时的出色性能。稍后，我们将展示在更现实的设置中的性能，我们允许收敛。

[3]:

# Model that will apply Kalman filter recursions
mod_kf = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12), tolerance=0)
print(mod_kf.k_states)

# Model that will apply Chandrasekhar recursions
mod_ch = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12), tolerance=0)
mod_ch.ssm.filter_chandrasekhar = True

186

我们对对数似然函数的计算时间进行计时，使用以下代码

%timeit mod_kf.loglike(mod_kf.start_params)
%timeit mod_ch.loglike(mod_ch.start_params)

这将导致

171 ms ± 19.7 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
85 ms ± 4.97 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

这意味着在这个实验中，Chandrasekhar 递归将性能提高了大约 2 倍。

正如我们上面提到的，在之前的实验中，我们禁用了预测协方差矩阵的收敛，因此那里的结果是一个上限。现在，我们按常例允许收敛，方法是删除 tolerance=0 参数

[4]:

# Model that will apply Kalman filter recursions
mod_kf = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12))
print(mod_kf.k_states)

# Model that will apply Chandrasekhar recursions
mod_ch = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12))
mod_ch.ssm.filter_chandrasekhar = True

186

再次，我们使用以下代码对对数似然函数的计算时间进行计时

%timeit mod_kf.loglike(mod_kf.start_params)
%timeit mod_ch.loglike(mod_ch.start_params)

这将导致

114 ms ± 7.64 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
70.5 ms ± 2.43 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

Chandrasekhar 递推公式仍然提高了性能，但现在仅提高了约 33%。原因是收敛后，我们不再需要计算预测的协方差矩阵，因此在这些收敛后的周期中，两种方法的计算时间没有差异。下面我们检查收敛达成的周期

[5]:

res_kf = mod_kf.filter(mod_kf.start_params)
print('Convergence at t=%d, of T=%d total observations' %
      (res_kf.filter_results.period_converged, res_kf.nobs))

Convergence at t=186, of T=463 total observations

由于收敛发生得比较早，我们已经在超过一半的周期内避免了昂贵的矩阵乘法。

但是，如上所述，较大的 DSGE 模型可能无法在样本中的大部分或所有周期内收敛，因此我们可以预期获得与第一个示例更相似的性能提升。在他们 2019 年的论文“使用金融或劳动力市场摩擦的欧元区实时密度预测”中，McAdam 和 Warne 指出，在他们的应用中，“与标准卡尔曼滤波器相比，根据我们的经验，这些递推公式将三个模型的对数似然计算速度提高了大约 50%”。这与我们在第一个示例中发现的结果大致相同。

关于多线程矩阵代数例程¶

以上计时基于通过 Anaconda 安装的 Numpy 安装，它使用英特尔的 MKL BLAS 和 LAPACK 库。这些库实现了多线程处理以加快矩阵代数，这对于对我们在这里使用的较大矩阵的操作尤其有用。为了了解这将如何影响结果，我们可以通过在该笔记本的第一个单元格中放置以下内容来关闭多线程。

import os
os.environ["MKL_NUM_THREADS"] = "1"

当我们这样做时，第一个示例的计时更改为

307 ms ± 3.08 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
97.5 ms ± 1.64 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

第二个示例的计时更改为

178 ms ± 2.78 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
78.9 ms ± 950 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

两者都变慢了，但典型的卡尔曼滤波器的影响更大。

这并不出乎意料；单线程和多线程线性代数之间的性能差异在典型的卡尔曼滤波器情况下更大，因为 Chandrasekhar 递推公式的要点是减小矩阵运算的大小。这意味着，如果多线程线性代数不可用，Chandrasekhar 递推公式将提供更大的性能提升。

Chandrasekhar 递推公式和单变量滤波方法¶

也可以将 Chandrasekhar 递推公式与 Koopman 和 Durbin (2000) 的单变量滤波方法结合使用，方法是利用 Aknouche 和 Hamdi 在他们 2007 年的论文“周期性 Chandrasekhar 递推公式”中的结果。这种组合的初始实现包含在 Statsmodels 中。但是，实验表明，与通常的卡尔曼滤波器相比，这往往会降低性能。这与单变量滤波方法的计算节省量相符，这表明当状态向量相对于观测向量很小时，节省量最大。

参考文献¶

Aknouche，Abdelhakim 和 Fayçal Hamdi。“周期性 Chandrasekhar 递推公式。”arXiv 预印本 arXiv:0711.3857 (2007)。

Herbst，Edward。“使用“Chandrasekhar 递推公式”评估 DSGE 模型的似然函数。”计算经济学 45，第 4 期（2015）：693-705。

Koopman，Siem J. 和 James Durbin。“多变量状态空间模型的快速滤波和平滑。”时间序列分析杂志 21，第 3 期（2000）：281-296。

McAdam，Peter 和 Anders Warne。“使用金融或劳动力市场摩擦的欧元区实时密度预测。”国际预测杂志 35，第 2 期（2019）：580-600。