预测(样本外)¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
人工数据¶
[3]:
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1 - 5) ** 2))
X = sm.add_constant(X)
beta = [5.0, 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
估计¶
[4]:
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.980
Model: OLS Adj. R-squared: 0.979
Method: Least Squares F-statistic: 767.8
Date: Thu, 03 Oct 2024 Prob (F-statistic): 2.80e-39
Time: 15:50:37 Log-Likelihood: -3.6609
No. Observations: 50 AIC: 15.32
Df Residuals: 46 BIC: 22.97
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 5.0304 0.093 54.373 0.000 4.844 5.217
x1 0.5002 0.014 35.058 0.000 0.471 0.529
x2 0.5011 0.056 8.934 0.000 0.388 0.614
x3 -0.0201 0.001 -16.012 0.000 -0.023 -0.018
==============================================================================
Omnibus: 2.155 Durbin-Watson: 1.847
Prob(Omnibus): 0.340 Jarque-Bera (JB): 2.068
Skew: -0.462 Prob(JB): 0.356
Kurtosis: 2.630 Cond. No. 221.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
样本内预测¶
[5]:
ypred = olsres.predict(X)
print(ypred)
[ 4.52892208 5.01052175 5.45275967 5.82832671 6.11976948 6.32235784
6.44486207 6.50811191 6.54157432 6.57851213 6.65051904 6.7823289
6.98775197 7.26740594 7.60861448 7.98748987 8.37285773 8.73137887
9.03302681 9.25602105 9.39040558 9.43968456 9.42024665 9.35867239
9.28736706 9.23923662 9.24228135 9.31499546 9.46332857 9.67970819
9.94428385 10.2281885 10.49828128 10.72259244 10.87557591 10.94230645
10.9209318 10.82297701 10.67145093 10.49706588 10.33319174 10.21037335
10.15131209 10.1671361 10.25557197 10.40131825 10.57855941 10.75520731
10.89817315 10.97880387]
创建新的解释变量样本 Xnew,进行预测和绘图¶
[6]:
x1n = np.linspace(20.5, 25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n - 5) ** 2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
[10.96503747 10.81894524 10.56017815 10.23351824 9.89791447 9.61204991
9.4199741 9.34031818 9.36173334 9.44566941]
绘制比较图¶
[7]:
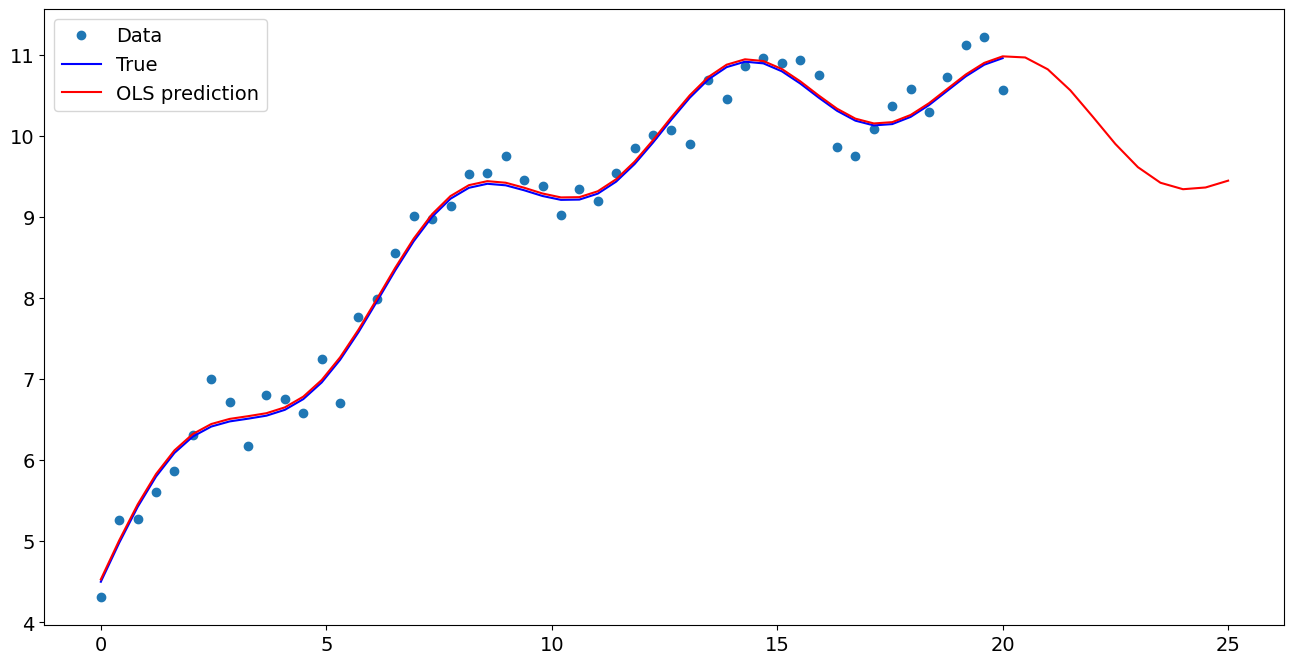
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "r", label="OLS prediction")
ax.legend(loc="best")
[7]:
<matplotlib.legend.Legend at 0x7f30514b3fd0>
使用公式进行预测¶
使用公式可以使估计和预测变得更加容易
[8]:
from statsmodels.formula.api import ols
data = {"x1": x1, "y": y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
我们使用 I 来指示使用恒等变换。也就是说,我们不想使用 **2 进行任何扩展魔法
[9]:
res.params
[9]:
Intercept 5.030411
x1 0.500216
np.sin(x1) 0.501093
I((x1 - 5) ** 2) -0.020060
dtype: float64
现在我们只需要传递单个变量,就可以自动获得变换后的右手边变量
[10]:
res.predict(exog=dict(x1=x1n))
[10]:
0 10.965037
1 10.818945
2 10.560178
3 10.233518
4 9.897914
5 9.612050
6 9.419974
7 9.340318
8 9.361733
9 9.445669
dtype: float64
最后更新:2024 年 10 月 3 日