稳健线性模型¶
[1]:
%matplotlib inline
[2]:
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
估计¶
加载数据
[3]:
data = sm.datasets.stackloss.load()
data.exog = sm.add_constant(data.exog)
使用(默认)中位数绝对偏差缩放的 Huber T 范数
[4]:
huber_t = sm.RLM(data.endog, data.exog, M=sm.robust.norms.HuberT())
hub_results = huber_t.fit()
print(hub_results.params)
print(hub_results.bse)
print(
hub_results.summary(
yname="y", xname=["var_%d" % i for i in range(len(hub_results.params))]
)
)
const -41.026498
AIRFLOW 0.829384
WATERTEMP 0.926066
ACIDCONC -0.127847
dtype: float64
const 9.791899
AIRFLOW 0.111005
WATERTEMP 0.302930
ACIDCONC 0.128650
dtype: float64
Robust linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 21
Model: RLM Df Residuals: 17
Method: IRLS Df Model: 3
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Thu, 03 Oct 2024
Time: 15:51:12
No. Iterations: 19
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
var_0 -41.0265 9.792 -4.190 0.000 -60.218 -21.835
var_1 0.8294 0.111 7.472 0.000 0.612 1.047
var_2 0.9261 0.303 3.057 0.002 0.332 1.520
var_3 -0.1278 0.129 -0.994 0.320 -0.380 0.124
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
使用 'H2' 协方差矩阵的 Huber T 范数
[5]:
hub_results2 = huber_t.fit(cov="H2")
print(hub_results2.params)
print(hub_results2.bse)
const -41.026498
AIRFLOW 0.829384
WATERTEMP 0.926066
ACIDCONC -0.127847
dtype: float64
const 9.089504
AIRFLOW 0.119460
WATERTEMP 0.322355
ACIDCONC 0.117963
dtype: float64
使用 Huber 提案 2 缩放和 'H3' 协方差矩阵的 Andrew's Wave 范数
[6]:
andrew_mod = sm.RLM(data.endog, data.exog, M=sm.robust.norms.AndrewWave())
andrew_results = andrew_mod.fit(scale_est=sm.robust.scale.HuberScale(), cov="H3")
print("Parameters: ", andrew_results.params)
Parameters: const -40.881796
AIRFLOW 0.792761
WATERTEMP 1.048576
ACIDCONC -0.133609
dtype: float64
有关更多选项,请参见 help(sm.RLM.fit),有关比例选项,请参见 module sm.robust.scale
比较 OLS 和 RLM¶
具有异常值的合成数据
[7]:
nsample = 50
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, (x1 - 5) ** 2))
X = sm.add_constant(X)
sig = 0.3 # smaller error variance makes OLS<->RLM contrast bigger
beta = [5, 0.5, -0.0]
y_true2 = np.dot(X, beta)
y2 = y_true2 + sig * 1.0 * np.random.normal(size=nsample)
y2[[39, 41, 43, 45, 48]] -= 5 # add some outliers (10% of nsample)
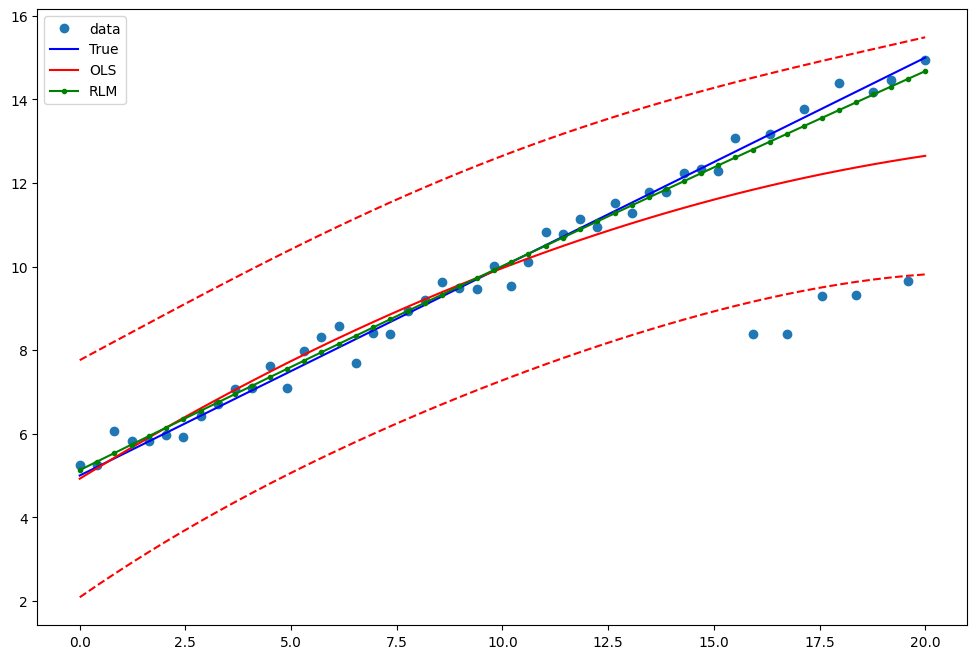
示例 1:具有线性真实值的二次函数¶
注意,OLS 回归中的二次项将捕获异常值的影响。
[8]:
res = sm.OLS(y2, X).fit()
print(res.params)
print(res.bse)
print(res.predict())
[ 5.21792383 0.50415069 -0.01178124]
[0.43595638 0.06730578 0.00595552]
[ 4.92339275 5.17529253 5.42326685 5.66731574 5.90743917 6.14363717
6.37590971 6.60425681 6.82867847 7.04917468 7.26574545 7.47839077
7.68711064 7.89190507 8.09277405 8.28971759 8.48273568 8.67182833
8.85699553 9.03823729 9.2155536 9.38894447 9.55840989 9.72394987
9.8855644 10.04325348 10.19701712 10.34685531 10.49276806 10.63475536
10.77281722 10.90695363 11.0371646 11.16345012 11.2858102 11.40424483
11.51875401 11.62933775 11.73599605 11.8387289 11.9375363 12.03241826
12.12337477 12.21040584 12.29351146 12.37269164 12.44794637 12.51927566
12.5866795 12.65015789]
估计 RLM
[9]:
resrlm = sm.RLM(y2, X).fit()
print(resrlm.params)
print(resrlm.bse)
[ 5.15683122e+00 4.88535174e-01 -1.11256925e-03]
[0.12686184 0.01958576 0.00173304]
绘制图表以比较 OLS 估计值与稳健估计值
[10]:
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
ax.plot(x1, y2, "o", label="data")
ax.plot(x1, y_true2, "b-", label="True")
pred_ols = res.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
ax.plot(x1, res.fittedvalues, "r-", label="OLS")
ax.plot(x1, iv_u, "r--")
ax.plot(x1, iv_l, "r--")
ax.plot(x1, resrlm.fittedvalues, "g.-", label="RLM")
ax.legend(loc="best")
[10]:
<matplotlib.legend.Legend at 0x7ff47df37c10>
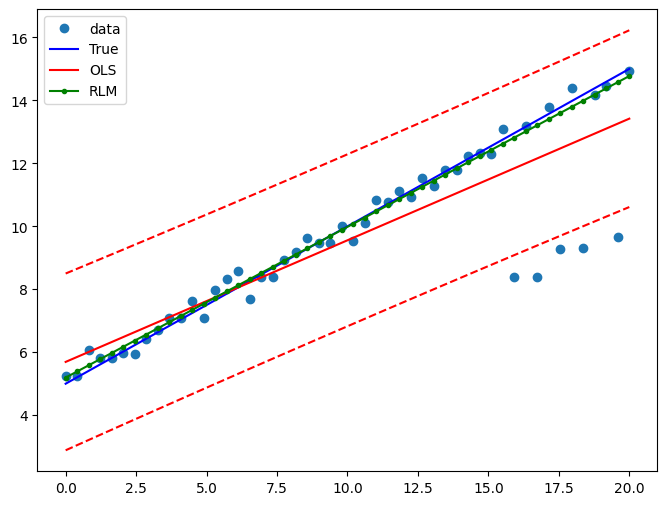
示例 2:具有线性真实值的线性函数¶
仅使用线性项和常数项拟合新的 OLS 模型
[11]:
X2 = X[:, [0, 1]]
res2 = sm.OLS(y2, X2).fit()
print(res2.params)
print(res2.bse)
[5.69278005 0.38633826]
[0.37479982 0.03229427]
估计 RLM
[12]:
resrlm2 = sm.RLM(y2, X2).fit()
print(resrlm2.params)
print(resrlm2.bse)
[5.19360532 0.47898089]
[0.10312091 0.00888531]
绘制图表以比较 OLS 估计值与稳健估计值
[13]:
pred_ols = res2.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x1, y2, "o", label="data")
ax.plot(x1, y_true2, "b-", label="True")
ax.plot(x1, res2.fittedvalues, "r-", label="OLS")
ax.plot(x1, iv_u, "r--")
ax.plot(x1, iv_l, "r--")
ax.plot(x1, resrlm2.fittedvalues, "g.-", label="RLM")
legend = ax.legend(loc="best")
最后更新:2024 年 10 月 3 日