Copula - 多元联合分布¶
[1]:
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy import stats
sns.set_style("darkgrid")
sns.mpl.rc("figure", figsize=(8, 8))
[2]:
%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
在对系统建模时,通常情况下会涉及多个参数。每个参数都可以用给定的概率密度函数 (PDF) 来描述。如果需要生成一组新的参数值,则需要能够从这些分布中采样,这些分布也被称为边缘分布。主要有两种情况:(i) PDF 是独立的;(ii) 存在依赖关系。对依赖关系进行建模的一种方法是使用 **copula**。
从 Copula 采样¶
让我们使用一个双变量示例,并首先假设我们有一个先验,并且知道如何对 2 个变量之间的依赖关系进行建模。
在本例中,我们使用 Gumbel Copula 并将其超参数 theta=2 固定。我们可以将其 2 维 PDF 可视化。
[3]:
from statsmodels.distributions.copula.api import (
CopulaDistribution, GumbelCopula, IndependenceCopula)
copula = GumbelCopula(theta=2)
_ = copula.plot_pdf() # returns a matplotlib figure
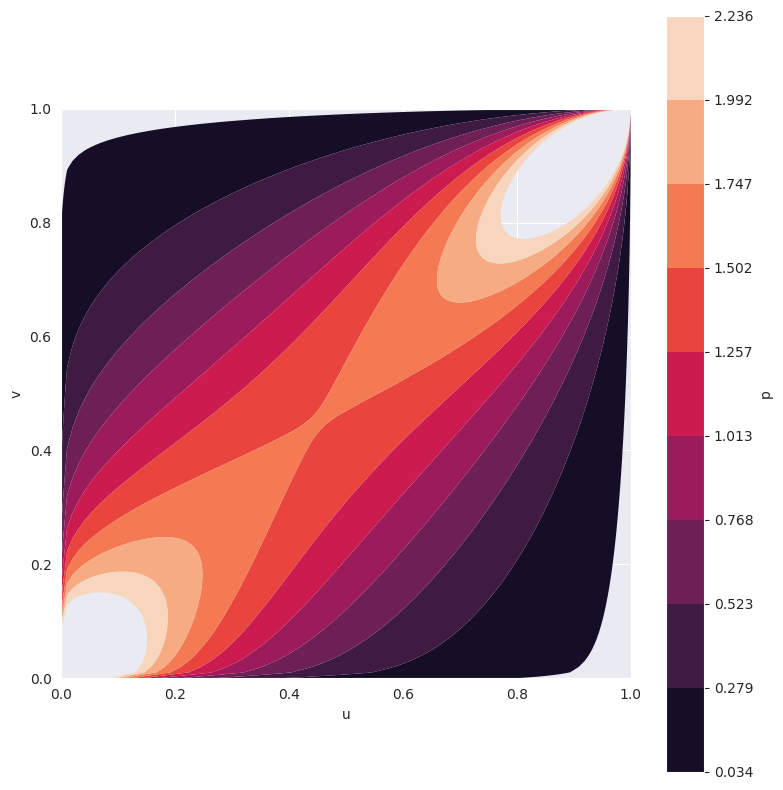
我们可以对 PDF 进行采样。
[4]:
sample = copula.rvs(10000)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="hex")
_ = h.set_axis_labels("X1", "X2", fontsize=16)
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tools/rng_qrng.py:54: FutureWarning: Passing `None` as the seed currently return the NumPy singleton RandomState
(np.random.mtrand._rand). After release 0.13 this will change to using the
default generator provided by NumPy (np.random.default_rng()). If you need
reproducible draws, you should pass a seeded np.random.Generator, e.g.,
import numpy as np
seed = 32839283923801
rng = np.random.default_rng(seed)"
warnings.warn(_future_warn, FutureWarning)
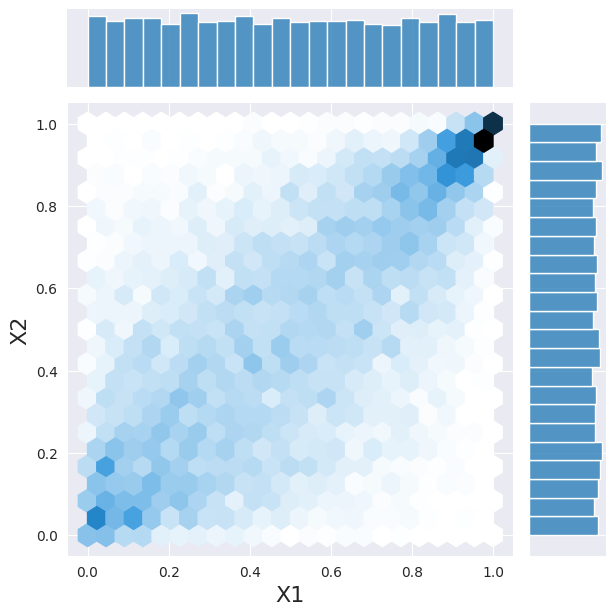
让我们回到我们的 2 个变量。在本例中,我们认为它们是伽马分布和正态分布。如果它们相互独立,我们可以分别从每个 PDF 中采样。这里我们使用一个方便的类来执行相同的操作。
可重复性¶
从 Copula 生成可重复的随机值需要显式设置 seed 参数。 seed 接受已初始化的 NumPy Generator 或 RandomState,或任何可接受的 np.random.default_rng 参数,例如,整数或整数序列。本示例使用整数。
在 np.random 分布中直接公开的单例 RandomState 未被使用,并且设置 np.random.seed 对生成的值没有影响。
[5]:
marginals = [stats.gamma(2), stats.norm]
joint_dist = CopulaDistribution(copula=IndependenceCopula(), marginals=marginals)
sample = joint_dist.rvs(512, random_state=20210801)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="scatter")
_ = h.set_axis_labels("X1", "X2", fontsize=16)
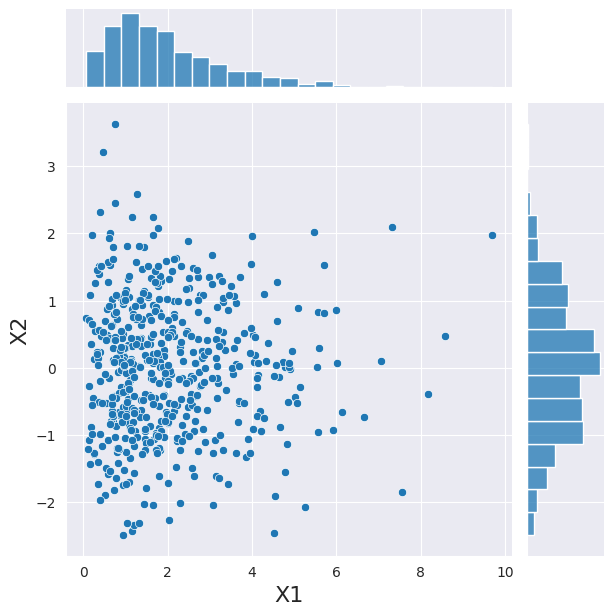
现在,我们在上面使用 Copula 表达了变量之间的依赖关系,我们可以使用此 Copula 来使用相同的便捷类采样一组新的观测值。
[6]:
joint_dist = CopulaDistribution(copula, marginals)
# Use an initialized Generator object
rng = np.random.default_rng([2, 0, 2, 1, 0, 8, 0, 1])
sample = joint_dist.rvs(512, random_state=rng)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="scatter")
_ = h.set_axis_labels("X1", "X2", fontsize=16)
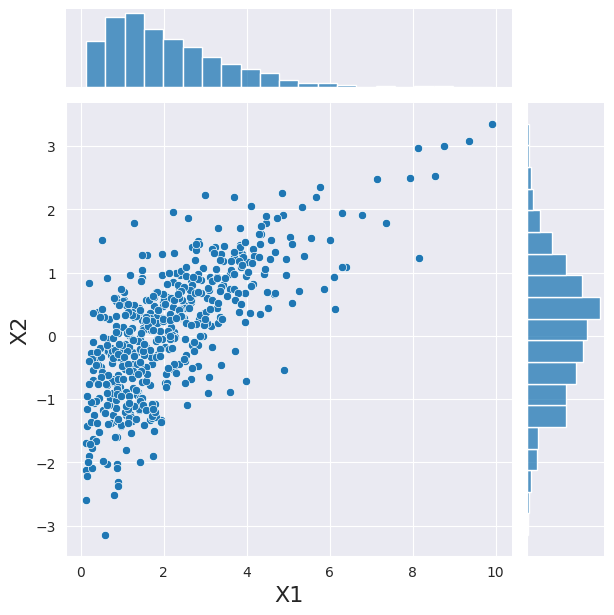
这里需要注意两点。(i) 与独立情况一样,边缘分布正确地显示了伽马分布和正态分布;(ii) 两个变量之间存在依赖关系。
估计 Copula 参数¶
现在,假设我们已经拥有实验数据,并且知道存在一个可以用 Gumbel Copula 表达的依赖关系。但我们不知道 Copula 的超参数值是什么。在这种情况下,我们可以估计该值。
我们将使用我们刚刚生成的样本,因为我们已经知道应该获得的超参数值: theta=2。
[7]:
copula = GumbelCopula()
theta = copula.fit_corr_param(sample)
print(theta)
2.049379621506455
我们可以看到,估计的超参数值接近先前设置的值。