自回归¶

本笔记本介绍了使用 AutoReg 模型进行自回归建模。它还涵盖了 ar_select_order 的方面，该方面有助于选择最小化信息准则（如 AIC）的模型。自回归模型的动态由下式给出

\[y_t = \delta + \phi_1 y_{t-1} + \ldots + \phi_p y_{t-p} + \epsilon_t.\]

AutoReg 还允许具有以下模型

确定性项 (trend)
- n: 无确定性项
- c: 常数（默认）
- ct: 常数和时间趋势
- t: 仅时间趋势
季节性虚拟变量 (seasonal)
- True 包含 \(s-1\) 个虚拟变量，其中 \(s\) 是时间序列的周期（例如，对于月度数据为 12）
自定义确定性项 (deterministic)
- 接受 DeterministicProcess
外生变量 (exog)
- 包含在模型中的外生变量的 DataFrame 或 array
省略选定的滞后 (lags)
- 如果 lags 是整数的迭代器，则仅包含这些滞后在模型中。

完整规范为

\[y_t = \delta_0 + \delta_1 t + \phi_1 y_{t-1} + \ldots + \phi_p y_{t-p} + \sum_{i=1}^{s-1} \gamma_i d_i + \sum_{j=1}^{m} \kappa_j x_{t,j} + \epsilon_t.\]

其中

\(d_i\) 是一个季节性虚拟变量，如果 \(mod(t, period) = i\) 则为 1。如果模型包含常数 (c 在 trend 中)，则排除周期 0。
\(t\) 是一个时间趋势 (\(1,2,\ldots\))，从第一个观测值的 1 开始。
\(x_{t,j}\) 是外生回归量。**注意** 在定义模型时，这些回归量与左侧变量的时间对齐。
\(\epsilon_t\) 假设为白噪声过程。

第一个单元格导入标准包并将绘图设置为内联显示。

[1]:

%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
from statsmodels.tsa.api import acf, graphics, pacf
from statsmodels.tsa.ar_model import AutoReg, ar_select_order

此单元格设置绘图样式，为 matplotlib 注册 pandas 日期转换器，并设置默认图形大小。

[2]:

sns.set_style("darkgrid")
pd.plotting.register_matplotlib_converters()
# Default figure size
sns.mpl.rc("figure", figsize=(16, 6))
sns.mpl.rc("font", size=14)

第一组示例使用美国房屋开工数量的环比增长率，该增长率未经季节性调整。季节性通过规律的峰值和谷值模式明显。我们将时间序列的频率设置为“MS”（月开始）以避免在使用 AutoReg 时出现警告。

[3]:

data = pdr.get_data_fred("HOUSTNSA", "1959-01-01", "2019-06-01")
housing = data.HOUSTNSA.pct_change().dropna()
# Scale by 100 to get percentages
housing = 100 * housing.asfreq("MS")
fig, ax = plt.subplots()
ax = housing.plot(ax=ax)

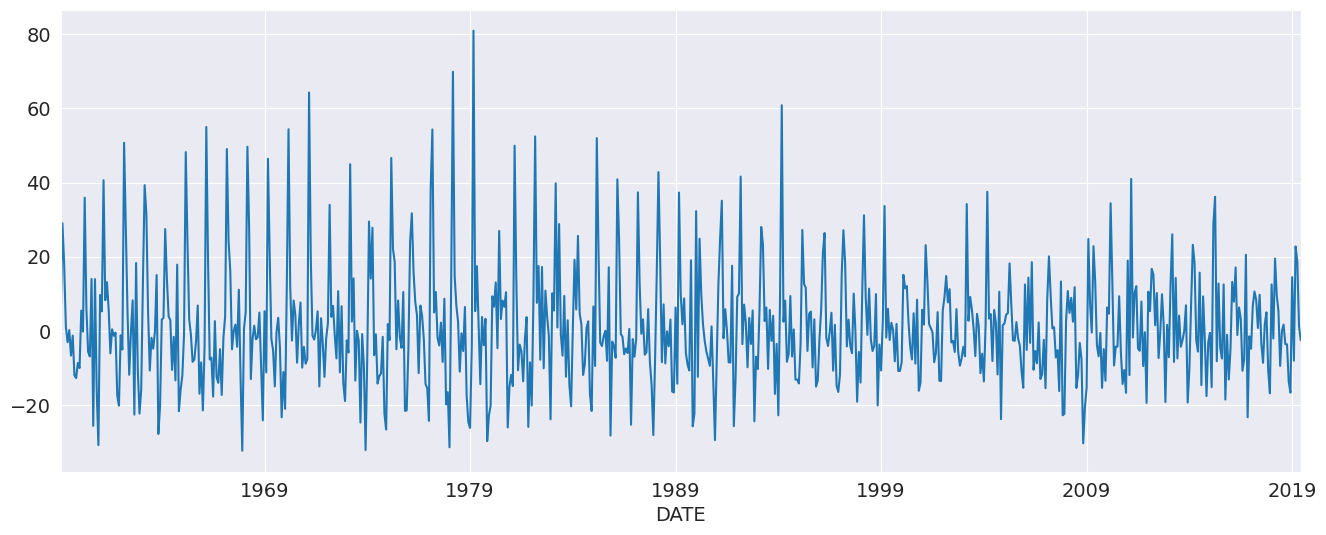
../../../_images/examples_notebooks_generated_autoregressions_6_0.png

我们可以从 AR(3) 开始。虽然这对这些数据不是一个好的模型，但它展示了 API 的基本用法。

[4]:

mod = AutoReg(housing, 3, old_names=False)
res = mod.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  725
Model:                     AutoReg(3)   Log Likelihood               -2993.442
Method:               Conditional MLE   S.D. of innovations             15.289
Date:                Thu, 03 Oct 2024   AIC                           5996.884
Time:                        15:55:21   BIC                           6019.794
Sample:                    05-01-1959   HQIC                          6005.727
                         - 06-01-2019
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
const           1.1228      0.573      1.961      0.050       0.000       2.245
HOUSTNSA.L1     0.1910      0.036      5.235      0.000       0.120       0.263
HOUSTNSA.L2     0.0058      0.037      0.155      0.877      -0.067       0.079
HOUSTNSA.L3    -0.1939      0.036     -5.319      0.000      -0.265      -0.122
                                    Roots
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            0.9680           -1.3298j            1.6448           -0.1499
AR.2            0.9680           +1.3298j            1.6448            0.1499
AR.3           -1.9064           -0.0000j            1.9064           -0.5000
-----------------------------------------------------------------------------

AutoReg 支持与 OLS 相同的协方差估计器。在下文中，我们使用 cov_type="HC0"，即怀特协方差估计器。虽然参数估计值相同，但所有依赖于标准误差的数量都会发生变化。

[5]:

res = mod.fit(cov_type="HC0")
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  725
Model:                     AutoReg(3)   Log Likelihood               -2993.442
Method:               Conditional MLE   S.D. of innovations             15.289
Date:                Thu, 03 Oct 2024   AIC                           5996.884
Time:                        15:55:21   BIC                           6019.794
Sample:                    05-01-1959   HQIC                          6005.727
                         - 06-01-2019
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
const           1.1228      0.601      1.869      0.062      -0.055       2.300
HOUSTNSA.L1     0.1910      0.035      5.499      0.000       0.123       0.259
HOUSTNSA.L2     0.0058      0.039      0.150      0.881      -0.070       0.081
HOUSTNSA.L3    -0.1939      0.036     -5.448      0.000      -0.264      -0.124
                                    Roots
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            0.9680           -1.3298j            1.6448           -0.1499
AR.2            0.9680           +1.3298j            1.6448            0.1499
AR.3           -1.9064           -0.0000j            1.9064           -0.5000
-----------------------------------------------------------------------------

[6]:

sel = ar_select_order(housing, 13, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  725
Model:                    AutoReg(13)   Log Likelihood               -2676.157
Method:               Conditional MLE   S.D. of innovations             10.378
Date:                Thu, 03 Oct 2024   AIC                           5382.314
Time:                        15:55:21   BIC                           5450.835
Sample:                    03-01-1960   HQIC                          5408.781
                         - 06-01-2019
================================================================================
                   coef    std err          z      P>|z|      [0.025      0.975]
--------------------------------------------------------------------------------
const            1.3615      0.458      2.970      0.003       0.463       2.260
HOUSTNSA.L1     -0.2900      0.036     -8.161      0.000      -0.360      -0.220
HOUSTNSA.L2     -0.0828      0.031     -2.652      0.008      -0.144      -0.022
HOUSTNSA.L3     -0.0654      0.031     -2.106      0.035      -0.126      -0.005
HOUSTNSA.L4     -0.1596      0.031     -5.166      0.000      -0.220      -0.099
HOUSTNSA.L5     -0.0434      0.031     -1.387      0.165      -0.105       0.018
HOUSTNSA.L6     -0.0884      0.031     -2.867      0.004      -0.149      -0.028
HOUSTNSA.L7     -0.0556      0.031     -1.797      0.072      -0.116       0.005
HOUSTNSA.L8     -0.1482      0.031     -4.803      0.000      -0.209      -0.088
HOUSTNSA.L9     -0.0926      0.031     -2.960      0.003      -0.154      -0.031
HOUSTNSA.L10    -0.1133      0.031     -3.665      0.000      -0.174      -0.053
HOUSTNSA.L11     0.1151      0.031      3.699      0.000       0.054       0.176
HOUSTNSA.L12     0.5352      0.031     17.133      0.000       0.474       0.596
HOUSTNSA.L13     0.3178      0.036      8.937      0.000       0.248       0.388
                                    Roots
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1             1.0913           -0.0000j            1.0913           -0.0000
AR.2             0.8743           -0.5018j            1.0080           -0.0829
AR.3             0.8743           +0.5018j            1.0080            0.0829
AR.4             0.5041           -0.8765j            1.0111           -0.1669
AR.5             0.5041           +0.8765j            1.0111            0.1669
AR.6             0.0056           -1.0530j            1.0530           -0.2491
AR.7             0.0056           +1.0530j            1.0530            0.2491
AR.8            -0.5263           -0.9335j            1.0716           -0.3317
AR.9            -0.5263           +0.9335j            1.0716            0.3317
AR.10           -0.9525           -0.5880j            1.1194           -0.4120
AR.11           -0.9525           +0.5880j            1.1194            0.4120
AR.12           -1.2928           -0.2608j            1.3189           -0.4683
AR.13           -1.2928           +0.2608j            1.3189            0.4683
------------------------------------------------------------------------------

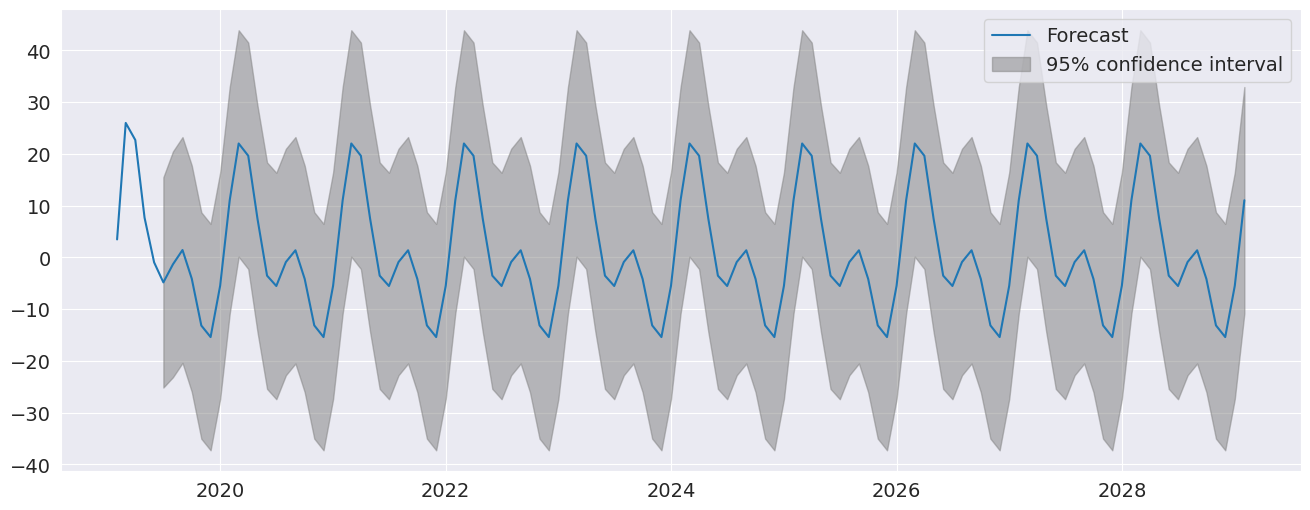
plot_predict 可视化预测。在这里，我们生成大量预测，这些预测显示了模型捕获的强季节性。

[7]:

fig = res.plot_predict(720, 840)

../../../_images/examples_notebooks_generated_autoregressions_13_0.png

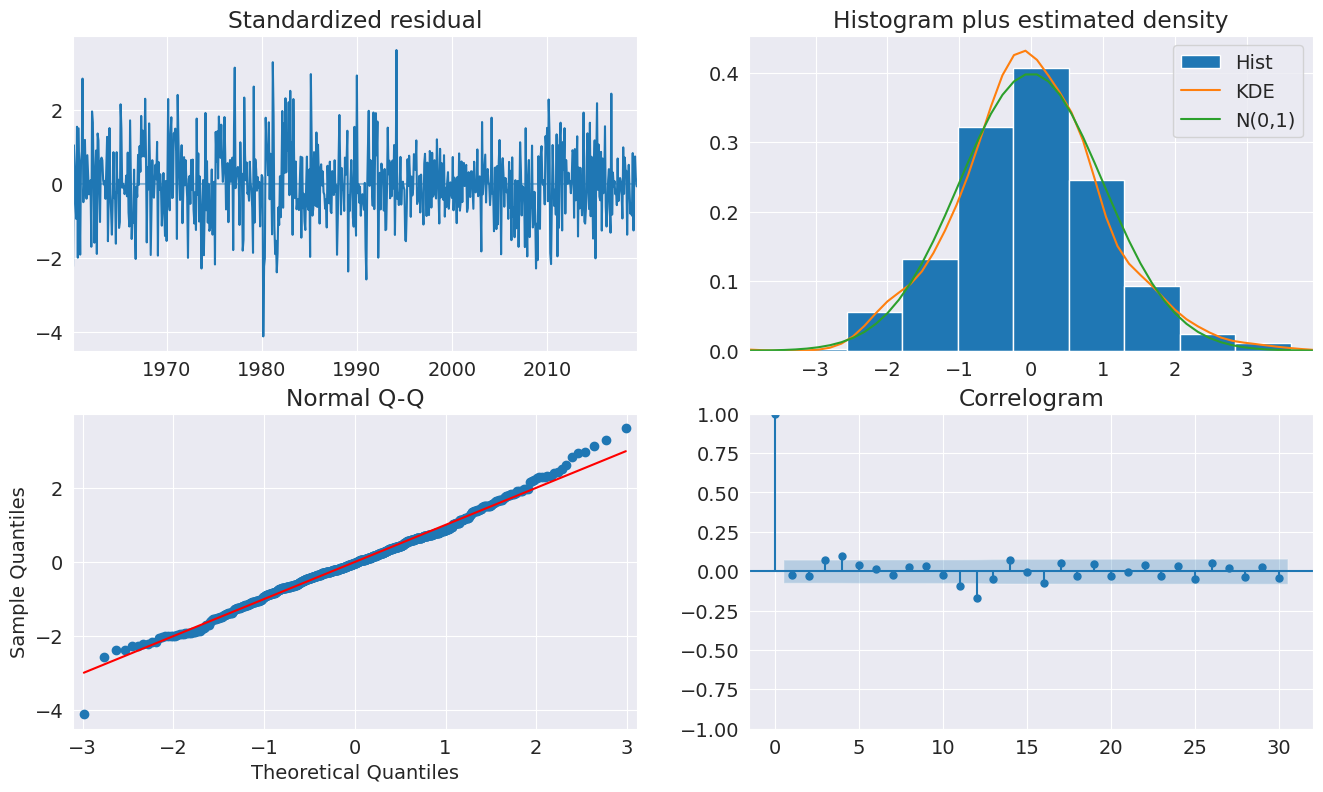
plot_diagnositcs 表明该模型捕获了数据中的关键特征。

[8]:

fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)

../../../_images/examples_notebooks_generated_autoregressions_15_0.png

季节性虚拟变量¶

AutoReg 支持季节性虚拟变量，这是对季节性建模的另一种方法。包含虚拟变量将动态缩短为仅 AR(2)。

[9]:

sel = ar_select_order(housing, 13, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  725
Model:               Seas. AutoReg(2)   Log Likelihood               -2652.556
Method:               Conditional MLE   S.D. of innovations              9.487
Date:                Thu, 03 Oct 2024   AIC                           5335.112
Time:                        15:55:27   BIC                           5403.863
Sample:                    04-01-1959   HQIC                          5361.648
                         - 06-01-2019
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
const           1.2726      1.373      0.927      0.354      -1.418       3.963
s(2,12)        32.6477      1.824     17.901      0.000      29.073      36.222
s(3,12)        23.0685      2.435      9.472      0.000      18.295      27.842
s(4,12)        10.7267      2.693      3.983      0.000       5.449      16.005
s(5,12)         1.6792      2.100      0.799      0.424      -2.437       5.796
s(6,12)        -4.4229      1.896     -2.333      0.020      -8.138      -0.707
s(7,12)        -4.2113      1.824     -2.309      0.021      -7.786      -0.636
s(8,12)        -6.4124      1.791     -3.581      0.000      -9.922      -2.902
s(9,12)         0.1095      1.800      0.061      0.952      -3.419       3.638
s(10,12)      -16.7511      1.814     -9.234      0.000     -20.307     -13.196
s(11,12)      -20.7023      1.862    -11.117      0.000     -24.352     -17.053
s(12,12)      -11.9554      1.778     -6.724      0.000     -15.440      -8.470
HOUSTNSA.L1    -0.2953      0.037     -7.994      0.000      -0.368      -0.223
HOUSTNSA.L2    -0.1148      0.037     -3.107      0.002      -0.187      -0.042
                                    Roots
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1           -1.2862           -2.6564j            2.9514           -0.3218
AR.2           -1.2862           +2.6564j            2.9514            0.3218
-----------------------------------------------------------------------------

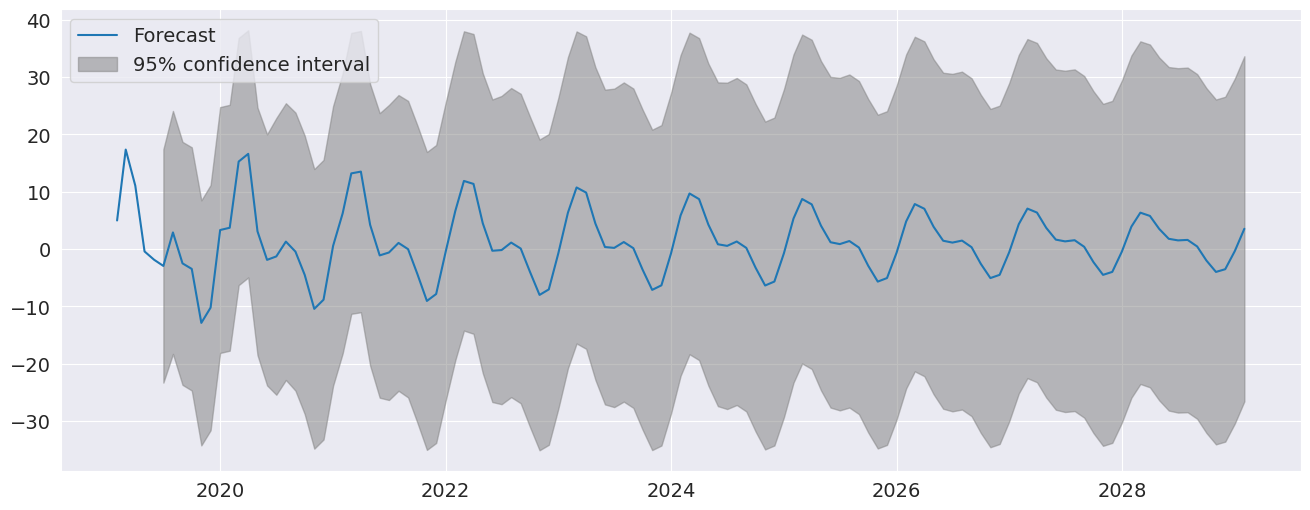
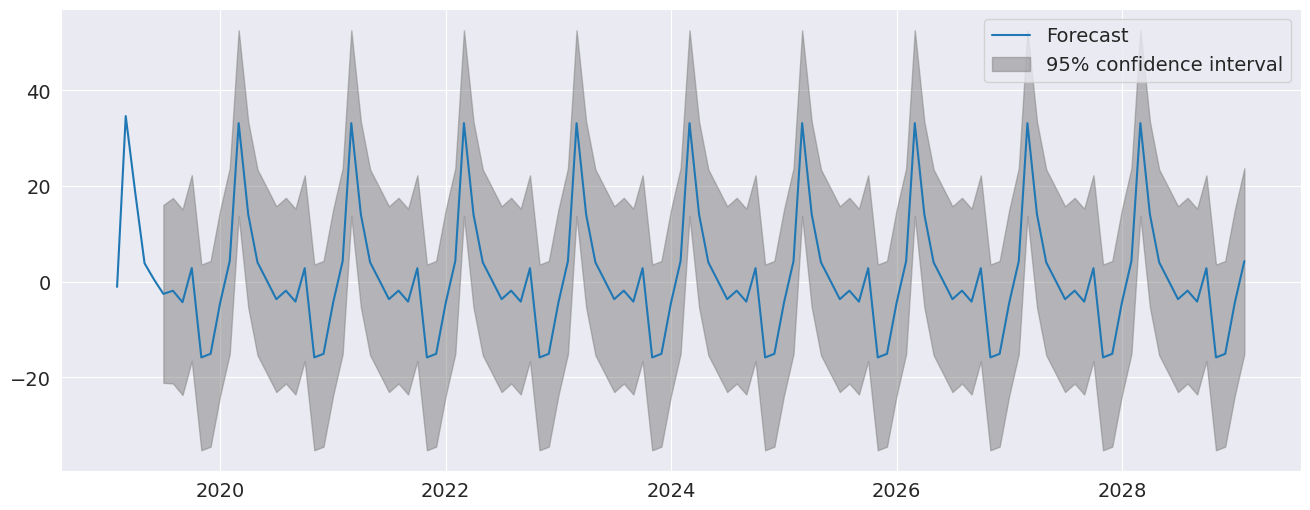
季节性虚拟变量在预测中很明显，预测在未来 10 年的每个周期中都有一个非平凡的季节性分量。

[10]:

fig = res.plot_predict(720, 840)

../../../_images/examples_notebooks_generated_autoregressions_20_0.png

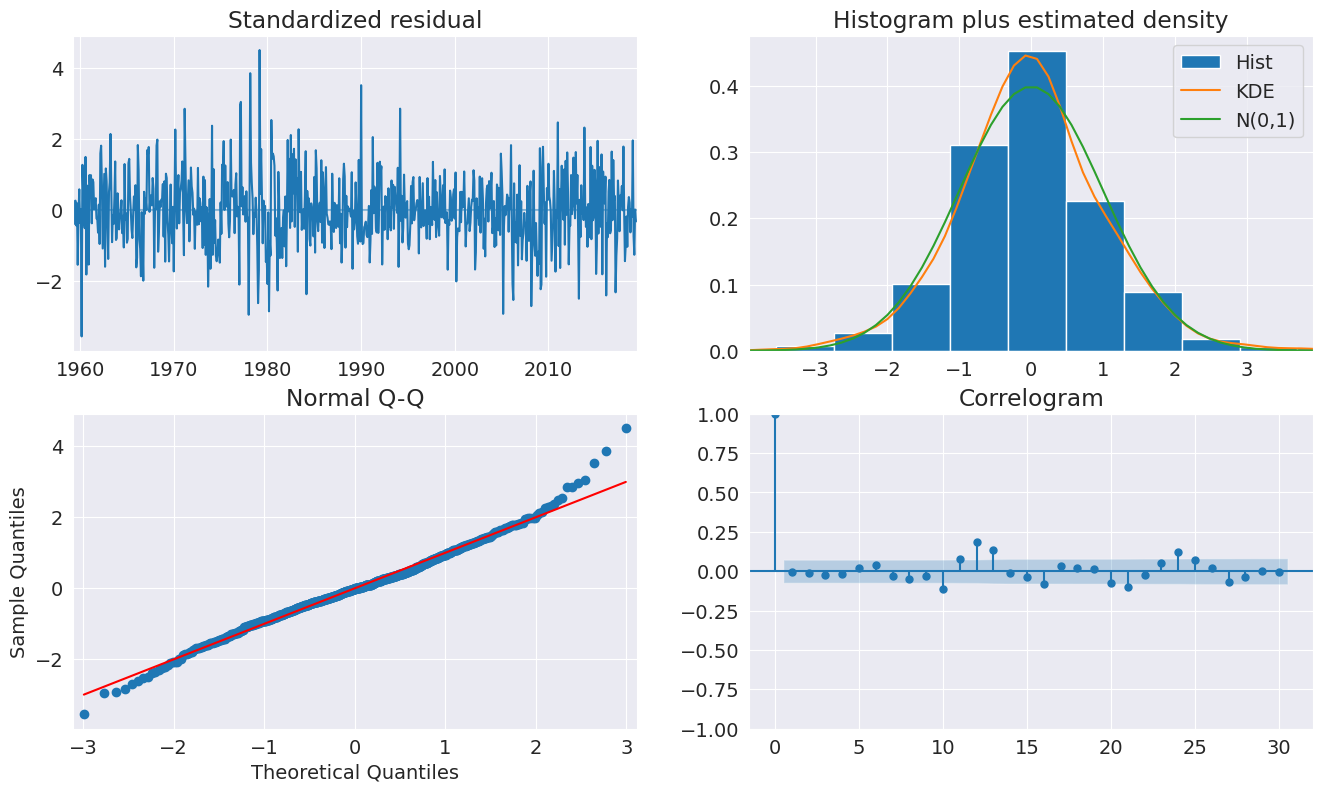
[11]:

fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(lags=30, fig=fig)

../../../_images/examples_notebooks_generated_autoregressions_21_0.png

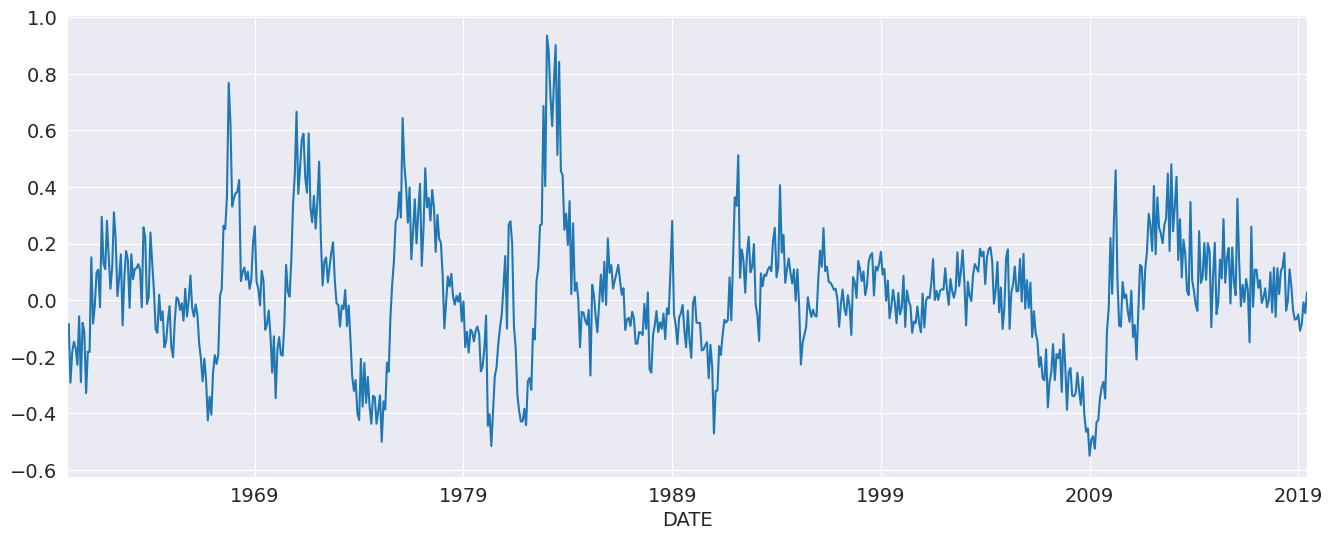
季节性动态¶

虽然 AutoReg 不直接支持季节性分量，因为它使用 OLS 估计参数，但可以通过使用过度参数化的季节性 AR 来捕获季节性动态，该季节性 AR 不对季节性 AR 中的限制进行约束。

[12]:

yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()
_, ax = plt.subplots()
ax = yoy_housing.plot(ax=ax)

../../../_images/examples_notebooks_generated_autoregressions_24_0.png

我们首先使用仅选择最大滞后的简单方法选择模型。所有较低的滞后都会自动包含。要检查的最大滞后设置为 13，因为这允许模型使用具有短期 AR(1) 分量和季节性 AR(1) 分量的季节性 AR，因此

\[(1-\phi_s L^{12})(1-\phi_1 L)y_t = \epsilon_t\]

展开后变为

\[y_t = \phi_1 y_{t-1} +\phi_s Y_{t-12} - \phi_1\phi_s Y_{t-13} + \epsilon_t\]

当展开时。 AutoReg 不强制执行结构，但可以估计嵌套模型

\[y_t = \phi_1 y_{t-1} +\phi_{12} Y_{t-12} - \phi_{13} Y_{t-13} + \epsilon_t.\]

我们看到所有 13 个滞后都被选中。

[13]:

sel = ar_select_order(yoy_housing, 13, old_names=False)
sel.ar_lags

[13]:

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]

所有 13 个滞后都是必需的似乎不太可能。我们可以设置 glob=True 以搜索所有 \(2^{13}\) 个包含最多 13 个滞后的模型。

在这里，我们看到选择了前三个滞后，第 7 个滞后也被选中，最后第 12 个和第 13 个滞后也被选中。这在表面上类似于上面描述的结构。

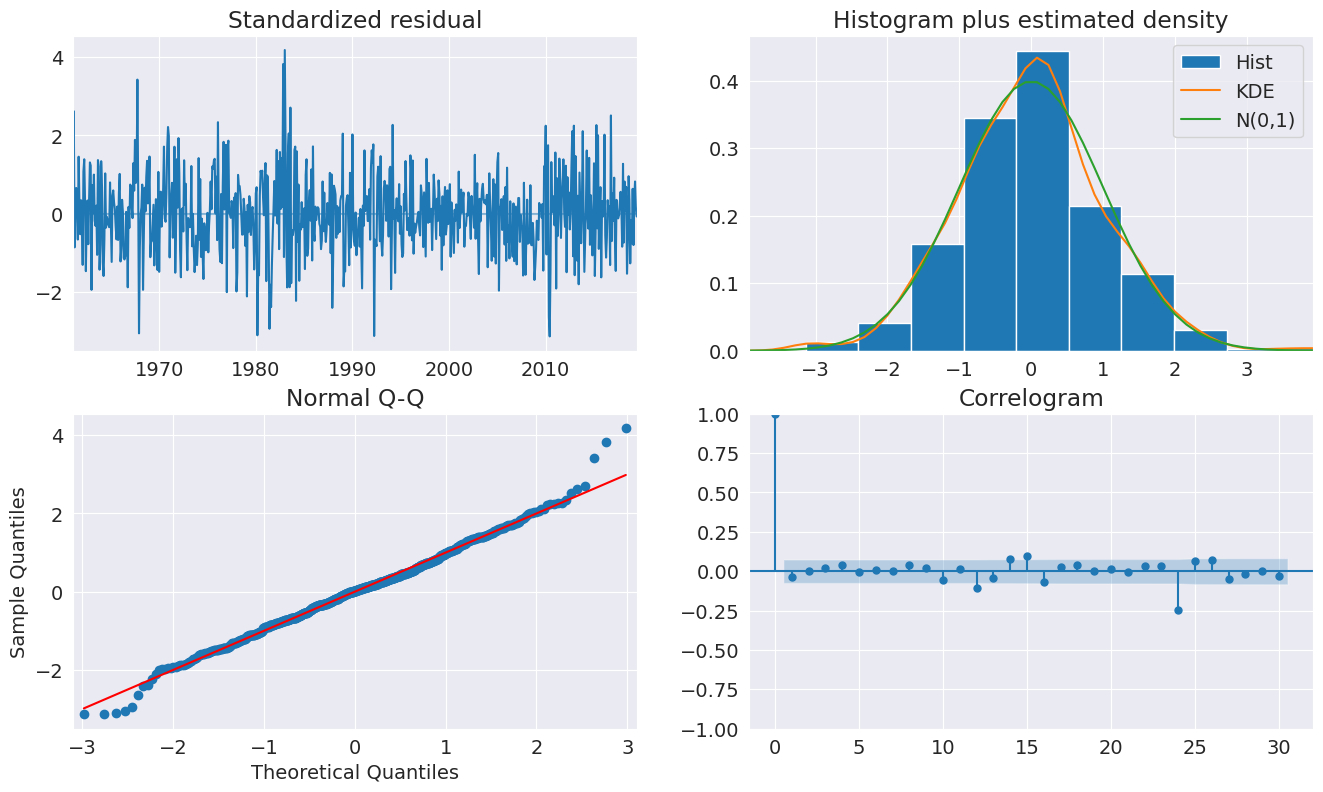
在拟合模型后，我们看一下诊断图，这些图表明该规范似乎足以捕获数据中的动态。

[14]:

sel = ar_select_order(yoy_housing, 13, glob=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  714
Model:             Restr. AutoReg(13)   Log Likelihood                 589.177
Method:               Conditional MLE   S.D. of innovations              0.104
Date:                Thu, 03 Oct 2024   AIC                          -1162.353
Time:                        15:55:45   BIC                          -1125.933
Sample:                    02-01-1961   HQIC                         -1148.276
                         - 06-01-2019
================================================================================
                   coef    std err          z      P>|z|      [0.025      0.975]
--------------------------------------------------------------------------------
const            0.0035      0.004      0.875      0.382      -0.004       0.011
HOUSTNSA.L1      0.5640      0.035     16.167      0.000       0.496       0.632
HOUSTNSA.L2      0.2347      0.038      6.238      0.000       0.161       0.308
HOUSTNSA.L3      0.2051      0.037      5.560      0.000       0.133       0.277
HOUSTNSA.L7     -0.0903      0.030     -2.976      0.003      -0.150      -0.031
HOUSTNSA.L12    -0.3791      0.034    -11.075      0.000      -0.446      -0.312
HOUSTNSA.L13     0.3354      0.033     10.254      0.000       0.271       0.400
                                    Roots
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -1.0309           -0.2682j            1.0652           -0.4595
AR.2            -1.0309           +0.2682j            1.0652            0.4595
AR.3            -0.7454           -0.7417j            1.0515           -0.3754
AR.4            -0.7454           +0.7417j            1.0515            0.3754
AR.5            -0.3172           -1.0221j            1.0702           -0.2979
AR.6            -0.3172           +1.0221j            1.0702            0.2979
AR.7             0.2419           -1.0573j            1.0846           -0.2142
AR.8             0.2419           +1.0573j            1.0846            0.2142
AR.9             0.7840           -0.8303j            1.1420           -0.1296
AR.10            0.7840           +0.8303j            1.1420            0.1296
AR.11            1.0730           -0.2386j            1.0992           -0.0348
AR.12            1.0730           +0.2386j            1.0992            0.0348
AR.13            1.1193           -0.0000j            1.1193           -0.0000
------------------------------------------------------------------------------

[15]:

fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)

../../../_images/examples_notebooks_generated_autoregressions_29_0.png

我们也可以包含季节性虚拟变量。由于模型使用的是同比变化，因此这些虚拟变量都是不显著的。

[16]:

sel = ar_select_order(yoy_housing, 13, glob=True, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

                               AutoReg Model Results
====================================================================================
Dep. Variable:                     HOUSTNSA   No. Observations:                  714
Model:             Restr. Seas. AutoReg(13)   Log Likelihood                 590.875
Method:                     Conditional MLE   S.D. of innovations              0.104
Date:                      Thu, 03 Oct 2024   AIC                          -1143.751
Time:                              16:08:11   BIC                          -1057.253
Sample:                          02-01-1961   HQIC                         -1110.317
                               - 06-01-2019
================================================================================
                   coef    std err          z      P>|z|      [0.025      0.975]
--------------------------------------------------------------------------------
const            0.0167      0.014      1.215      0.224      -0.010       0.044
s(2,12)         -0.0179      0.019     -0.931      0.352      -0.056       0.020
s(3,12)         -0.0121      0.019     -0.630      0.528      -0.050       0.026
s(4,12)         -0.0210      0.019     -1.089      0.276      -0.059       0.017
s(5,12)         -0.0223      0.019     -1.157      0.247      -0.060       0.015
s(6,12)         -0.0224      0.019     -1.160      0.246      -0.060       0.015
s(7,12)         -0.0212      0.019     -1.096      0.273      -0.059       0.017
s(8,12)         -0.0101      0.019     -0.520      0.603      -0.048       0.028
s(9,12)         -0.0095      0.019     -0.491      0.623      -0.047       0.028
s(10,12)        -0.0049      0.019     -0.252      0.801      -0.043       0.033
s(11,12)        -0.0084      0.019     -0.435      0.664      -0.046       0.030
s(12,12)        -0.0077      0.019     -0.400      0.689      -0.046       0.030
HOUSTNSA.L1      0.5630      0.035     16.160      0.000       0.495       0.631
HOUSTNSA.L2      0.2347      0.038      6.248      0.000       0.161       0.308
HOUSTNSA.L3      0.2075      0.037      5.634      0.000       0.135       0.280
HOUSTNSA.L7     -0.0916      0.030     -3.013      0.003      -0.151      -0.032
HOUSTNSA.L12    -0.3810      0.034    -11.149      0.000      -0.448      -0.314
HOUSTNSA.L13     0.3373      0.033     10.327      0.000       0.273       0.401
                                    Roots
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -1.0305           -0.2681j            1.0648           -0.4595
AR.2            -1.0305           +0.2681j            1.0648            0.4595
AR.3            -0.7447           -0.7414j            1.0509           -0.3754
AR.4            -0.7447           +0.7414j            1.0509            0.3754
AR.5            -0.3172           -1.0215j            1.0696           -0.2979
AR.6            -0.3172           +1.0215j            1.0696            0.2979
AR.7             0.2416           -1.0568j            1.0841           -0.2142
AR.8             0.2416           +1.0568j            1.0841            0.2142
AR.9             0.7837           -0.8304j            1.1418           -0.1296
AR.10            0.7837           +0.8304j            1.1418            0.1296
AR.11            1.0724           -0.2383j            1.0986           -0.0348
AR.12            1.0724           +0.2383j            1.0986            0.0348
AR.13            1.1192           -0.0000j            1.1192           -0.0000
------------------------------------------------------------------------------

工业生产¶

我们将使用工业生产指数数据来检查预测。

[17]:

data = pdr.get_data_fred("INDPRO", "1959-01-01", "2019-06-01")
ind_prod = data.INDPRO.pct_change(12).dropna().asfreq("MS")
_, ax = plt.subplots(figsize=(16, 9))
ind_prod.plot(ax=ax)

[17]:

<Axes: xlabel='DATE'>

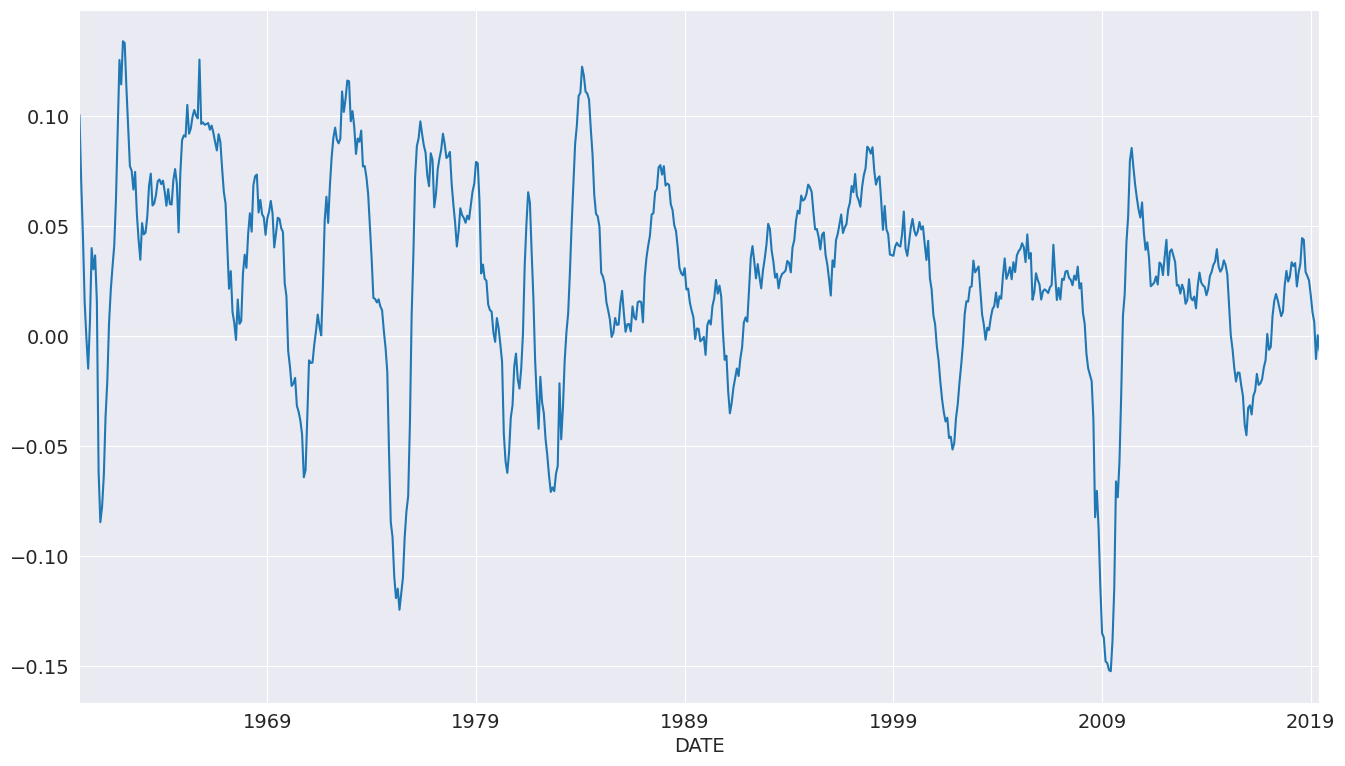
../../../_images/examples_notebooks_generated_autoregressions_33_1.png

我们将首先使用最多 12 个滞后来选择模型。即使许多系数不显著，AR(13) 仍然将 BIC 准则最小化。

[18]:

sel = ar_select_order(ind_prod, 13, "bic", old_names=False)
res = sel.model.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:                 INDPRO   No. Observations:                  714
Model:                    AutoReg(13)   Log Likelihood                2321.382
Method:               Conditional MLE   S.D. of innovations              0.009
Date:                Thu, 03 Oct 2024   AIC                          -4612.763
Time:                        16:08:12   BIC                          -4544.476
Sample:                    02-01-1961   HQIC                         -4586.368
                         - 06-01-2019
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0012      0.000      2.783      0.005       0.000       0.002
INDPRO.L1      1.1577      0.035     33.179      0.000       1.089       1.226
INDPRO.L2     -0.0822      0.053     -1.543      0.123      -0.187       0.022
INDPRO.L3   7.041e-05      0.053      0.001      0.999      -0.104       0.104
INDPRO.L4      0.0076      0.053      0.143      0.886      -0.096       0.111
INDPRO.L5     -0.1329      0.053     -2.529      0.011      -0.236      -0.030
INDPRO.L6     -0.0080      0.052     -0.153      0.879      -0.111       0.095
INDPRO.L7      0.0556      0.052      1.064      0.287      -0.047       0.158
INDPRO.L8     -0.0296      0.052     -0.568      0.570      -0.132       0.073
INDPRO.L9      0.0920      0.052      1.770      0.077      -0.010       0.194
INDPRO.L10    -0.0808      0.052     -1.552      0.121      -0.183       0.021
INDPRO.L11    -0.0003      0.052     -0.005      0.996      -0.102       0.102
INDPRO.L12    -0.3820      0.052     -7.364      0.000      -0.484      -0.280
INDPRO.L13     0.3613      0.033     10.996      0.000       0.297       0.426
                                    Roots
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -1.0408           -0.2913j            1.0808           -0.4566
AR.2            -1.0408           +0.2913j            1.0808            0.4566
AR.3            -0.7803           -0.8039j            1.1204           -0.3726
AR.4            -0.7803           +0.8039j            1.1204            0.3726
AR.5            -0.2728           -1.0533j            1.0880           -0.2903
AR.6            -0.2728           +1.0533j            1.0880            0.2903
AR.7             0.2716           -1.0507j            1.0852           -0.2097
AR.8             0.2716           +1.0507j            1.0852            0.2097
AR.9             0.8010           -0.7285j            1.0827           -0.1175
AR.10            0.8010           +0.7285j            1.0827            0.1175
AR.11            1.0219           -0.2219j            1.0457           -0.0340
AR.12            1.0219           +0.2219j            1.0457            0.0340
AR.13            1.0560           -0.0000j            1.0560           -0.0000
------------------------------------------------------------------------------

我们也可以使用全局搜索，允许在需要时加入更长的滞后，而无需要求加入更短的滞后。在这里，我们看到许多滞后被删除了。该模型表明数据中可能存在一些季节性。

[19]:

sel = ar_select_order(ind_prod, 13, "bic", glob=True, old_names=False)
sel.ar_lags
res_glob = sel.model.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:                 INDPRO   No. Observations:                  714
Model:                    AutoReg(13)   Log Likelihood                2321.382
Method:               Conditional MLE   S.D. of innovations              0.009
Date:                Thu, 03 Oct 2024   AIC                          -4612.763
Time:                        16:08:14   BIC                          -4544.476
Sample:                    02-01-1961   HQIC                         -4586.368
                         - 06-01-2019
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0012      0.000      2.783      0.005       0.000       0.002
INDPRO.L1      1.1577      0.035     33.179      0.000       1.089       1.226
INDPRO.L2     -0.0822      0.053     -1.543      0.123      -0.187       0.022
INDPRO.L3   7.041e-05      0.053      0.001      0.999      -0.104       0.104
INDPRO.L4      0.0076      0.053      0.143      0.886      -0.096       0.111
INDPRO.L5     -0.1329      0.053     -2.529      0.011      -0.236      -0.030
INDPRO.L6     -0.0080      0.052     -0.153      0.879      -0.111       0.095
INDPRO.L7      0.0556      0.052      1.064      0.287      -0.047       0.158
INDPRO.L8     -0.0296      0.052     -0.568      0.570      -0.132       0.073
INDPRO.L9      0.0920      0.052      1.770      0.077      -0.010       0.194
INDPRO.L10    -0.0808      0.052     -1.552      0.121      -0.183       0.021
INDPRO.L11    -0.0003      0.052     -0.005      0.996      -0.102       0.102
INDPRO.L12    -0.3820      0.052     -7.364      0.000      -0.484      -0.280
INDPRO.L13     0.3613      0.033     10.996      0.000       0.297       0.426
                                    Roots
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -1.0408           -0.2913j            1.0808           -0.4566
AR.2            -1.0408           +0.2913j            1.0808            0.4566
AR.3            -0.7803           -0.8039j            1.1204           -0.3726
AR.4            -0.7803           +0.8039j            1.1204            0.3726
AR.5            -0.2728           -1.0533j            1.0880           -0.2903
AR.6            -0.2728           +1.0533j            1.0880            0.2903
AR.7             0.2716           -1.0507j            1.0852           -0.2097
AR.8             0.2716           +1.0507j            1.0852            0.2097
AR.9             0.8010           -0.7285j            1.0827           -0.1175
AR.10            0.8010           +0.7285j            1.0827            0.1175
AR.11            1.0219           -0.2219j            1.0457           -0.0340
AR.12            1.0219           +0.2219j            1.0457            0.0340
AR.13            1.0560           -0.0000j            1.0560           -0.0000
------------------------------------------------------------------------------

plot_predict 可用于生成预测图以及置信区间。在这里，我们从最后一个观测值开始生成预测，并持续 18 个月。

[20]:

ind_prod.shape

[20]:

(714,)

[21]:

fig = res_glob.plot_predict(start=714, end=732)

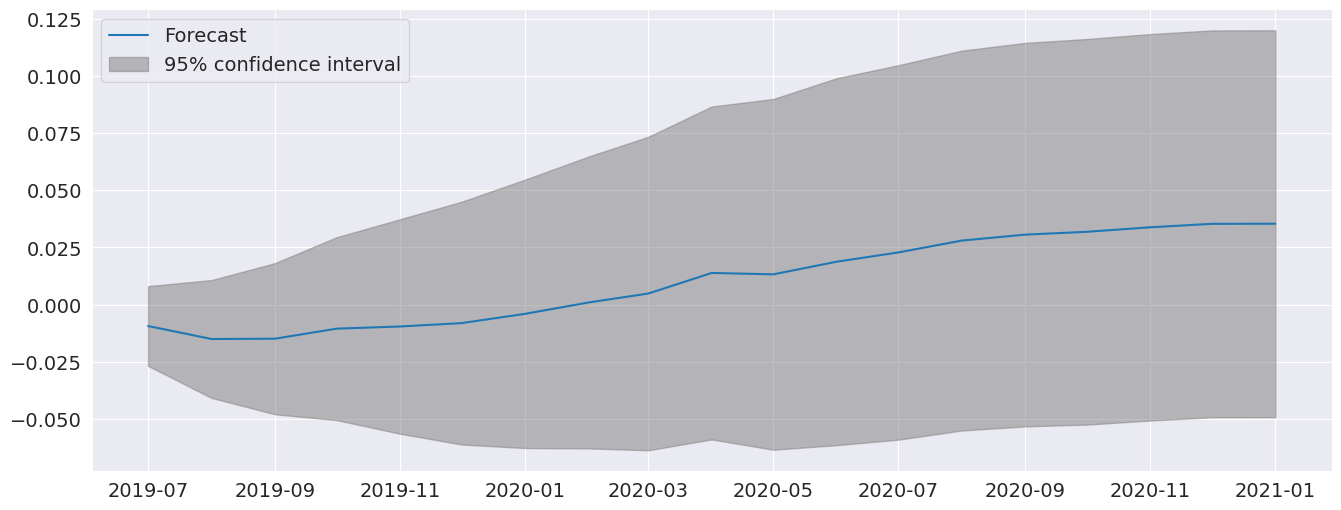
../../../_images/examples_notebooks_generated_autoregressions_40_0.png

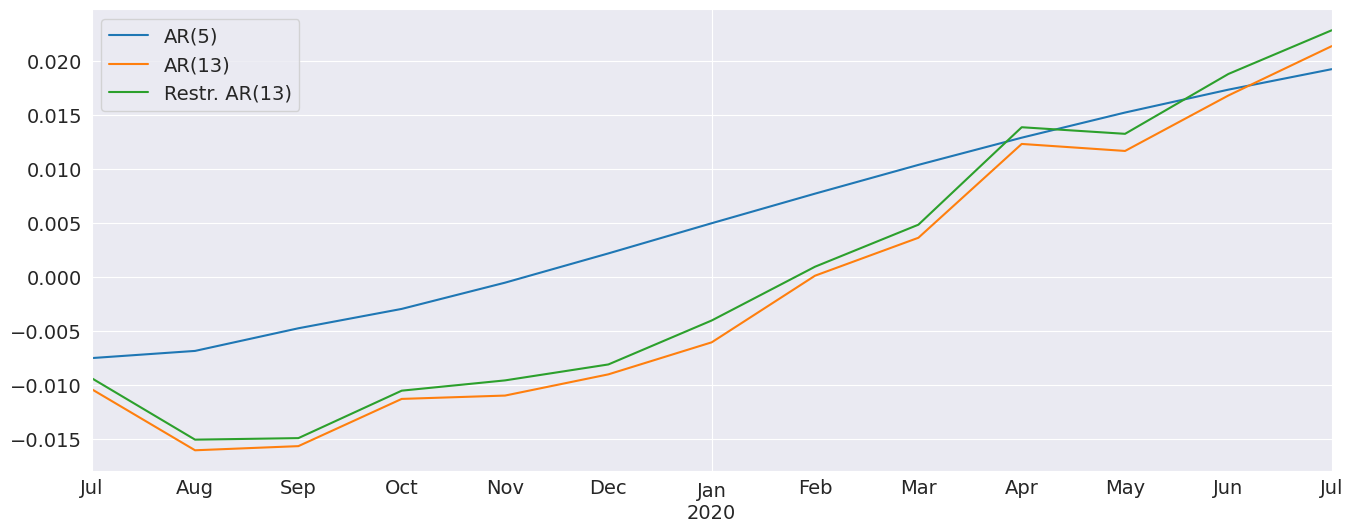
完整模型和受限模型的预测非常相似。我还包括一个 AR(5)，它具有非常不同的动态。

[22]:

res_ar5 = AutoReg(ind_prod, 5, old_names=False).fit()
predictions = pd.DataFrame(
    {
        "AR(5)": res_ar5.predict(start=714, end=726),
        "AR(13)": res.predict(start=714, end=726),
        "Restr. AR(13)": res_glob.predict(start=714, end=726),
    }
)
_, ax = plt.subplots()
ax = predictions.plot(ax=ax)

../../../_images/examples_notebooks_generated_autoregressions_42_0.png

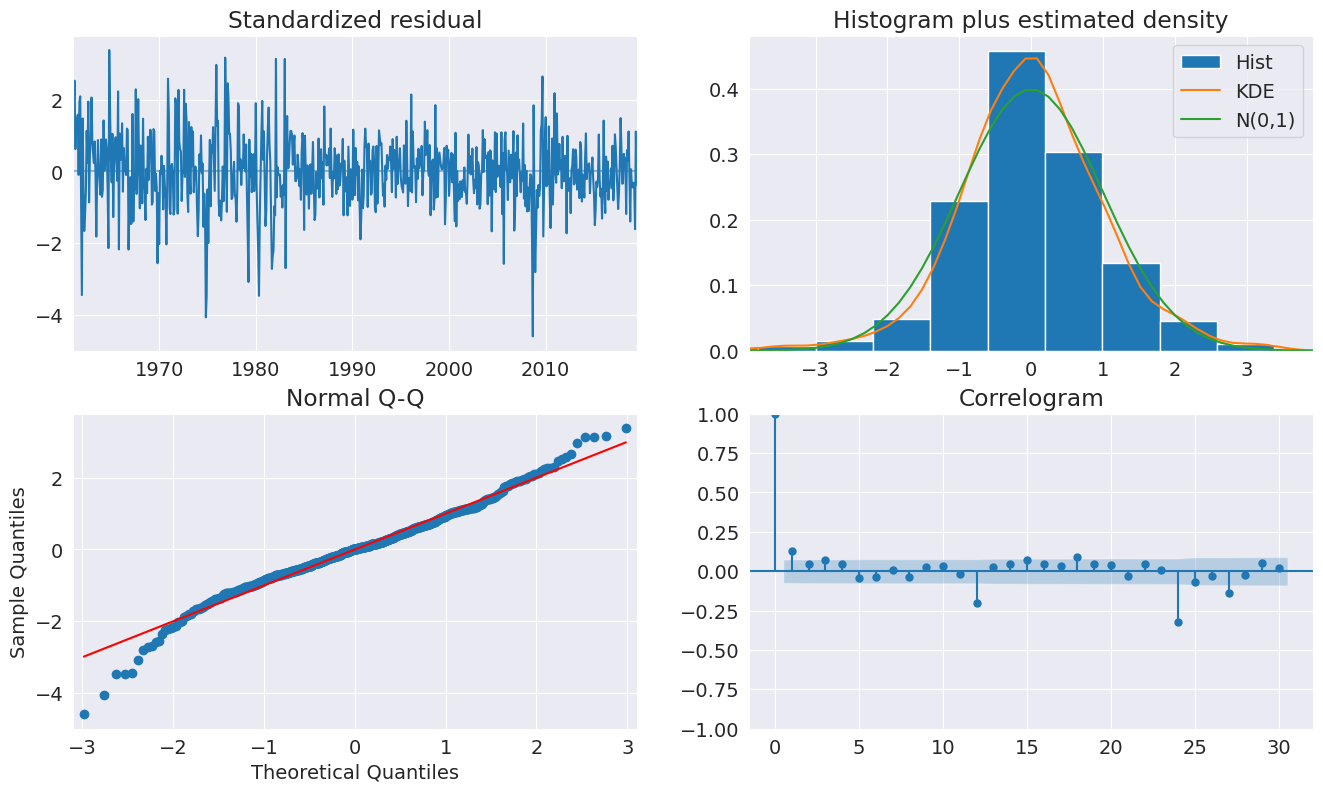
诊断结果表明该模型捕获了数据中的大部分动态。ACF 在季节性频率上显示出一种模式，因此可能需要更完整的季节性模型 (SARIMAX)。

[23]:

fig = plt.figure(figsize=(16, 9))
fig = res_glob.plot_diagnostics(fig=fig, lags=30)

../../../_images/examples_notebooks_generated_autoregressions_44_0.png

预测¶

使用结果实例中的 predict 方法生成预测。默认情况下会生成静态预测，即一步预测。生成多步预测需要使用 dynamic=True。

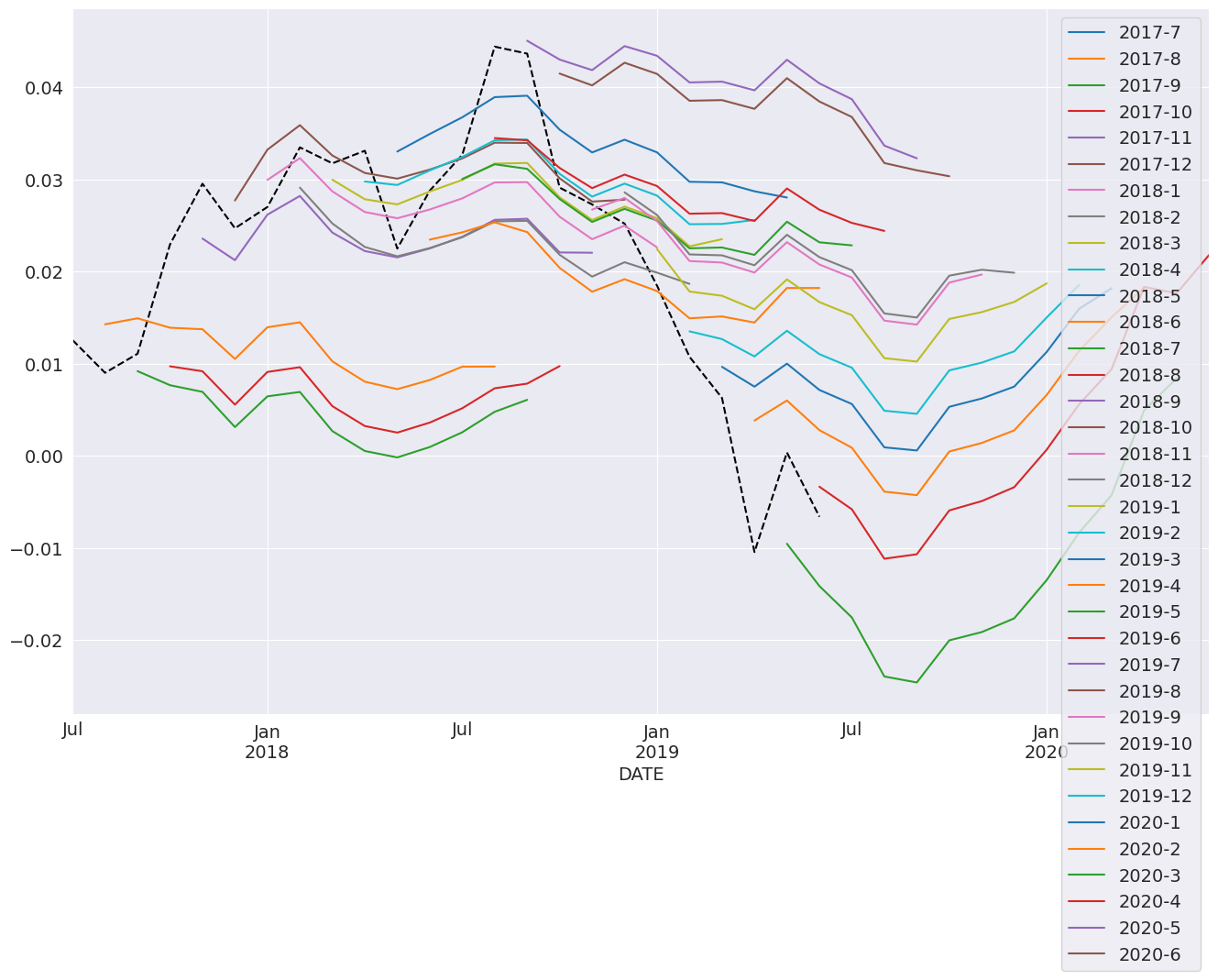
在下一个单元格中，我们为样本中的最后 24 个周期生成 12 步超前预测。这需要一个循环。

**注意**：这些预测在技术上是样本内的，因为用于预测的数据用于估计参数。生成 OOS 预测需要两个模型。第一个模型必须排除 OOS 期间。第二个模型使用来自完整样本模型的 predict 方法，并使用来自排除 OOS 期间的较短样本模型的参数。

[24]:

import numpy as np

start = ind_prod.index[-24]
forecast_index = pd.date_range(start, freq=ind_prod.index.freq, periods=36)
cols = ["-".join(str(val) for val in (idx.year, idx.month)) for idx in forecast_index]
forecasts = pd.DataFrame(index=forecast_index, columns=cols)
for i in range(1, 24):
    fcast = res_glob.predict(
        start=forecast_index[i], end=forecast_index[i + 12], dynamic=True
    )
    forecasts.loc[fcast.index, cols[i]] = fcast
_, ax = plt.subplots(figsize=(16, 10))
ind_prod.iloc[-24:].plot(ax=ax, color="black", linestyle="--")
ax = forecasts.plot(ax=ax)

../../../_images/examples_notebooks_generated_autoregressions_46_0.png

与 SARIMAX 比较¶

SARIMAX 是具有外生回归量的季节性自回归积分移动平均模型的实现。它支持

季节性和非季节性 AR 和 MA 分量的规范
包含外生变量
使用卡尔曼滤波器进行完全最大似然估计

此模型比 AutoReg 功能更丰富。与 SARIMAX 不同，AutoReg 使用 OLS 估计参数。这更快，问题是全局凸的，因此不存在局部最小值问题。闭式估计器及其性能是 AutoReg 与 SARIMAX 比较 AR(P) 模型时的主要优势。 AutoReg 还支持季节性虚拟变量，如果用户将它们作为外生回归量包含在内，则可以在 SARIMAX 中使用这些虚拟变量。

[25]:

from statsmodels.tsa.api import SARIMAX

sarimax_mod = SARIMAX(ind_prod, order=((1, 5, 12, 13), 0, 0), trend="c")
sarimax_res = sarimax_mod.fit()
print(sarimax_res.summary())

RUNNING THE L-BFGS-B CODE

           * * *

Machine precision = 2.220D-16
 N =            6     M =           10

At X0         0 variables are exactly at the bounds

At iterate    0    f= -3.21907D+00    |proj g|=  1.78480D+01

 This problem is unconstrained.

At iterate    5    f= -3.22490D+00    |proj g|=  1.52242D-01

At iterate   10    f= -3.22526D+00    |proj g|=  1.46006D+00

At iterate   15    f= -3.22550D+00    |proj g|=  7.46711D-01

At iterate   20    f= -3.22610D+00    |proj g|=  2.52890D-01

At iterate   25    f= -3.22611D+00    |proj g|=  1.80088D-01

At iterate   30    f= -3.22646D+00    |proj g|=  1.46895D+00

At iterate   35    f= -3.22677D+00    |proj g|=  1.05336D-01

At iterate   40    f= -3.22678D+00    |proj g|=  3.20093D-02

           * * *

Tit   = total number of iterations
Tnf   = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip  = number of BFGS updates skipped
Nact  = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F     = final function value

           * * *

   N    Tit     Tnf  Tnint  Skip  Nact     Projg        F
    6     41     64      1     0     0   3.201D-02  -3.227D+00
  F =  -3.2267786140514940

CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
                                     SARIMAX Results
=========================================================================================
Dep. Variable:                            INDPRO   No. Observations:                  714
Model:             SARIMAX([1, 5, 12, 13], 0, 0)   Log Likelihood                2303.920
Date:                           Thu, 03 Oct 2024   AIC                          -4595.840
Time:                                   16:08:18   BIC                          -4568.415
Sample:                               01-01-1960   HQIC                         -4585.248
                                    - 06-01-2019
Covariance Type:                             opg
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.0011      0.000      2.534      0.011       0.000       0.002
ar.L1          1.0801      0.010    107.331      0.000       1.060       1.100
ar.L5         -0.0847      0.011     -7.592      0.000      -0.107      -0.063
ar.L12        -0.4428      0.026    -17.302      0.000      -0.493      -0.393
ar.L13         0.4073      0.025     16.213      0.000       0.358       0.457
sigma2      9.136e-05   3.08e-06     29.630      0.000    8.53e-05    9.74e-05
===================================================================================
Ljung-Box (L1) (Q):                  21.77   Jarque-Bera (JB):               959.65
Prob(Q):                              0.00   Prob(JB):                         0.00
Heteroskedasticity (H):               0.37   Skew:                            -0.63
Prob(H) (two-sided):                  0.00   Kurtosis:                         8.54
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

 Warning:  more than 10 function and gradient
   evaluations in the last line search.  Termination
   may possibly be caused by a bad search direction.

[26]:

sarimax_params = sarimax_res.params.iloc[:-1].copy()
sarimax_params.index = res_glob.params.index
params = pd.concat([res_glob.params, sarimax_params], axis=1, sort=False)
params.columns = ["AutoReg", "SARIMAX"]
params

[26]:

	AutoReg	SARIMAX
const	0.001234	0.001085
INDPRO.L1	1.088761	1.080116
INDPRO.L5	-0.105665	-0.084738
INDPRO.L12	-0.388374	-0.442793
INDPRO.L13	0.362319	0.407338

自定义确定性过程¶

deterministic 参数允许使用自定义 DeterministicProcess。这允许构建更复杂的确定性项，例如包含两个周期的季节性分量，或者，如下一个示例所示，使用傅里叶级数而不是季节性虚拟变量。

[27]:

from statsmodels.tsa.deterministic import DeterministicProcess

dp = DeterministicProcess(housing.index, constant=True, period=12, fourier=2)
mod = AutoReg(housing, 2, trend="n", seasonal=False, deterministic=dp)
res = mod.fit()
print(res.summary())

                            AutoReg Model Results
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  725
Model:                     AutoReg(2)   Log Likelihood               -2716.505
Method:               Conditional MLE   S.D. of innovations             10.364
Date:                Thu, 03 Oct 2024   AIC                           5449.010
Time:                        16:08:18   BIC                           5485.677
Sample:                    04-01-1959   HQIC                          5463.163
                         - 06-01-2019
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
const           1.7550      0.391      4.485      0.000       0.988       2.522
sin(1,12)      16.7443      0.860     19.478      0.000      15.059      18.429
cos(1,12)       4.9409      0.588      8.409      0.000       3.789       6.093
sin(2,12)      12.9364      0.619     20.889      0.000      11.723      14.150
cos(2,12)      -0.4738      0.754     -0.628      0.530      -1.952       1.004
HOUSTNSA.L1    -0.3905      0.037    -10.664      0.000      -0.462      -0.319
HOUSTNSA.L2    -0.1746      0.037     -4.769      0.000      -0.246      -0.103
                                    Roots
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1           -1.1182           -2.1159j            2.3932           -0.3274
AR.2           -1.1182           +2.1159j            2.3932            0.3274
-----------------------------------------------------------------------------

[28]:

fig = res.plot_predict(720, 840)

../../../_images/examples_notebooks_generated_autoregressions_52_0.png

上次更新：2024 年 10 月 3 日