障碍计数模型和截断计数模型¶
作者:Josef Perktold
Statsmodels 现在添加了障碍计数模型和截断计数模型,从 0.14 版本开始。
障碍模型由一个用于零计数的模型和一个用于大于零计数的分布模型组成。零模型是针对零计数与大于零计数的二元模型。用于非零计数的计数模型是零截断计数模型。
Statsmodels 目前支持使用泊松分布和负二项分布作为零模型和计数模型的障碍模型。Logit、Probit 或 GLM-Binomial 等二元模型尚未支持作为零模型。泊松-泊松障碍模型的优势在于,标准泊松模型是两个模型参数相等的特例。这为障碍模型相对于泊松模型提供了简单的 Wald 检验。
实现的二元模型是一个被截断模型,其中观测值在 1 处被右截断。这意味着只观察到 0 或 1 的计数。
障碍模型可以通过分别估计零模型和针对零截断数据的计数模型来估计,假设观测值独立分布(观测值之间没有相关性)。得到的参数估计协方差矩阵是对角块矩阵,对角块由子模型给出。联合估计尚未实现。
被截断和截断计数模型主要为了支持障碍模型而开发。然而,左截断计数模型在除支持障碍模型之外的其他应用中也有用。右截断模型没有单独的意义,因为它们只支持可以通过 GLM-Binomial、Logit 或 Probit 建模的二元观测值。
对于障碍模型,只有一个类 HurdleCountModel,其中包含子模型的分布作为选项。目前用于截断模型的类有 TruncatedLFPoisson 和 TruncatedLFNegativeBinomialP,其中“LF”代表在固定且与观测值无关的截断点处的左截断。
[ ]:
[1]:
import numpy as np
import pandas as pd
import statsmodels.discrete.truncated_model as smtc
from statsmodels.discrete.discrete_model import (
Poisson, NegativeBinomial, NegativeBinomialP, GeneralizedPoisson)
from statsmodels.discrete.count_model import (
ZeroInflatedPoisson,
ZeroInflatedGeneralizedPoisson,
ZeroInflatedNegativeBinomialP
)
from statsmodels.discrete.truncated_model import (
TruncatedLFPoisson,
TruncatedLFNegativeBinomialP,
_RCensoredPoisson,
HurdleCountModel,
)
模拟障碍模型¶
我们明确模拟泊松-泊松障碍模型,因为目前还没有针对它的分布辅助函数。
[2]:
np.random.seed(987456348)
# large sample to get strong results
nobs = 5000
x = np.column_stack((np.ones(nobs), np.linspace(0, 1, nobs)))
mu0 = np.exp(0.5 *2 * x.sum(1))
y = np.random.poisson(mu0, size=nobs)
print(np.bincount(y))
y_ = y
indices = np.arange(len(y))
mask = mask0 = y > 0
for _ in range(10):
print( mask.sum())
indices = mask #indices[mask]
if not np.any(mask):
break
mu_ = np.exp(0.5 * x[indices].sum(1))
y[indices] = y_ = np.random.poisson(mu_, size=len(mu_))
np.place(y, mask, y_)
mask = np.logical_and(mask0, y == 0)
np.bincount(y)
[102 335 590 770 816 739 573 402 265 176 116 59 35 7 11 4]
4898
602
93
11
2
0
[2]:
array([ 102, 1448, 1502, 1049, 542, 234, 81, 31, 6, 5])
估计错误指定的泊松模型¶
我们生成的数据存在零计数不足,即我们观察到的零计数少于泊松模型中预期的零计数。
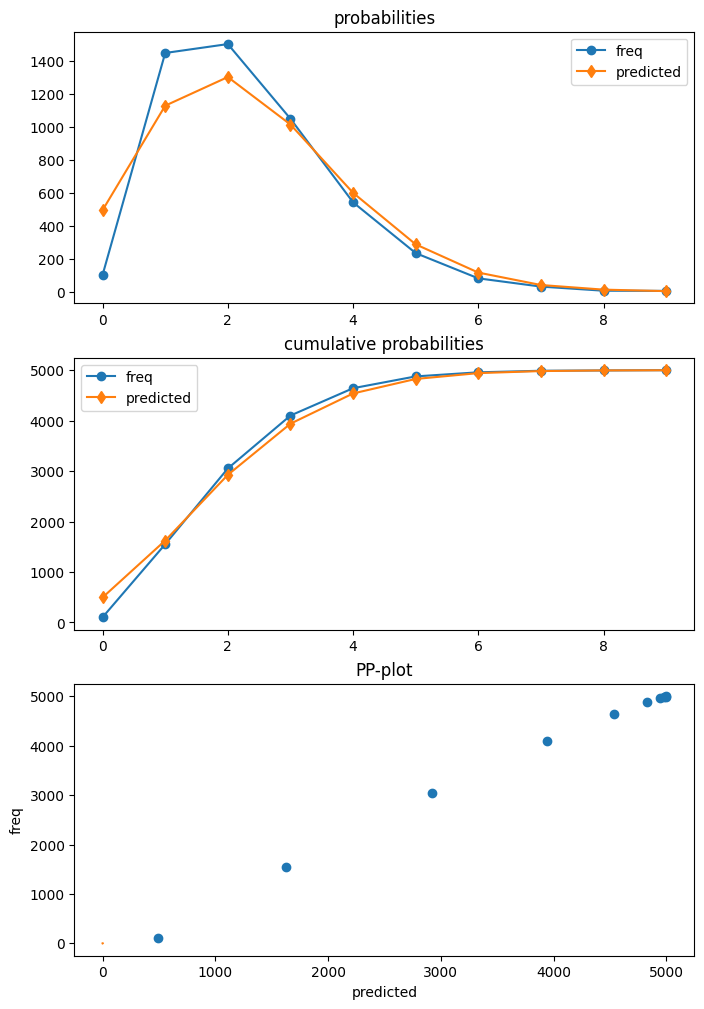
拟合模型后,我们可以使用泊松诊断类中的绘图函数来比较预期预测分布和实际频率。这表明泊松模型高估了零计数,低估了一和二的计数。
[3]:
mod_p = Poisson(y, x)
res_p = mod_p.fit()
print(res_p.summary())
Optimization terminated successfully.
Current function value: 1.668079
Iterations 4
Poisson Regression Results
==============================================================================
Dep. Variable: y No. Observations: 5000
Model: Poisson Df Residuals: 4998
Method: MLE Df Model: 1
Date: Thu, 03 Oct 2024 Pseudo R-squ.: 0.008678
Time: 15:44:58 Log-Likelihood: -8340.4
converged: True LL-Null: -8413.4
Covariance Type: nonrobust LLR p-value: 1.279e-33
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.6532 0.019 33.642 0.000 0.615 0.691
x1 0.3871 0.032 12.062 0.000 0.324 0.450
==============================================================================
[4]:
dia_p = res_p.get_diagnostic()
dia_p.plot_probs();
估计障碍模型¶
接下来,我们估计正确指定的泊松-泊松障碍模型。
HurdleCountModel 的签名和选项表明泊松-泊松是默认值,因此在创建此模型时无需指定任何选项。
HurdleCountModel(endog, exog, offset=None, dist='poisson', zerodist='poisson', p=2, pzero=2, exposure=None, missing='none', **kwargs)
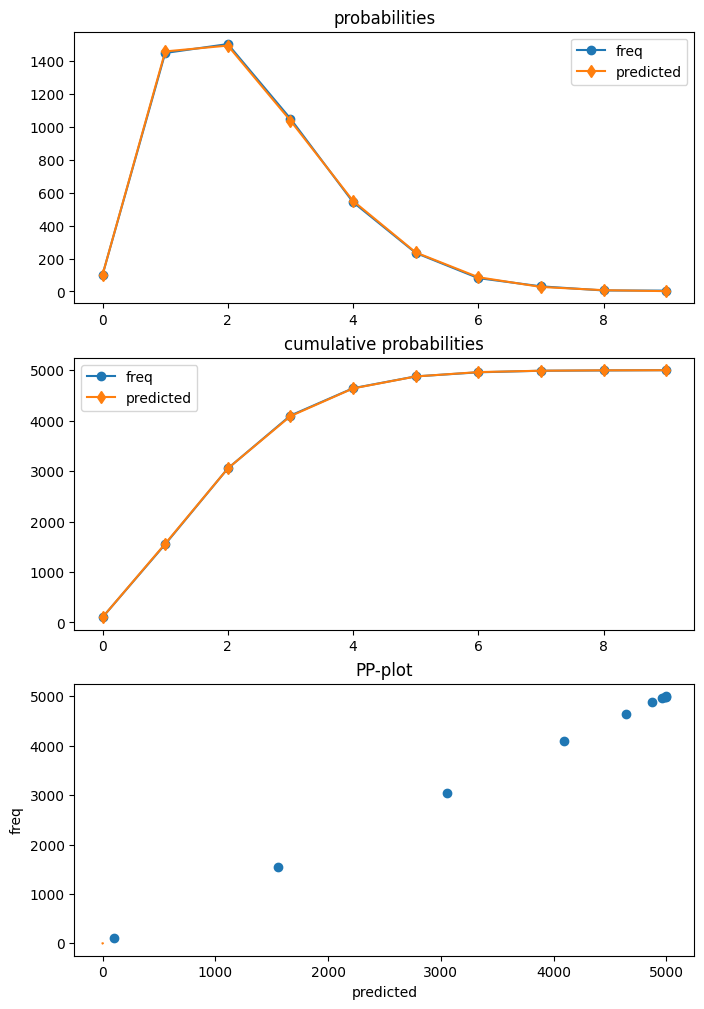
HurdleCountModel 的结果类具有一个 get_diagnostic 方法。但是,目前仅提供部分诊断方法。预测分布的绘图显示与数据高度一致。
[5]:
mod_h = HurdleCountModel(y, x)
res_h = mod_h.fit(disp=False)
print(res_h.summary())
HurdleCountModel Regression Results
==============================================================================
Dep. Variable: y No. Observations: 5000
Model: HurdleCountModel Df Residuals: 4996
Method: MLE Df Model: 2
Date: Thu, 03 Oct 2024 Pseudo R-squ.: 0.01503
Time: 15:44:59 Log-Likelihood: -8004.9
converged: [True, True] LL-Null: -8127.1
Covariance Type: nonrobust LLR p-value: 8.901e-54
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
zm_const 0.9577 0.048 20.063 0.000 0.864 1.051
zm_x1 1.0576 0.121 8.737 0.000 0.820 1.295
const 0.5009 0.024 20.875 0.000 0.454 0.548
x1 0.4577 0.039 11.882 0.000 0.382 0.533
==============================================================================
[6]:
dia_h = res_h.get_diagnostic()
dia_h.plot_probs();
我们可以使用 Wald 检验来检验零模型的参数是否与零截断计数模型的参数相同。p 值非常小,并且正确拒绝了模型只是泊松模型的假设。我们使用的是大型样本量,因此在这种情况下,检验的功效将会很大。
[7]:
res_h.wald_test("zm_const = const, zm_x1 = x1", scalar=True)
[7]:
<class 'statsmodels.stats.contrast.ContrastResults'>
<Wald test (chi2): statistic=470.67320754391915, p-value=6.231772522807044e-103, df_denom=2>
预测¶
障碍模型可用于预测整体模型和两个子模型的统计量。要预测的统计量使用 which 关键字指定。
以下内容取自 predict 的文档字符串,列出了可用的选项。
which : str (optional)
Statitistic to predict. Default is 'mean'.
- 'mean' : the conditional expectation of endog E(y | x)
- 'mean-main' : mean parameter of truncated count model.
Note, this is not the mean of the truncated distribution.
- 'linear' : the linear predictor of the truncated count model.
- 'var' : returns the estimated variance of endog implied by the
model.
- 'prob-main' : probability of selecting the main model which is
the probability of observing a nonzero count P(y > 0 | x).
- 'prob-zero' : probability of observing a zero count. P(y=0 | x).
This is equal to is ``1 - prob-main``
- 'prob-trunc' : probability of truncation of the truncated count
model. This is the probability of observing a zero count implied
by the truncation model.
- 'mean-nonzero' : expected value conditional on having observation
larger than zero, E(y | X, y>0)
- 'prob' : probabilities of each count from 0 to max(endog), or
for y_values if those are provided. This is a multivariate
return (2-dim when predicting for several observations).
这些选项在结果类的 predict 和 get_prediction 方法中可用。
对于以下示例,我们创建了一组解释变量,这些变量是从原始数据中以等间距间隔取出的。然后我们可以根据这些解释变量预测可用的统计量。
[8]:
which_options = ["mean", "mean-main", "linear", "mean-nonzero", "prob-zero", "prob-main", "prob-trunc", "var", "prob"]
ex = x[slice(None, None, nobs // 5), :]
ex
[8]:
array([[1. , 0. ],
[1. , 0.20004001],
[1. , 0.40008002],
[1. , 0.60012002],
[1. , 0.80016003]])
[9]:
for w in which_options:
print(w)
pred = res_h.predict(ex, which=w)
print(" ", pred)
mean
[1.89150663 2.07648059 2.25555158 2.43319456 2.61673457]
mean-main
[1.65015181 1.8083782 1.98177629 2.17180081 2.38004602]
linear
[0.50086729 0.59243042 0.68399356 0.77555669 0.86711982]
mean-nonzero
[2.04231955 2.16292424 2.29857565 2.45116551 2.62277411]
prob-zero
[0.07384394 0.0399661 0.01871771 0.00733159 0.00230273]
prob-main
[0.92615606 0.9600339 0.98128229 0.99266841 0.99769727]
prob-trunc
[0.19202076 0.16391977 0.1378242 0.11397219 0.09254632]
var
[1.43498239 1.51977118 1.63803729 1.7971727 1.99738345]
prob
[[7.38439416e-02 3.63208532e-01 2.99674608e-01 1.64836199e-01
6.80011882e-02 2.24424568e-02 6.17224344e-03 1.45501981e-03
3.00125448e-04 5.50280612e-05]
[3.99660987e-02 3.40376213e-01 3.07764462e-01 1.85518182e-01
8.38717591e-02 3.03343722e-02 9.14266959e-03 2.36191491e-03
5.33904431e-04 1.07277904e-04]
[1.87177088e-02 3.10869602e-01 3.08037002e-01 2.03486809e-01
1.00816333e-01 3.99590837e-02 1.31983274e-02 3.73659033e-03
9.25635762e-04 2.03822556e-04]
[7.33159258e-03 2.77316512e-01 3.01138113e-01 2.18003999e-01
1.18365316e-01 5.14131777e-02 1.86098635e-02 5.77384524e-03
1.56745522e-03 3.78244503e-04]
[2.30272798e-03 2.42169151e-01 2.88186862e-01 2.28632665e-01
1.36039066e-01 6.47558475e-02 2.56869828e-02 8.73374304e-03
2.59833880e-03 6.87129546e-04]]
[10]:
for w in which_options[:-1]:
print(w)
pred = res_h.get_prediction(ex, which=w)
print(" ", pred.predicted)
print(" se", pred.se)
mean
[1.89150663 2.07648059 2.25555158 2.43319456 2.61673457]
se [0.07877461 0.05693768 0.05866892 0.09551274 0.15359057]
mean-main
[1.65015181 1.8083782 1.98177629 2.17180081 2.38004602]
se [0.03959242 0.03164634 0.02471869 0.02415162 0.03453261]
linear
[0.50086729 0.59243042 0.68399356 0.77555669 0.86711982]
se [0.04773779 0.03148549 0.02960421 0.04397859 0.06453261]
mean-nonzero
[2.04231955 2.16292424 2.29857565 2.45116551 2.62277411]
se [0.02978486 0.02443098 0.01958745 0.0196433 0.02881753]
prob-zero
[0.07384394 0.0399661 0.01871771 0.00733159 0.00230273]
se [0.00918583 0.00405155 0.00220446 0.00158494 0.00090255]
prob-main
[0.92615606 0.9600339 0.98128229 0.99266841 0.99769727]
se [0.00918583 0.00405155 0.00220446 0.00158494 0.00090255]
prob-trunc
[0.19202076 0.16391977 0.1378242 0.11397219 0.09254632]
se [0.00760257 0.00518746 0.00340683 0.00275261 0.00319587]
var
[1.43498239 1.51977118 1.63803729 1.7971727 1.99738345]
se [0.04853902 0.03615054 0.02747485 0.02655145 0.03733328]
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/base/_prediction_inference.py:782: UserWarning: using default log-link in get_prediction
warnings.warn("using default log-link in get_prediction")
选项 which="prob" 返回预测 exog 预测数组的每一行的预测概率。我们通常对所有 exog 的平均概率感兴趣。预测方法有一个选项 average=True 用于计算预测值的跨观测值的平均值以及这些平均预测值的对应标准误差和置信区间。
[11]:
pred = res_h.get_prediction(ex, which="prob", average=True)
print(" ", pred.predicted)
print(" se", pred.se)
[2.84324139e-02 3.06788002e-01 3.00960210e-01 2.00095571e-01
1.01418732e-01 4.17809876e-02 1.45620174e-02 4.41222267e-03
1.18509193e-03 2.86300514e-04]
se [2.81472152e-03 5.00830805e-03 1.37524763e-03 1.87343644e-03
1.99068649e-03 1.23878525e-03 5.78099173e-04 2.21180110e-04
7.25021189e-05 2.08872558e-05]
我们使用 panda DataFrame 来获得更易于阅读的显示。 “predicted” 列显示了根据 exog 的 5 个网格点平均的预测响应值分布的概率质量函数。这些概率加起来不等于 1,因为比观测到的计数更大的计数具有正概率,并且在表中缺失,尽管在这个示例中,该概率很小。
[12]:
dfp_h = pred.summary_frame()
dfp_h
[12]:
| predicted | se | ci_lower | ci_upper | |
|---|---|---|---|---|
| 0 | 0.028432 | 0.002815 | 0.022916 | 0.033949 |
| 1 | 0.306788 | 0.005008 | 0.296972 | 0.316604 |
| 2 | 0.300960 | 0.001375 | 0.298265 | 0.303656 |
| 3 | 0.200096 | 0.001873 | 0.196424 | 0.203767 |
| 4 | 0.101419 | 0.001991 | 0.097517 | 0.105320 |
| 5 | 0.041781 | 0.001239 | 0.039353 | 0.044209 |
| 6 | 0.014562 | 0.000578 | 0.013429 | 0.015695 |
| 7 | 0.004412 | 0.000221 | 0.003979 | 0.004846 |
| 8 | 0.001185 | 0.000073 | 0.001043 | 0.001327 |
| 9 | 0.000286 | 0.000021 | 0.000245 | 0.000327 |
[13]:
prob_larger9 = pred.predicted.sum()
prob_larger9, 1 - prob_larger9
[13]:
(np.float64(0.9999215487936677), np.float64(7.84512063323195e-05))
get_prediction 在这种情况下返回一个基本 PredictionResultsDelta 类实例。
使用 delta 方法计算依赖于多个分布参数的非线性函数的标准误差、p 值和置信区间等推断统计量。预测的推断基于正态分布。
[14]:
pred
[14]:
<statsmodels.base._prediction_inference.PredictionResultsDelta at 0x7f68ba217ee0>
[15]:
pred.dist, pred.dist_args
[15]:
(<scipy.stats._continuous_distns.norm_gen at 0x7f68c0dc2a40>, ())
我们可以将障碍模型预测的分布与之前估计的泊松模型预测的分布进行比较。最后一列“diff”显示泊松模型高估了零计数约 8% 的观测值,并且低估了一和二的计数约 7% 和 3.7%,分别在 exog 网格的平均值上。
[16]:
pred_p = res_p.get_prediction(ex, which="prob", average=True)
dfp_p = pred_p.summary_frame()
dfp_h["poisson"] = dfp_p["predicted"]
dfp_h["diff"] = dfp_h["poisson"] - dfp_h["predicted"]
dfp_h
[16]:
| predicted | se | ci_lower | ci_upper | poisson | diff | |
|---|---|---|---|---|---|---|
| 0 | 0.028432 | 0.002815 | 0.022916 | 0.033949 | 0.107848 | 0.079416 |
| 1 | 0.306788 | 0.005008 | 0.296972 | 0.316604 | 0.237020 | -0.069768 |
| 2 | 0.300960 | 0.001375 | 0.298265 | 0.303656 | 0.263523 | -0.037437 |
| 3 | 0.200096 | 0.001873 | 0.196424 | 0.203767 | 0.197657 | -0.002439 |
| 4 | 0.101419 | 0.001991 | 0.097517 | 0.105320 | 0.112511 | 0.011093 |
| 5 | 0.041781 | 0.001239 | 0.039353 | 0.044209 | 0.051833 | 0.010052 |
| 6 | 0.014562 | 0.000578 | 0.013429 | 0.015695 | 0.020124 | 0.005561 |
| 7 | 0.004412 | 0.000221 | 0.003979 | 0.004846 | 0.006769 | 0.002356 |
| 8 | 0.001185 | 0.000073 | 0.001043 | 0.001327 | 0.002012 | 0.000827 |
| 9 | 0.000286 | 0.000021 | 0.000245 | 0.000327 | 0.000537 | 0.000250 |
其他估计后操作¶
估计的障碍模型可用于进行参数的 Wald 检验和预测。其他最大似然统计量,如对数似然值和信息准则,也可获得。
但是,某些需要估计、参数推断和预测不需要的辅助函数的估计后方法目前尚不可用。主要不支持的方法是 score_test、get_distribution 和 get_influence。 get_diagnostics 中的诊断措施仅适用于基于预测的统计量。
[17]:
res_h.llf, res_h.df_resid, res_h.aic, res_h.bic
[17]:
(np.float64(-8004.904002793644),
4996,
np.float64(16017.808005587289),
np.float64(16043.876778352953))
是否存在过度离散?我们可以使用皮尔逊残差来计算皮尔逊卡方统计量,如果模型指定正确,该统计量应该接近 1。
[18]:
(res_h.resid_pearson**2).sum() / res_h.df_resid
[18]:
np.float64(0.9989670114949286)
诊断类还具有预测分布,用于诊断图。目前没有其他统计量或检验可用。
[19]:
dia_h.probs_predicted.mean(0)
[19]:
array([0.02044612, 0.29147174, 0.29856288, 0.20740118, 0.10990976,
0.04737579, 0.0172898 , 0.00548983, 0.00154646, 0.00039214])
[20]:
res_h.resid[:10]
[20]:
array([ 1.10849337, 1.10830496, -0.89188344, -0.89207183, 1.10773978,
-0.8924486 , -0.89263697, 0.10717466, 0.1069863 , 0.10679794])
[ ]: