估计后概述 - 泊松

此笔记本提供了在几种模型中可用的估计后结果概述，并以泊松模型为例进行说明。

另请参见 https://github.com/statsmodels/statsmodels/issues/7707

传统上，模型的结果类提供了沃尔德推断和预测。现在，几个模型在估计后结果方面具有额外的用于推断、预测和规范或诊断测试的方法。

以下是目前针对 tsa 之外的大多数最大似然模型（主要针对离散模型）的模式。其他模型在某种程度上仍然遵循不同的 API 模式。像 OLS 和 WLS 这样的线性模型有其特殊的实现，例如 OLS 影响。GLM 还有一些模型特有的功能。

主要估计后功能包括

  • 推断 - 沃尔德检验 部分

  • 推断 - 分数检验 部分

  • get_prediction 具有推断统计信息的预测 部分

  • get_distribution 基于估计参数的分布类 部分

  • get_diagnostic 诊断和规范检验、度量和图 部分

  • get_influence 异常值和影响诊断 部分

**警告** 最近添加的功能并不稳定。
主要功能已经过单元测试，并针对其他统计软件包进行了验证。但是，并非每个选项都经过了全面测试。随着添加更多功能，API、选项、默认值和返回类型可能仍然会发生变化。（当前重点是添加功能，而不是寻找方便且面向未来的接口。）

模拟示例

为了说明，我们为泊松回归模拟了数据，该数据指定正确，并且具有相对较大的样本。一个回归量是具有两个级别的分类变量。第二个回归量在单位区间内均匀分布。

[1]:

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

from statsmodels.discrete.discrete_model import Poisson
from statsmodels.discrete.diagnostic import PoissonDiagnostic

[2]:

np.random.seed(983154356)

nr = 10
n_groups = 2
labels = np.arange(n_groups)
x = np.repeat(labels, np.array([40, 60]) * nr)
nobs = x.shape[0]
exog = (x[:, None] == labels).astype(np.float64)
xc = np.random.rand(len(x))
exog = np.column_stack((exog, xc))
# reparameterize to explicit constant
# exog[:, 1] = 1
beta = np.array([0.2, 0.3, 0.5], np.float64)

linpred = exog @ beta
mean = np.exp(linpred)
y = np.random.poisson(mean)
len(y), y.mean(), (y == 0).mean()

res = Poisson(y, exog).fit(disp=0)
print(res.summary())

                          Poisson Regression Results
==============================================================================
Dep. Variable:                      y   No. Observations:                 1000
Model:                        Poisson   Df Residuals:                      997
Method:                           MLE   Df Model:                            2
Date:                Thu, 03 Oct 2024   Pseudo R-squ.:                 0.01258
Time:                        15:46:52   Log-Likelihood:                -1618.3
converged:                       True   LL-Null:                       -1638.9
Covariance Type:            nonrobust   LLR p-value:                 1.120e-09
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
x1             0.2386      0.061      3.926      0.000       0.120       0.358
x2             0.3229      0.055      5.873      0.000       0.215       0.431
x3             0.5109      0.083      6.186      0.000       0.349       0.673
==============================================================================

[ ]:

推断 - 沃尔德

沃尔德检验和其他基于沃尔德检验的推断统计量（如置信区间）一直是模型自始至终的功能。沃尔德推断基于在估计参数处评估的海森矩阵或预期信息矩阵。
参数的协方差矩阵可选地采用三明治形式，这对于未指定的异方差性或序列或簇相关性是稳健的（cov_type 选项用于 fit）。

除了参数表中的统计量之外，当前可用的方法是

  • t_test

  • wald_test

  • t_test_pairwise

  • wald_test_terms

f_test 可用作传统方法。它与具有关键字选项 use_f=True 的 wald_test 相同。

[3]:

res.t_test("x1=x2")

[3]:

<class 'statsmodels.stats.contrast.ContrastResults'>
                             Test for Constraints
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
c0            -0.0843      0.049     -1.717      0.086      -0.181       0.012
==============================================================================

[4]:

res.wald_test("x1=x2, x3", scalar=True)

[4]:

<class 'statsmodels.stats.contrast.ContrastResults'>
<Wald test (chi2): statistic=40.772322944293464, p-value=1.4008852592190214e-09, df_denom=2>

推断 - score_test

在 statsmodels 0.14 中针对大多数离散模型和 GLM 新增。

分数或拉格朗日乘子 (LM) 检验基于在零假设下估计的模型。一个常见的例子是变量添加检验，我们根据零限制估计模型参数，但根据完整模型评估分数和海森矩阵，以检验附加变量是否具有统计意义。

**注意：** 与沃尔德检验类似，在离散模型和 GLM 中实现的分数检验也有选择使用异方差性或相关性稳健协方差类型的选项。
它当前使用与沃尔德检验相同的实现和默认值来获得稳健协方差矩阵。在某些情况下，沃尔德检验中包含在 cov_type 中的小样本校正对于分数检验将不合适。在许多情况下，沃尔德检验过度拒绝，但分数检验可能会拒绝不足。将沃尔德小样本校正用于分数检验可能会导致更保守的 p 值。
（小样本校正的默认值将来可能会发生变化。目前关于异方差性和相关性稳健分数检验的小样本校正的信息很少。其他统计软件包仅针对少数特殊情况实现了它。）

我们可以使用变量添加 score_test 进行规范测试。在下面的例子中，我们测试模型中是否存在一些错误指定的非线性，方法是添加二次或多项式项。

在我们的例子中，我们可以预期这些规范检验不会拒绝零假设，因为模型指定正确，并且样本量很大。

[5]:

res.score_test(exog_extra=xc**2)

[5]:

(array([0.05300569]), array([0.81791332]), 1)
重置检验是针对连接函数正确规范的检验。检验的标准形式是在附加回归量中添加线性预测器的多项式项，并检验其显著性。这里，我们使用变量添加分数检验进行重置检验，其幂为 2 和 3。
[6]:

linpred = res.predict(which="linear")
res.score_test(exog_extra=linpred[:,None]**[2, 3])

[6]:

(array([1.3867703]), array([0.49988103]), 2)

预测

模型和结果类具有 predict 方法，它只返回预测值。 get_prediction 方法为预测、标准误差、p 值和置信区间添加推断统计信息。

对于以下示例，我们创建新的解释变量集，该变量集按分类级别划分，并在连续变量的均匀网格上划分。

[7]:

n = 11
exc = np.linspace(0, 1, n)
ex1 = np.column_stack((np.ones(n), np.zeros(n), exc))
ex2 = np.column_stack((np.zeros(n), np.ones(n), exc))

m1 = res.get_prediction(ex1)
m2 = res.get_prediction(ex2)

预测结果类中可用的方法和属性是

[8]:

[i for i in dir(m1) if not i.startswith("_")]

[8]:

['conf_int',
 'deriv',
 'df',
 'dist',
 'dist_args',
 'func',
 'linpred',
 'linpred_se',
 'predicted',
 'row_labels',
 'se',
 'summary_frame',
 't_test',
 'tvalues',
 'var_pred']

[9]:

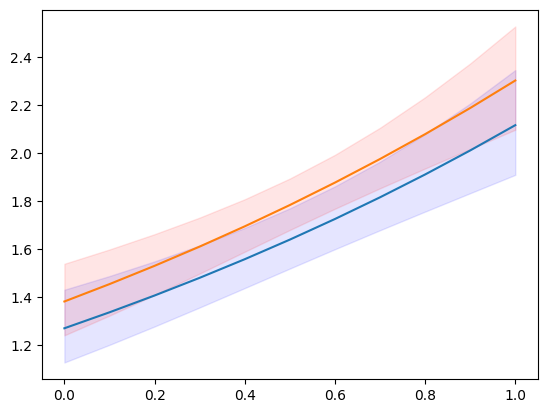
plt.plot(exc, np.column_stack([m1.predicted, m2.predicted]))
ci = m1.conf_int()
plt.fill_between(exc, ci[:, 0], ci[:, 1], color='b', alpha=.1)
ci = m2.conf_int()
plt.fill_between(exc, ci[:, 0], ci[:, 1], color='r', alpha=.1)
# to add observed points:
# y1 = y[x == 0]
# plt.plot(xc[x == 0], y1, ".", color="b", alpha=.3)
# y2 = y[x == 1]
# plt.plot(xc[x == 1], y2, ".", color="r", alpha=.3)

[9]:

<matplotlib.collections.PolyCollection at 0x7f852a5340a0>
../../../_images/examples_notebooks_generated_postestimation_poisson_16_1.png 
[10]:

y.max()

[10]:

np.int64(7)

我们可以预测的可用统计量之一（由“which”关键字指定）是预测分布的预期频率或概率。这向我们展示了对于给定的解释变量集，观察计数 = 1、2、3、… 的预测概率。

[11]:

y_max = 5
f1 = res.get_prediction(ex1, which="prob", y_values=np.arange(y_max + 1))
f2 = res.get_prediction(ex2, which="prob", y_values=np.arange(y_max + 1))
f1.predicted.mean(0), f2.predicted.mean(0)

[11]:

(array([0.19681697, 0.31325239, 0.25570764, 0.14275759, 0.06128168,
        0.02154715]),
 array([0.17115113, 0.29529781, 0.26128059, 0.15810937, 0.07357482,
        0.02804883]))

我们也可以获得预测概率的置信区间。但是，如果我们想要平均预测概率的置信区间，那么我们需要在预测函数内部进行聚合。相关的关键字是“average”，它计算由 exog 数组给出的观察结果的预测平均值。

[12]:

f1 = res.get_prediction(ex1, which="prob", y_values=np.arange(y_max + 1), average=True)
f2 = res.get_prediction(ex2, which="prob", y_values=np.arange(y_max + 1), average=True)
f1.predicted, f2.predicted

[12]:

(array([0.19681697, 0.31325239, 0.25570764, 0.14275759, 0.06128168,
        0.02154715]),
 array([0.17115113, 0.29529781, 0.26128059, 0.15810937, 0.07357482,
        0.02804883]))

[13]:

f1.conf_int()

[13]:

array([[0.17256941, 0.22106453],
       [0.2982307 , 0.32827408],
       [0.24818616, 0.26322912],
       [0.12876732, 0.15674787],
       [0.05088296, 0.07168041],
       [0.01626921, 0.0268251 ]])

[14]:

f2.conf_int()

[14]:

array([[0.15303084, 0.18927142],
       [0.28178041, 0.30881522],
       [0.25622062, 0.26634055],
       [0.14720224, 0.1690165 ],
       [0.06442055, 0.0827291 ],
       [0.02287077, 0.03322688]])
要获取有关预测方法和可用选项的更多信息，请参阅
help(res.get_prediction)
help(res.model.predict)

分布

对于给定的参数，我们可以创建一个 scipy 或 scipy 兼容的分布类实例。这使我们可以访问分布中的任何方法，pmf/pdf、cdf、stats。

结果类的 get_distribution 方法使用提供的解释变量数组和估计参数来指定向量化分布。模型的 get_prediction 方法可用于用户指定的参数 params。

[15]:

distr = res.get_distribution()
distr

[15]:

<scipy.stats._distn_infrastructure.rv_discrete_frozen at 0x7f852a592e30>

[16]:

distr.pmf(0)[:10]

[16]:

array([0.15420516, 0.13109359, 0.17645042, 0.16735421, 0.13445031,
       0.14851843, 0.22287053, 0.14979318, 0.25252986, 0.25013583])

条件分布的均值与模型的预测均值相同。

[17]:

distr.mean()[:10]

[17]:

array([1.86947133, 2.03184379, 1.73471534, 1.78764267, 2.00656061,
       1.90704623, 1.50116427, 1.89849971, 1.37622577, 1.3857512 ])

[18]:

res.predict()[:10]

[18]:

array([1.86947133, 2.03184379, 1.73471534, 1.78764267, 2.00656061,
       1.90704623, 1.50116427, 1.89849971, 1.37622577, 1.3857512 ])

我们也可以获得一组新的解释变量的分布。解释变量的提供方式与预测方法相同。

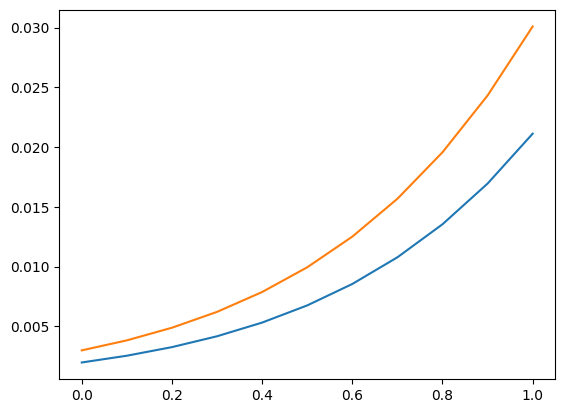
我们再次使用预测部分中的解释变量网格。作为其用法的示例，我们可以计算条件计数（严格）大于 5 的概率，该概率根据解释变量的值确定。

[19]:

distr1 = res.get_distribution(ex1)
distr2 = res.get_distribution(ex2)

[20]:

distr1.sf(5), distr2.sf(5)

[20]:

(array([0.00198421, 0.00255027, 0.00326858, 0.00417683, 0.00532093,
        0.00675641, 0.00854998, 0.01078116, 0.0135439 , 0.01694825,
        0.02112179]),
 array([0.00299758, 0.00383456, 0.00489029, 0.00621677, 0.00787663,
        0.00994468, 0.01250966, 0.01567579, 0.01956437, 0.02431503,
        0.03008666]))

[21]:

plt.plot(exc, np.column_stack([distr1.sf(5), distr2.sf(5)]))

[21]:

[<matplotlib.lines.Line2D at 0x7f852a42cb50>,
 <matplotlib.lines.Line2D at 0x7f852a42cc40>]
../../../_images/examples_notebooks_generated_postestimation_poisson_34_1.png

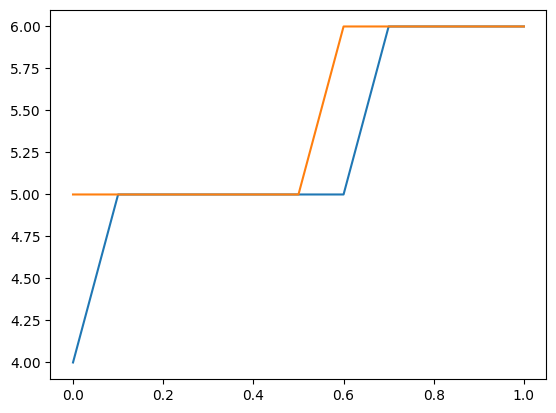
我们还可以使用分布来查找新观察结果的上置信限。以下图和表显示了给定解释变量的上限计数。观察此计数或更小计数的概率至少为 0.99。

请注意，这将参数视为固定，并未考虑参数的不确定性。

[22]:

plt.plot(exc, np.column_stack([distr1.ppf(0.99), distr2.ppf(0.99)]))

[22]:

[<matplotlib.lines.Line2D at 0x7f852a536140>,
 <matplotlib.lines.Line2D at 0x7f852a5358a0>]
../../../_images/examples_notebooks_generated_postestimation_poisson_36_1.png 
[23]:

[distr1.ppf(0.99), distr2.ppf(0.99)]

[23]:

[array([4., 5., 5., 5., 5., 5., 5., 6., 6., 6., 6.]),
 array([5., 5., 5., 5., 5., 5., 6., 6., 6., 6., 6.])]

诊断

泊松是第一个具有诊断类的模型，该模型可以通过 get_diagnostic 从结果中获得。其他计数模型具有通用的计数诊断类，该类目前仅具有有限数量的方法。

我们示例中的泊松模型指定正确。此外，我们的样本量很大。因此，在这种情况下，没有一个诊断检验会拒绝正确规范的零假设。

[24]:

dia = res.get_diagnostic()
[i for i in dir(dia) if not i.startswith("_")]

[24]:

['plot_probs',
 'probs_predicted',
 'results',
 'test_chisquare_prob',
 'test_dispersion',
 'test_poisson_zeroinflation',
 'y_max']

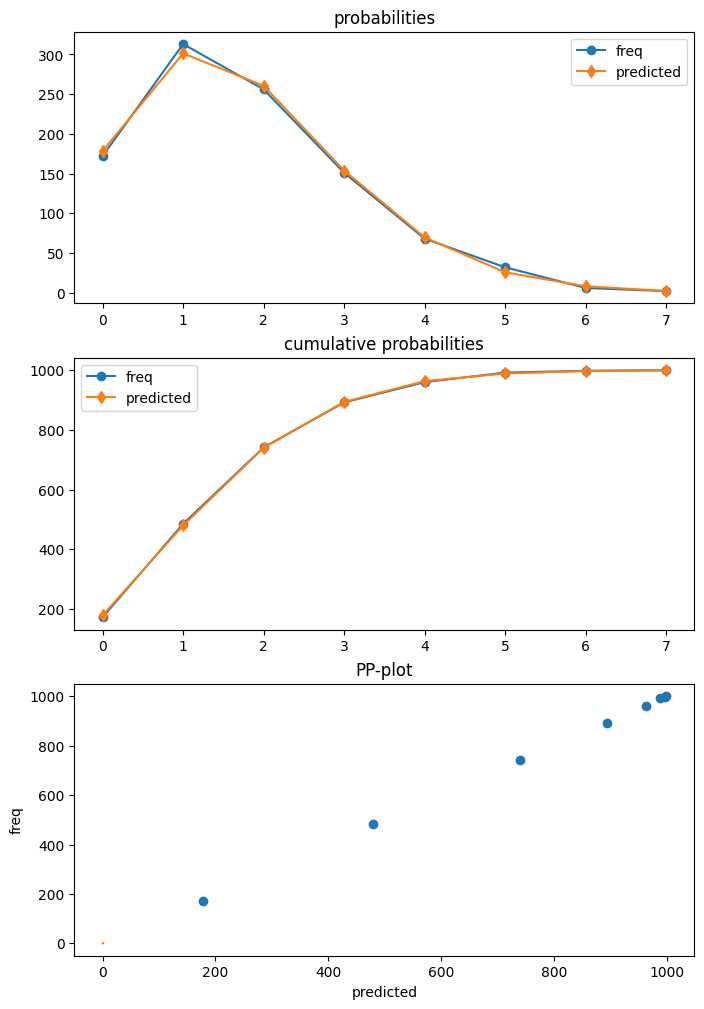
[25]:

dia.plot_probs();
../../../_images/examples_notebooks_generated_postestimation_poisson_40_0.png

测试过度分散

泊松有几种分散检验可用。目前，所有这些都已返回。DispersionResults 类有一个 summary_frame 方法。返回的数据框提供了结果概述，更易于阅读。

[26]:

td = dia.test_dispersion()
td

[26]:

<class 'statsmodels.discrete._diagnostics_count.DispersionResults'>
statistic = array([-0.42597379, -0.42597379, -0.39884024, -0.48327447, -0.48327447,
           -0.47790855, -0.45225818])
pvalue = array([0.67012695, 0.67012695, 0.69001092, 0.62890087, 0.62890087,
           0.6327153 , 0.651083  ])
method = ['Dean A', 'Dean B', 'Dean C', 'CT nb2', 'CT nb1', 'CT nb2 HC3', 'CT nb1 HC3']
alternative = ['mu (1 + a mu)', 'mu (1 + a mu)', 'mu (1 + a)', 'mu (1 + a mu)', 'mu (1 + a)', 'mu (1 + a mu)', 'mu (1 + a)']
name = 'Poisson Dispersion Test'
tuple = (array([-0.42597379, -0.42597379, -0.39884024, -0.48327447, -0.48327447,
           -0.47790855, -0.45225818]), array([0.67012695, 0.67012695, 0.69001092, 0.62890087, 0.62890087,
           0.6327153 , 0.651083  ]))

[27]:

df = td.summary_frame()
df

[27]:
统计量 p 值 方法 备择方案
0 -0.425974 0.670127 Dean A mu (1 + a mu)
1 -0.425974 0.670127 Dean B mu (1 + a mu)
2 -0.398840 0.690011 Dean C mu (1 + a)
3 -0.483274 0.628901 CT nb2 mu (1 + a mu)
4 -0.483274 0.628901 CT nb1 mu (1 + a)
5 -0.477909 0.632715 CT nb2 HC3 mu (1 + a mu)
6 -0.452258 0.651083 CT nb1 HC3 mu (1 + a)

测试零膨胀

[28]:

dia.test_poisson_zeroinflation()

[28]:

<class 'statsmodels.stats.base.HolderTuple'>
statistic = np.float64(-0.6657556201098714)
pvalue = np.float64(0.5055673158225651)
pvalue_smaller = np.float64(0.7472163420887175)
pvalue_larger = np.float64(0.25278365791128254)
chi2 = np.float64(0.44323054570787945)
pvalue_chi2 = np.float64(0.505567315822565)
df_chi2 = 1
distribution = 'normal'
tuple = (np.float64(-0.6657556201098714), np.float64(0.5055673158225651))

零膨胀的卡方检验

[29]:

dia.test_chisquare_prob(bin_edges=np.arange(3))

[29]:

<class 'statsmodels.stats.base.HolderTuple'>
statistic = np.float64(0.456170941873113)
pvalue = np.float64(0.4994189468121014)
df = np.int64(1)
diff1 = array([[-0.15420516,  0.71171787],
           [-0.13109359, -0.26636169],
           [-0.17645042, -0.30609125],
           ...,
           [-0.10477112, -0.23636125],
           [-0.10675436, -0.2388335 ],
           [-0.21168332, -0.32867305]])
res_aux = <statsmodels.regression.linear_model.RegressionResultsWrapper object at 0x7f852a290eb0>
distribution = 'chi2'
tuple = (np.float64(0.456170941873113), np.float64(0.4994189468121014))

预测频率的拟合优度检验

这是一个卡方检验，它考虑了参数是估计的。大于最大 bin 边缘的计数将添加到最后一个 bin，以便 bin 的总和为 1。

例如，使用 5 个 bin

[30]:

dt = dia.test_chisquare_prob(bin_edges=np.arange(6))
dt

[30]:

<class 'statsmodels.stats.base.HolderTuple'>
statistic = np.float64(0.9414641297779136)
pvalue = np.float64(0.9185382008345917)
df = np.int64(4)
diff1 = array([[-0.15420516,  0.71171787, -0.26946759, -0.16792064, -0.07848071],
           [-0.13109359, -0.26636169, -0.27060268,  0.81672588, -0.0930961 ],
           [-0.17645042, -0.30609125,  0.7345094 , -0.15351687, -0.06657702],
           ...,
           [-0.10477112, -0.23636125, -0.26661279,  0.79950922, -0.11307565],
           [-0.10675436, -0.2388335 ,  0.73283789, -0.1992339 , -0.11143275],
           [-0.21168332, -0.32867305,  0.74484061, -0.13205892, -0.05126078]])
res_aux = <statsmodels.regression.linear_model.RegressionResultsWrapper object at 0x7f852a27a7d0>
distribution = 'chi2'
tuple = (np.float64(0.9414641297779136), np.float64(0.9185382008345917))

[31]:

dt.diff1.mean(0)

[31]:

array([-0.00628136,  0.01177308, -0.00449604, -0.00270524, -0.00156519])

[32]:

vars(dia)

[32]:

{'results': <statsmodels.discrete.discrete_model.PoissonResults at 0x7f85761bdcf0>,
 'y_max': None,
 '_cache': {'probs_predicted': array([[0.15420516, 0.28828213, 0.26946759, ..., 0.02934349, 0.0091428 ,
          0.00244174],
         [0.13109359, 0.26636169, 0.27060268, ..., 0.03783135, 0.01281123,
          0.00371863],
         [0.17645042, 0.30609125, 0.2654906 , ..., 0.02309843, 0.0066782 ,
          0.00165497],
         ...,
         [0.10477112, 0.23636125, 0.26661279, ..., 0.05101921, 0.01918303,
          0.00618235],
         [0.10675436, 0.2388335 , 0.26716211, ..., 0.04986002, 0.01859135,
          0.00594186],
         [0.21168332, 0.32867305, 0.25515939, ..., 0.01591815, 0.00411926,
          0.00091369]])}}

异常值和影响

Statsmodels 为非线性模型（期望均值非线性的模型）提供了通用 MLEInfluence 类，这些模型适用于离散模型和其他基于最大似然的模型，例如 Beta 回归模型。提供的度量基于通用定义，例如广义杠杆率，而不是线性模型中帽子矩阵的对角线。

结果方法 get_influence 返回 MLEInfluence 类的实例，该实例具有各种用于异常值和影响度量的方法。

[33]:

infl = res.get_influence()
[i for i in dir(infl) if not i.startswith("_")]

[33]:

['cooks_distance',
 'cov_params',
 'd_fittedvalues',
 'd_fittedvalues_scaled',
 'd_params',
 'dfbetas',
 'endog',
 'exog',
 'hat_matrix_diag',
 'hat_matrix_exog_diag',
 'hessian',
 'k_params',
 'k_vars',
 'model_class',
 'nobs',
 'params_one',
 'plot_index',
 'plot_influence',
 'resid',
 'resid_score',
 'resid_score_factor',
 'resid_studentized',
 'results',
 'scale',
 'score_obs',
 'summary_frame']

影响类有两个绘图方法。但是，由于样本量很大，这些图在这种情况下过于拥挤。

[34]:

infl.plot_influence();
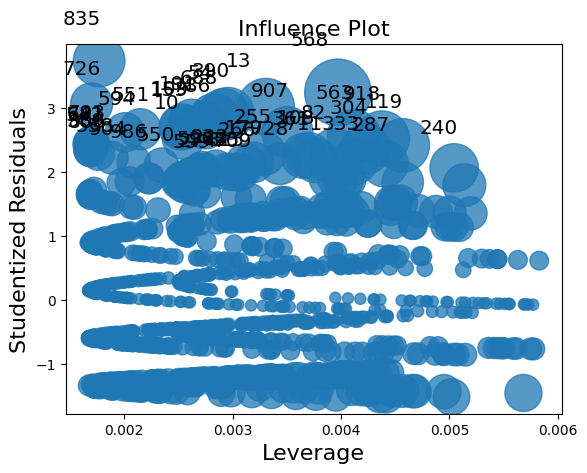
../../../_images/examples_notebooks_generated_postestimation_poisson_55_0.png 
[35]:

infl.plot_index(y_var="resid_studentized");
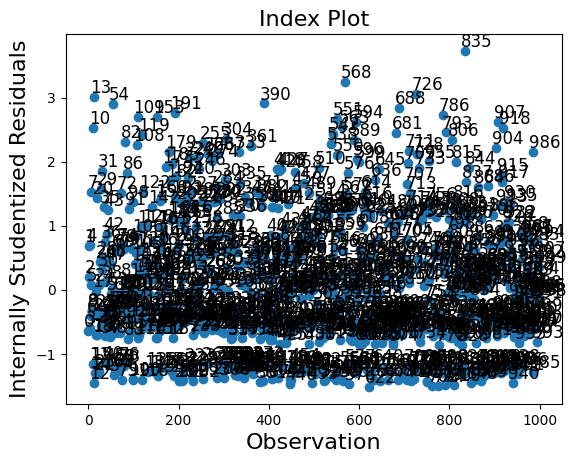
../../../_images/examples_notebooks_generated_postestimation_poisson_56_0.png

一个 summary_frame 显示了每个观测值的 主要影响 和 异常值度量。

我们的示例中有 1000 个观测值，太多了，无法轻松显示。我们可以按其中一列对摘要数据框进行排序，并列出具有最大异常值或影响度量的观测值。在下面的示例中，我们按 Cook 的距离和 standard_resid 进行排序，在一般情况下，它是 Pearson 残差。

因为我们模拟了一个“良好”模型，所以没有观察到具有较大影响或为较大异常值的观测值。

[36]:

df_infl = infl.summary_frame()
df_infl.head()

[36]:
dfb_x1 dfb_x2 dfb_x3 cooks_d standard_resid hat_diag dffits_internal
0 -0.010856 0.011384 -0.013643 0.000440 -0.636944 0.003243 -0.036334
1 0.001990 -0.023625 0.028313 0.000737 0.680823 0.004749 0.047031
2 0.005794 -0.000787 0.000943 0.000035 0.201681 0.002607 0.010311
3 -0.014243 0.005539 -0.006639 0.000325 -0.589923 0.002790 -0.031206
4 0.003602 -0.022549 0.027024 0.000738 0.702888 0.004462 0.047057 
[37]:

df_infl.sort_values("cooks_d", ascending=False)[:10]

[37]:
dfb_x1 dfb_x2 dfb_x3 cooks_d standard_resid hat_diag dffits_internal
568 -0.110520 -0.038997 0.143106 0.013922 3.236167 0.003972 0.204365
13 0.048914 -0.056713 0.067969 0.010034 3.011778 0.003307 0.173497
918 -0.093971 -0.038431 0.121677 0.009304 2.519367 0.004378 0.167066
563 -0.089917 -0.033708 0.116428 0.008935 2.545624 0.004119 0.163720
119 0.163230 0.103957 -0.124589 0.008883 2.409646 0.004569 0.163247
390 0.148697 0.066972 -0.080264 0.008358 2.907190 0.002958 0.158345
835 -0.017672 0.066475 0.022883 0.008209 3.727645 0.001769 0.156931
54 0.145944 0.064216 -0.076961 0.008156 2.892554 0.002916 0.156419
907 -0.078901 -0.020908 0.102164 0.008021 2.615676 0.003505 0.155126
304 0.152905 0.093680 -0.112272 0.007821 2.351520 0.004225 0.153179 
[38]:

df_infl.sort_values("standard_resid", ascending=False)[:10]

[38]:
dfb_x1 dfb_x2 dfb_x3 cooks_d standard_resid hat_diag dffits_internal
835 -0.017672 0.066475 0.022883 0.008209 3.727645 0.001769 0.156931
568 -0.110520 -0.038997 0.143106 0.013922 3.236167 0.003972 0.204365
726 -0.003941 0.065200 0.005103 0.005303 3.056406 0.001700 0.126127
13 0.048914 -0.056713 0.067969 0.010034 3.011778 0.003307 0.173497
390 0.148697 0.066972 -0.080264 0.008358 2.907190 0.002958 0.158345
54 0.145944 0.064216 -0.076961 0.008156 2.892554 0.002916 0.156419
688 0.083205 0.148254 -0.107737 0.007606 2.833988 0.002833 0.151057
191 0.122062 0.040388 -0.048403 0.006704 2.764369 0.002625 0.141815
786 -0.061179 -0.000408 0.079217 0.006827 2.724900 0.002751 0.143110
109 0.110999 0.029401 -0.035236 0.006212 2.704144 0.002542 0.136518
上次更新：2024 年 10 月 3 日