线性回归诊断¶
在现实生活中,响应变量和目标变量之间的关系很少是线性的。在这里,我们利用 statsmodels 的输出可视化并识别将 线性 回归 模型拟合到非线性关系时可能出现的潜在问题。主要目标是重现 James 等人著作的统计学习导论 (ISLR) 书籍中“潜在问题”部分 (第 3.3.3 章) 中讨论的可视化方法,Springer 出版。
[1]:
import statsmodels
import statsmodels.formula.api as smf
import pandas as pd
简单多元线性回归¶
首先,让我们从 ISLR 书籍的第 2 章加载广告数据并对其进行线性模型拟合。
[2]:
# Load data
data_url = "https://raw.githubusercontent.com/nguyen-toan/ISLR/07fd968ea484b5f6febc7b392a28eb64329a4945/dataset/Advertising.csv"
df = pd.read_csv(data_url).drop('Unnamed: 0', axis=1)
df.head()
[2]:
| 电视 | 广播 | 报纸 | 销售额 | |
|---|---|---|---|---|
| 0 | 230.1 | 37.8 | 69.2 | 22.1 |
| 1 | 44.5 | 39.3 | 45.1 | 10.4 |
| 2 | 17.2 | 45.9 | 69.3 | 9.3 |
| 3 | 151.5 | 41.3 | 58.5 | 18.5 |
| 4 | 180.8 | 10.8 | 58.4 | 12.9 |
[3]:
# Fitting linear model
res = smf.ols(formula= "Sales ~ TV + Radio + Newspaper", data=df).fit()
res.summary()
[3]:
| 因变量 | 销售额 | R 平方 | 0.897 |
|---|---|---|---|
| 模型 | OLS | 调整后的 R 平方 | 0.896 |
| 方法 | 最小二乘法 | F 统计量 | 570.3 |
| 日期 | Thu, 03 Oct 2024 | Prob (F 统计量) | 1.58e-96 |
| 时间 | 15:45:11 | 对数似然 | -386.18 |
| 观测数量 | 200 | AIC | 780.4 |
| 残差自由度 | 196 | BIC | 793.6 |
| 模型自由度 | 3 | ||
| 协方差类型 | 非鲁棒 |
| 系数 | 标准误 | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 截距 | 2.9389 | 0.312 | 9.422 | 0.000 | 2.324 | 3.554 |
| 电视 | 0.0458 | 0.001 | 32.809 | 0.000 | 0.043 | 0.049 |
| 广播 | 0.1885 | 0.009 | 21.893 | 0.000 | 0.172 | 0.206 |
| 报纸 | -0.0010 | 0.006 | -0.177 | 0.860 | -0.013 | 0.011 |
| Omnibus | 60.414 | Durbin-Watson | 2.084 |
|---|---|---|---|
| Prob(Omnibus) | 0.000 | Jarque-Bera (JB) | 151.241 |
| 偏度 | -1.327 | Prob(JB) | 1.44e-33 |
| 峰度 | 6.332 | 条件数 | 454. |
注释
[1] 标准误假设误差的协方差矩阵是正确指定的。
诊断图形/表格¶
在下面,我们首先给出基本代码,我们稍后将使用该代码来生成以下诊断图
a. residual
b. qq
c. scale location
d. leverage
和表格
a. vif
[4]:
# base code
import numpy as np
import seaborn as sns
from statsmodels.tools.tools import maybe_unwrap_results
from statsmodels.graphics.gofplots import ProbPlot
from statsmodels.stats.outliers_influence import variance_inflation_factor
import matplotlib.pyplot as plt
from typing import Type
style_talk = 'seaborn-talk' #refer to plt.style.available
class LinearRegDiagnostic():
"""
Diagnostic plots to identify potential problems in a linear regression fit.
Mainly,
a. non-linearity of data
b. Correlation of error terms
c. non-constant variance
d. outliers
e. high-leverage points
f. collinearity
Authors:
Prajwal Kafle (p33ajkafle@gmail.com, where 3 = r)
Does not come with any sort of warranty.
Please test the code one your end before using.
Matt Spinelli (m3spinelli@gmail.com, where 3 = r)
(1) Fixed incorrect annotation of the top most extreme residuals in
the Residuals vs Fitted and, especially, the Normal Q-Q plots.
(2) Changed Residuals vs Leverage plot to match closer the y-axis
range shown in the equivalent plot in the R package ggfortify.
(3) Added horizontal line at y=0 in Residuals vs Leverage plot to
match the plots in R package ggfortify and base R.
(4) Added option for placing a vertical guideline on the Residuals
vs Leverage plot using the rule of thumb of h = 2p/n to denote
high leverage (high_leverage_threshold=True).
(5) Added two more ways to compute the Cook's Distance (D) threshold:
* 'baseR': D > 1 and D > 0.5 (default)
* 'convention': D > 4/n
* 'dof': D > 4 / (n - k - 1)
(6) Fixed class name to conform to Pascal casing convention
(7) Fixed Residuals vs Leverage legend to work with loc='best'
"""
def __init__(self,
results: Type[statsmodels.regression.linear_model.RegressionResultsWrapper]) -> None:
"""
For a linear regression model, generates following diagnostic plots:
a. residual
b. qq
c. scale location and
d. leverage
and a table
e. vif
Args:
results (Type[statsmodels.regression.linear_model.RegressionResultsWrapper]):
must be instance of statsmodels.regression.linear_model object
Raises:
TypeError: if instance does not belong to above object
Example:
>>> import numpy as np
>>> import pandas as pd
>>> import statsmodels.formula.api as smf
>>> x = np.linspace(-np.pi, np.pi, 100)
>>> y = 3*x + 8 + np.random.normal(0,1, 100)
>>> df = pd.DataFrame({'x':x, 'y':y})
>>> res = smf.ols(formula= "y ~ x", data=df).fit()
>>> cls = Linear_Reg_Diagnostic(res)
>>> cls(plot_context="seaborn-v0_8-paper")
In case you do not need all plots you can also independently make an individual plot/table
in following ways
>>> cls = Linear_Reg_Diagnostic(res)
>>> cls.residual_plot()
>>> cls.qq_plot()
>>> cls.scale_location_plot()
>>> cls.leverage_plot()
>>> cls.vif_table()
"""
if isinstance(results, statsmodels.regression.linear_model.RegressionResultsWrapper) is False:
raise TypeError("result must be instance of statsmodels.regression.linear_model.RegressionResultsWrapper object")
self.results = maybe_unwrap_results(results)
self.y_true = self.results.model.endog
self.y_predict = self.results.fittedvalues
self.xvar = self.results.model.exog
self.xvar_names = self.results.model.exog_names
self.residual = np.array(self.results.resid)
influence = self.results.get_influence()
self.residual_norm = influence.resid_studentized_internal
self.leverage = influence.hat_matrix_diag
self.cooks_distance = influence.cooks_distance[0]
self.nparams = len(self.results.params)
self.nresids = len(self.residual_norm)
def __call__(self, plot_context='seaborn-v0_8-paper', **kwargs):
# print(plt.style.available)
with plt.style.context(plot_context):
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(10,10))
self.residual_plot(ax=ax[0,0])
self.qq_plot(ax=ax[0,1])
self.scale_location_plot(ax=ax[1,0])
self.leverage_plot(
ax=ax[1,1],
high_leverage_threshold = kwargs.get('high_leverage_threshold'),
cooks_threshold = kwargs.get('cooks_threshold'))
plt.show()
return self.vif_table(), fig, ax,
def residual_plot(self, ax=None):
"""
Residual vs Fitted Plot
Graphical tool to identify non-linearity.
(Roughly) Horizontal red line is an indicator that the residual has a linear pattern
"""
if ax is None:
fig, ax = plt.subplots()
sns.residplot(
x=self.y_predict,
y=self.residual,
lowess=True,
scatter_kws={'alpha': 0.5},
line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8},
ax=ax)
# annotations
residual_abs = np.abs(self.residual)
abs_resid = np.flip(np.argsort(residual_abs), 0)
abs_resid_top_3 = abs_resid[:3]
for i in abs_resid_top_3:
ax.annotate(
i,
xy=(self.y_predict[i], self.residual[i]),
color='C3')
ax.set_title('Residuals vs Fitted', fontweight="bold")
ax.set_xlabel('Fitted values')
ax.set_ylabel('Residuals')
return ax
def qq_plot(self, ax=None):
"""
Standarized Residual vs Theoretical Quantile plot
Used to visually check if residuals are normally distributed.
Points spread along the diagonal line will suggest so.
"""
if ax is None:
fig, ax = plt.subplots()
QQ = ProbPlot(self.residual_norm)
fig = QQ.qqplot(line='45', alpha=0.5, lw=1, ax=ax)
# annotations
abs_norm_resid = np.flip(np.argsort(np.abs(self.residual_norm)), 0)
abs_norm_resid_top_3 = abs_norm_resid[:3]
for i, x, y in self.__qq_top_resid(QQ.theoretical_quantiles, abs_norm_resid_top_3):
ax.annotate(
i,
xy=(x, y),
ha='right',
color='C3')
ax.set_title('Normal Q-Q', fontweight="bold")
ax.set_xlabel('Theoretical Quantiles')
ax.set_ylabel('Standardized Residuals')
return ax
def scale_location_plot(self, ax=None):
"""
Sqrt(Standarized Residual) vs Fitted values plot
Used to check homoscedasticity of the residuals.
Horizontal line will suggest so.
"""
if ax is None:
fig, ax = plt.subplots()
residual_norm_abs_sqrt = np.sqrt(np.abs(self.residual_norm))
ax.scatter(self.y_predict, residual_norm_abs_sqrt, alpha=0.5);
sns.regplot(
x=self.y_predict,
y=residual_norm_abs_sqrt,
scatter=False, ci=False,
lowess=True,
line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8},
ax=ax)
# annotations
abs_sq_norm_resid = np.flip(np.argsort(residual_norm_abs_sqrt), 0)
abs_sq_norm_resid_top_3 = abs_sq_norm_resid[:3]
for i in abs_sq_norm_resid_top_3:
ax.annotate(
i,
xy=(self.y_predict[i], residual_norm_abs_sqrt[i]),
color='C3')
ax.set_title('Scale-Location', fontweight="bold")
ax.set_xlabel('Fitted values')
ax.set_ylabel(r'$\sqrt{|\mathrm{Standardized\ Residuals}|}$');
return ax
def leverage_plot(self, ax=None, high_leverage_threshold=False, cooks_threshold='baseR'):
"""
Residual vs Leverage plot
Points falling outside Cook's distance curves are considered observation that can sway the fit
aka are influential.
Good to have none outside the curves.
"""
if ax is None:
fig, ax = plt.subplots()
ax.scatter(
self.leverage,
self.residual_norm,
alpha=0.5);
sns.regplot(
x=self.leverage,
y=self.residual_norm,
scatter=False,
ci=False,
lowess=True,
line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8},
ax=ax)
# annotations
leverage_top_3 = np.flip(np.argsort(self.cooks_distance), 0)[:3]
for i in leverage_top_3:
ax.annotate(
i,
xy=(self.leverage[i], self.residual_norm[i]),
color = 'C3')
factors = []
if cooks_threshold == 'baseR' or cooks_threshold is None:
factors = [1, 0.5]
elif cooks_threshold == 'convention':
factors = [4/self.nresids]
elif cooks_threshold == 'dof':
factors = [4/ (self.nresids - self.nparams)]
else:
raise ValueError("threshold_method must be one of the following: 'convention', 'dof', or 'baseR' (default)")
for i, factor in enumerate(factors):
label = "Cook's distance" if i == 0 else None
xtemp, ytemp = self.__cooks_dist_line(factor)
ax.plot(xtemp, ytemp, label=label, lw=1.25, ls='--', color='red')
ax.plot(xtemp, np.negative(ytemp), lw=1.25, ls='--', color='red')
if high_leverage_threshold:
high_leverage = 2 * self.nparams / self.nresids
if max(self.leverage) > high_leverage:
ax.axvline(high_leverage, label='High leverage', ls='-.', color='purple', lw=1)
ax.axhline(0, ls='dotted', color='black', lw=1.25)
ax.set_xlim(0, max(self.leverage)+0.01)
ax.set_ylim(min(self.residual_norm)-0.1, max(self.residual_norm)+0.1)
ax.set_title('Residuals vs Leverage', fontweight="bold")
ax.set_xlabel('Leverage')
ax.set_ylabel('Standardized Residuals')
plt.legend(loc='best')
return ax
def vif_table(self):
"""
VIF table
VIF, the variance inflation factor, is a measure of multicollinearity.
VIF > 5 for a variable indicates that it is highly collinear with the
other input variables.
"""
vif_df = pd.DataFrame()
vif_df["Features"] = self.xvar_names
vif_df["VIF Factor"] = [variance_inflation_factor(self.xvar, i) for i in range(self.xvar.shape[1])]
return (vif_df
.sort_values("VIF Factor")
.round(2))
def __cooks_dist_line(self, factor):
"""
Helper function for plotting Cook's distance curves
"""
p = self.nparams
formula = lambda x: np.sqrt((factor * p * (1 - x)) / x)
x = np.linspace(0.001, max(self.leverage), 50)
y = formula(x)
return x, y
def __qq_top_resid(self, quantiles, top_residual_indices):
"""
Helper generator function yielding the index and coordinates
"""
offset = 0
quant_index = 0
previous_is_negative = None
for resid_index in top_residual_indices:
y = self.residual_norm[resid_index]
is_negative = y < 0
if previous_is_negative == None or previous_is_negative == is_negative:
offset += 1
else:
quant_index -= offset
x = quantiles[quant_index] if is_negative else np.flip(quantiles, 0)[quant_index]
quant_index += 1
previous_is_negative = is_negative
yield resid_index, x, y
利用
* fitted model on the Advertising data above and
* the base code provided
现在我们逐个生成诊断图。
[5]:
cls = LinearRegDiagnostic(res)
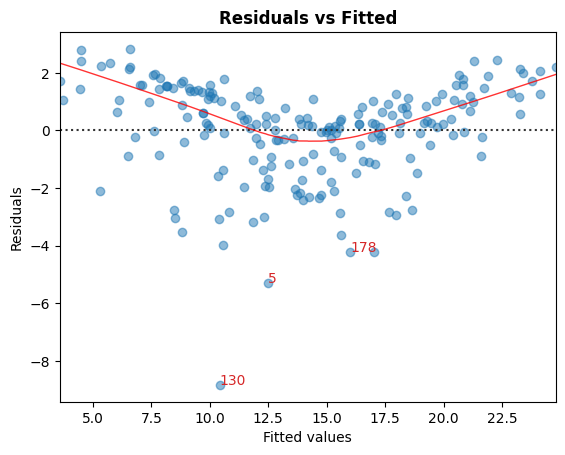
A. 残差与拟合值
识别非线性的图形工具。
在图中,红色的(大致)水平线表示残差具有线性模式。
[6]:
cls.residual_plot();
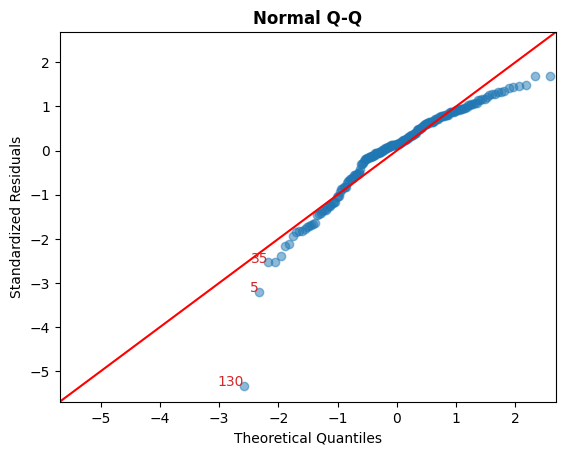
B. 标准化残差与理论分位数
此图用于直观检查残差是否呈正态分布。
沿对角线分布的点将表明这一点。
[7]:
cls.qq_plot();
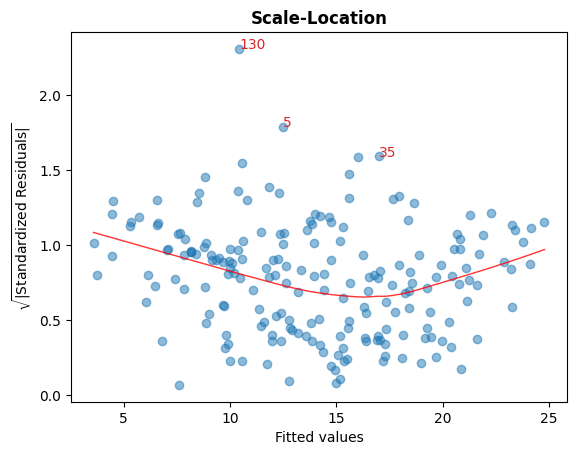
C. Sqrt(标准化残差) 与拟合值
此图用于检查残差的同方差性。
图中接近水平的红线表明这一点。
[8]:
cls.scale_location_plot();
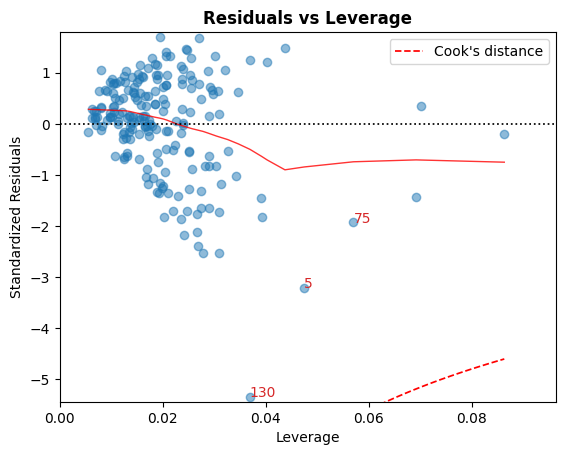
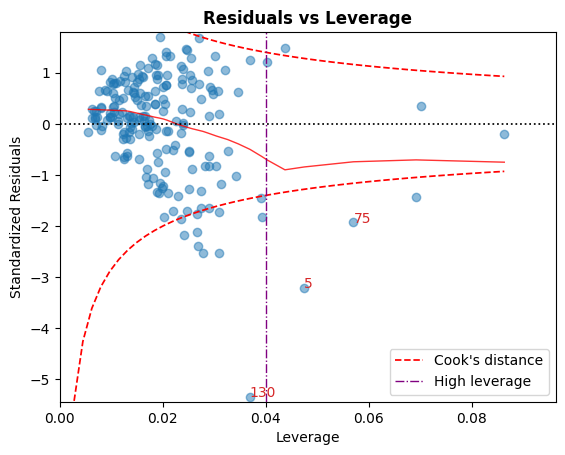
D. 残差与杠杆率
落在 Cook 距离曲线之外的点被认为是会影响拟合的观测值,也就是有影响力的观测值。
最好没有点落在这些曲线之外。
[9]:
cls.leverage_plot();
Cook 距离曲线可以使用其他经验法则绘制
经验法则 |
阈值 |
|---|---|
|
\[D_i > 1 \mid D_i > 0.5\]
|
|
\[D_i > { 4 \over n}\]
|
|
\[D_i > {4 \over n - k - 1}\]
|
高杠杆率准则也可以使用以下惯例显示:\(h_{ii} > {2p \over n}\).
[10]:
cls.leverage_plot(high_leverage_threshold=True, cooks_threshold='dof');
E. VIF
方差膨胀因子 (VIF) 是多重共线性的度量。
对于变量,如果 VIF > 5,则表示它与其他输入变量高度共线性。
[11]:
cls.vif_table()
[11]:
| 特征 | VIF 因子 | |
|---|---|---|
| 1 | 电视 | 1.00 |
| 2 | 广播 | 1.14 |
| 3 | 报纸 | 1.15 |
| 0 | 截距 | 6.85 |
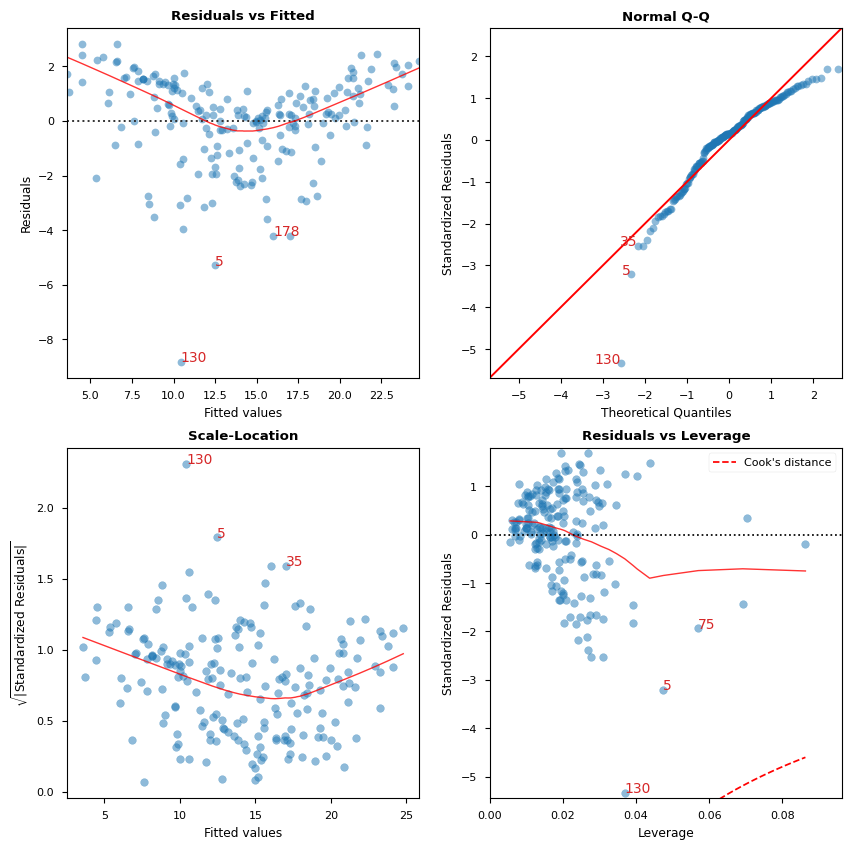
[12]:
# Alternatively, all diagnostics can be generated in one go as follows.
# Fig and ax can be used to modify axes or plot properties after the fact.
cls = LinearRegDiagnostic(res)
vif, fig, ax = cls()
print(vif)
#fig.savefig('../../docs/source/_static/images/linear_regression_diagnostics_plots.png')
Features VIF Factor
1 TV 1.00
2 Radio 1.14
3 Newspaper 1.15
0 Intercept 6.85
有关上述图的解释和注意事项的详细讨论,请参考 ISLR 书籍。
上次更新:2024 年 10 月 3 日