回归图¶
[1]:
%matplotlib inline
[2]:
from statsmodels.compat import lzip
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
邓肯的声望数据集¶
加载数据¶
我们可以使用一个实用程序函数来加载任何来自 Rdatasets 包的 R 数据集。
[3]:
prestige = sm.datasets.get_rdataset("Duncan", "carData", cache=True).data
[4]:
prestige.head()
[4]:
| 类型 | 收入 | 教育 | 声望 | |
|---|---|---|---|---|
| 行名 | ||||
| 会计 | 教授 | 62 | 86 | 82 |
| 飞行员 | 教授 | 72 | 76 | 83 |
| 建筑师 | 教授 | 75 | 92 | 90 |
| 作者 | 教授 | 55 | 90 | 76 |
| 化学家 | 教授 | 64 | 86 | 90 |
[5]:
prestige_model = ols("prestige ~ income + education", data=prestige).fit()
[6]:
print(prestige_model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: prestige R-squared: 0.828
Model: OLS Adj. R-squared: 0.820
Method: Least Squares F-statistic: 101.2
Date: Thu, 03 Oct 2024 Prob (F-statistic): 8.65e-17
Time: 15:58:25 Log-Likelihood: -178.98
No. Observations: 45 AIC: 364.0
Df Residuals: 42 BIC: 369.4
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -6.0647 4.272 -1.420 0.163 -14.686 2.556
income 0.5987 0.120 5.003 0.000 0.357 0.840
education 0.5458 0.098 5.555 0.000 0.348 0.744
==============================================================================
Omnibus: 1.279 Durbin-Watson: 1.458
Prob(Omnibus): 0.528 Jarque-Bera (JB): 0.520
Skew: 0.155 Prob(JB): 0.771
Kurtosis: 3.426 Cond. No. 163.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
影响图¶
影响图显示了(外部)学生化残差与每个观测值的杠杆率,该杠杆率由帽子矩阵测量。
外部学生化残差是按其标准差缩放的残差,其中
其中
\(n\) 是观测值的数目,\(p\) 是回归变量的数目。 \(h_{ii}\) 是帽子矩阵的第 \(i\) 个对角元素
每个点的影响可以通过 criterion 关键字参数可视化。选项包括 Cook 距离和 DFFITS,这是影响的两种度量。
[7]:
fig = sm.graphics.influence_plot(prestige_model, criterion="cooks")
fig.tight_layout(pad=1.0)
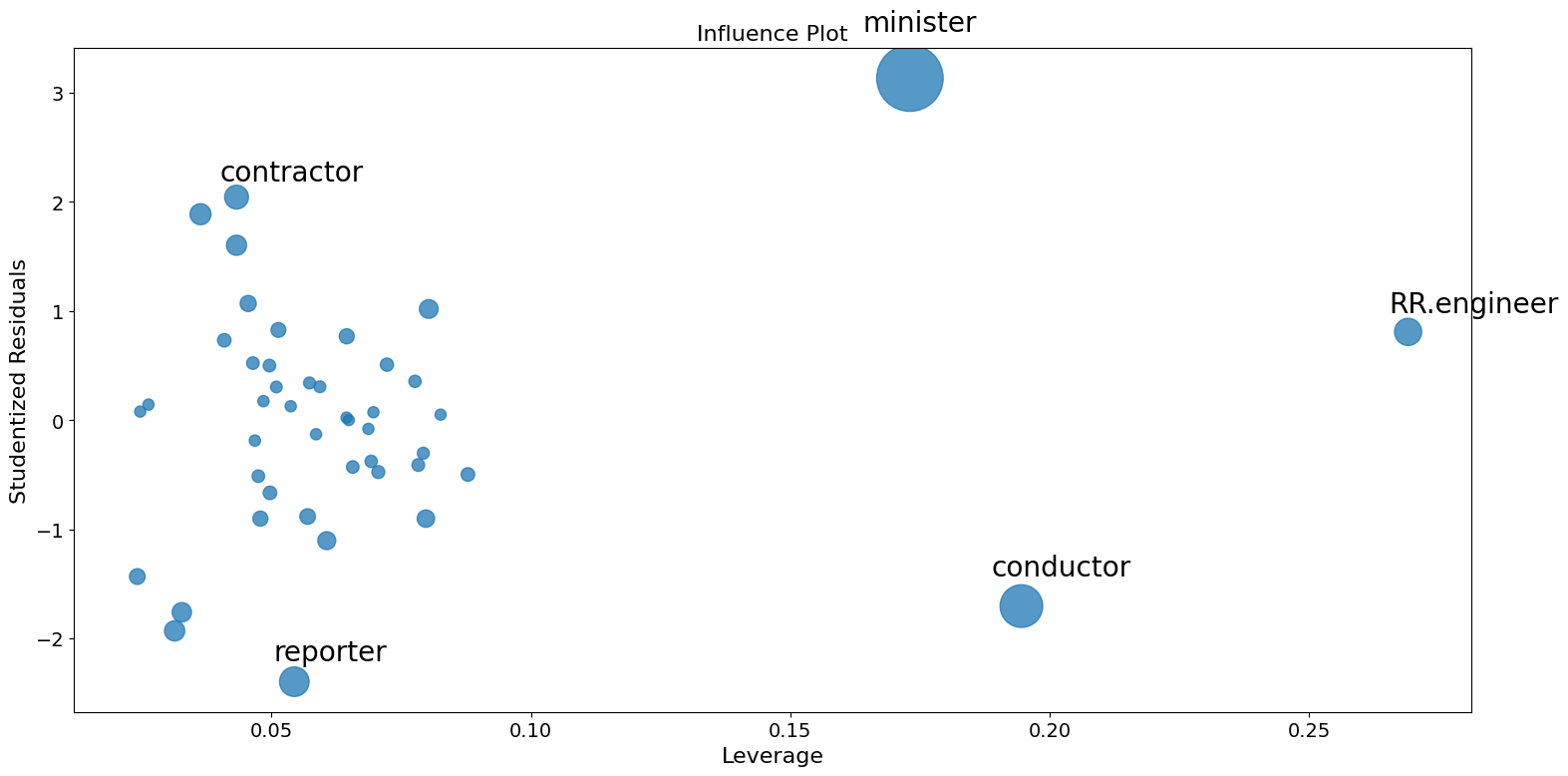
正如你所看到的,有一些令人担忧的观察结果。承包商和记者的杠杆率都很低,但残差很大。RR.engineer 的残差很小,杠杆率很大。指挥家和牧师既有高杠杆率又有大残差,因此影响很大。
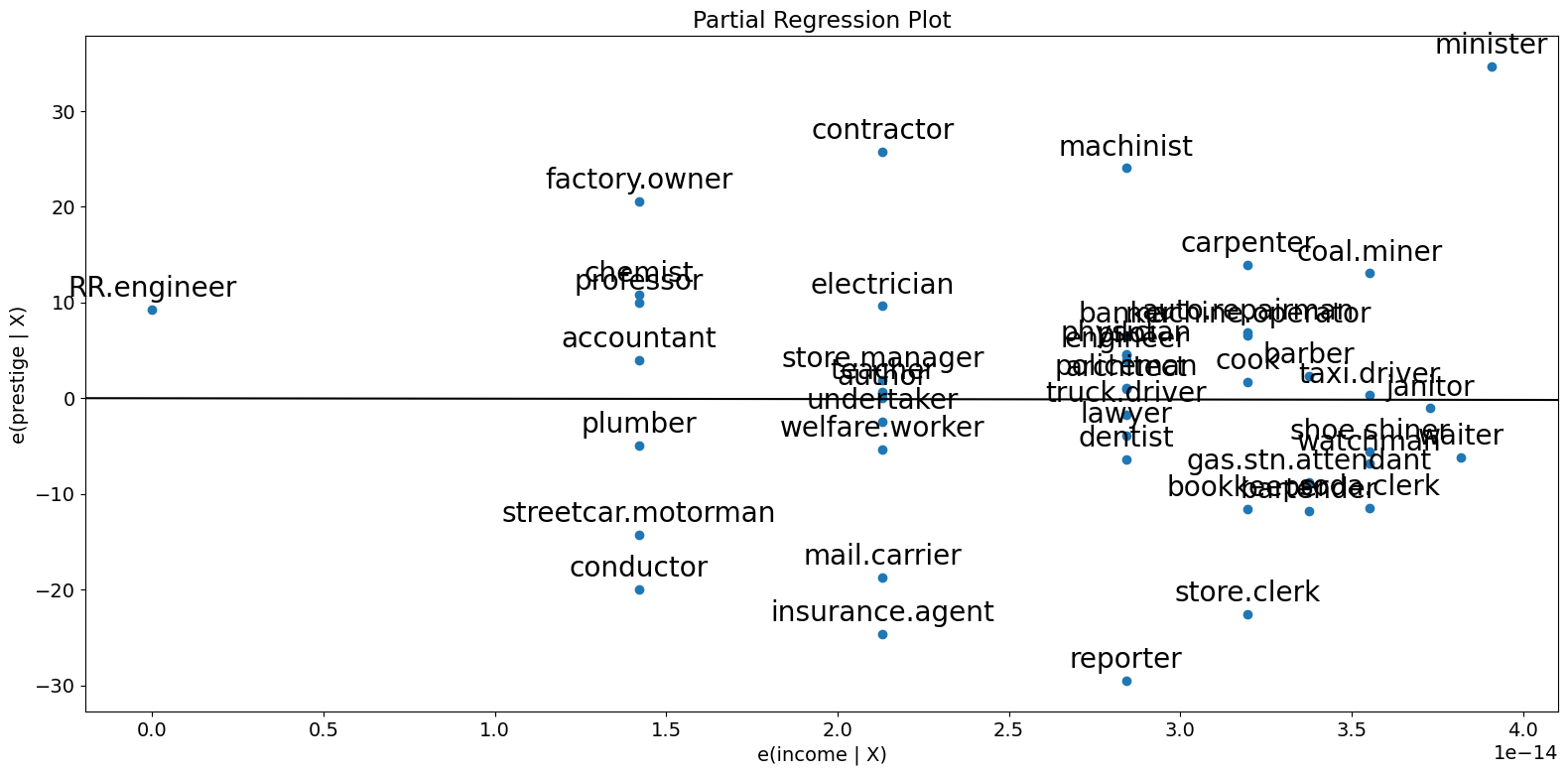
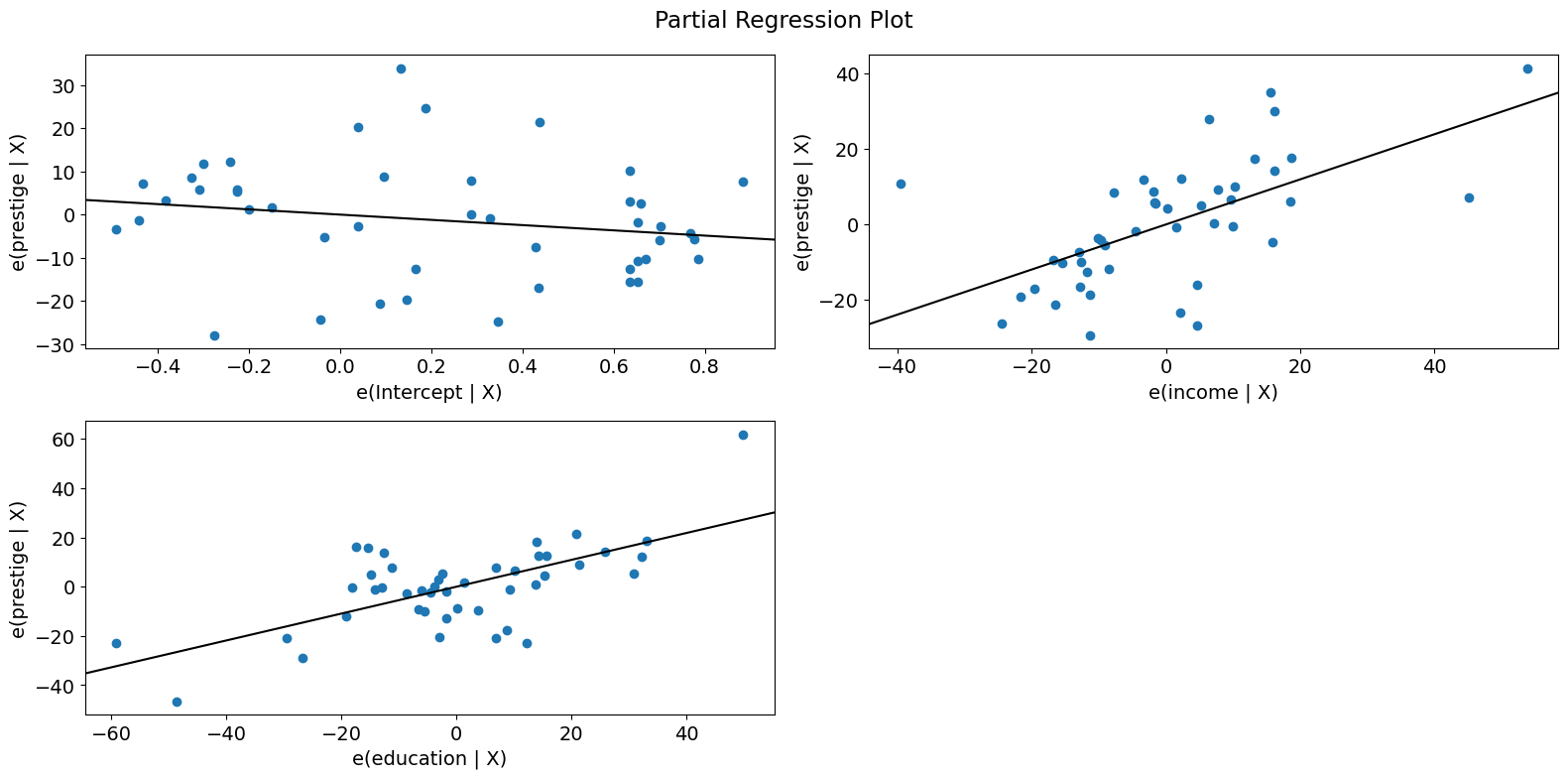
偏回归图 (邓肯)¶
由于我们正在进行多元回归,我们不能仅仅查看单个双变量图来辨别关系。相反,我们想要查看因变量与自变量在其他自变量条件下的关系。我们可以通过使用偏回归图来做到这一点,也称为添加变量图。
在偏回归图中,为了辨别响应变量与第 \(k\) 个变量的关系,我们通过回归响应变量与除 \(X_k\) 以外的自变量来计算残差。我们可以用 \(X_{\sim k}\) 表示它。然后,我们通过回归 \(X_k\) 与 \(X_{\sim k}\) 来计算残差。偏回归图是前者与后者残差的图。
该图值得注意的点是,拟合线的斜率为 \(\beta_k\),截距为零。该图的残差与完整 \(X\) 的原始模型的最小二乘拟合的残差相同。你可以很容易地辨别出各个数据值对系数估计的影响。如果 obs_labels 为 True,则这些点将用其观测值标签进行标注。你还可以看到对基本假设的违反,例如同方差性和线性性。
[8]:
fig = sm.graphics.plot_partregress(
"prestige", "income", ["income", "education"], data=prestige
)
fig.tight_layout(pad=1.0)
[9]:
fig = sm.graphics.plot_partregress("prestige", "income", ["education"], data=prestige)
fig.tight_layout(pad=1.0)
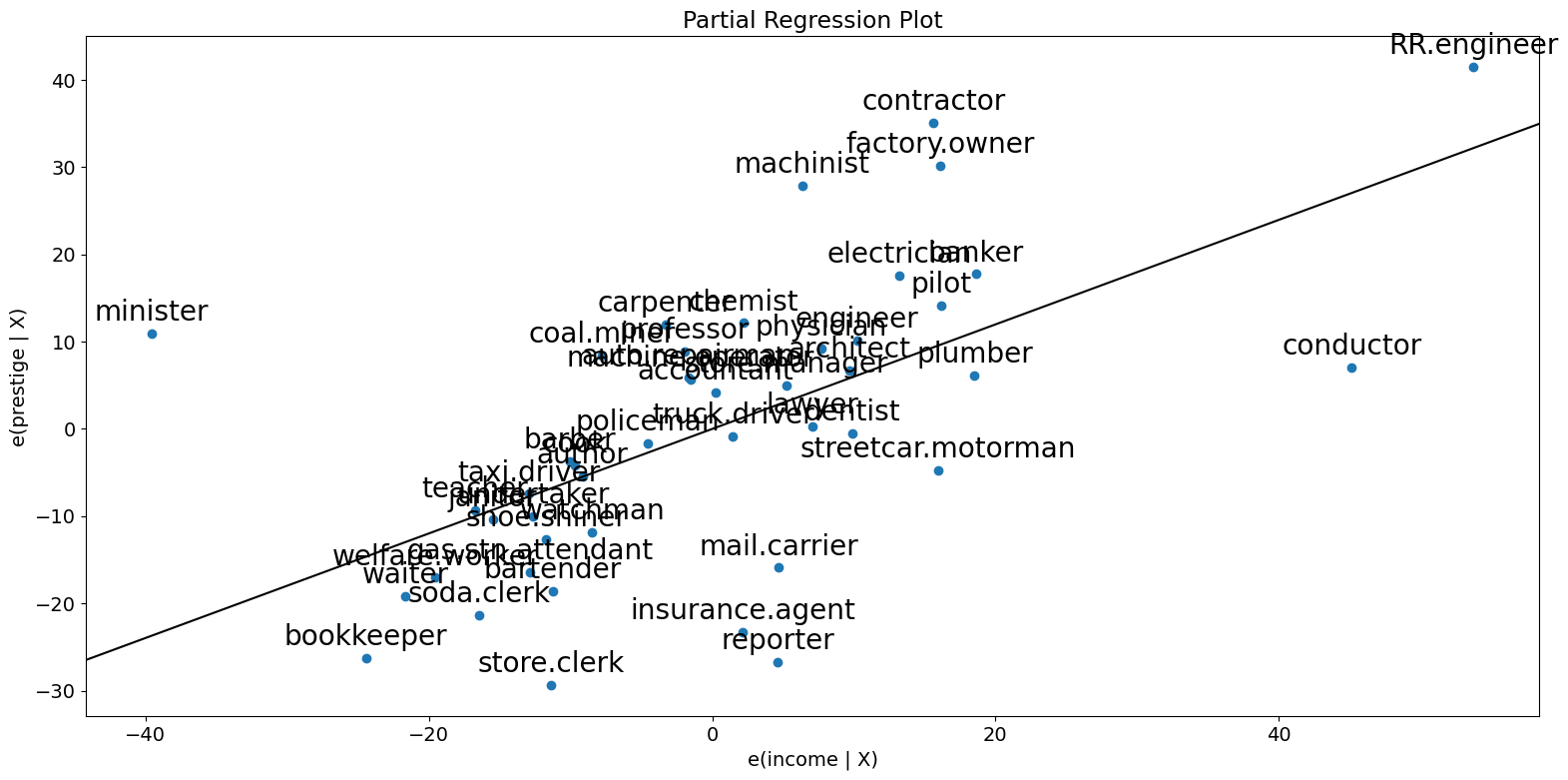
正如你所看到的,偏回归图证实了指挥家、牧师和 RR.engineer 对收入与声望之间偏关系的影响。这些案例大大降低了收入对声望的影响。删除这些案例证实了这一点。
[10]:
subset = ~prestige.index.isin(["conductor", "RR.engineer", "minister"])
prestige_model2 = ols(
"prestige ~ income + education", data=prestige, subset=subset
).fit()
print(prestige_model2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: prestige R-squared: 0.876
Model: OLS Adj. R-squared: 0.870
Method: Least Squares F-statistic: 138.1
Date: Thu, 03 Oct 2024 Prob (F-statistic): 2.02e-18
Time: 15:58:28 Log-Likelihood: -160.59
No. Observations: 42 AIC: 327.2
Df Residuals: 39 BIC: 332.4
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -6.3174 3.680 -1.717 0.094 -13.760 1.125
income 0.9307 0.154 6.053 0.000 0.620 1.242
education 0.2846 0.121 2.345 0.024 0.039 0.530
==============================================================================
Omnibus: 3.811 Durbin-Watson: 1.468
Prob(Omnibus): 0.149 Jarque-Bera (JB): 2.802
Skew: -0.614 Prob(JB): 0.246
Kurtosis: 3.303 Cond. No. 158.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
要快速检查所有回归变量,你可以使用 plot_partregress_grid。这些图不会标注点,但你可以使用它们来识别问题,然后使用 plot_partregress 获取更多信息。
[11]:
fig = sm.graphics.plot_partregress_grid(prestige_model)
fig.tight_layout(pad=1.0)
成分-成分加残差 (CCPR) 图¶
CCPR 图提供了一种方法来判断一个回归变量对响应变量的影响,方法是考虑其他自变量的影响。偏残差图定义为 \(\text{Residuals} + B_iX_i \text{ }\text{ }\) 对 \(X_i\) 的图。该成分添加了 \(B_iX_i\) 对 \(X_i\) 的图,以显示拟合线的位置。如果 \(X_i\) 与任何其他自变量高度相关,则应小心。如果是这种情况,图中明显的方差将是真实方差的低估。
[12]:
fig = sm.graphics.plot_ccpr(prestige_model, "education")
fig.tight_layout(pad=1.0)
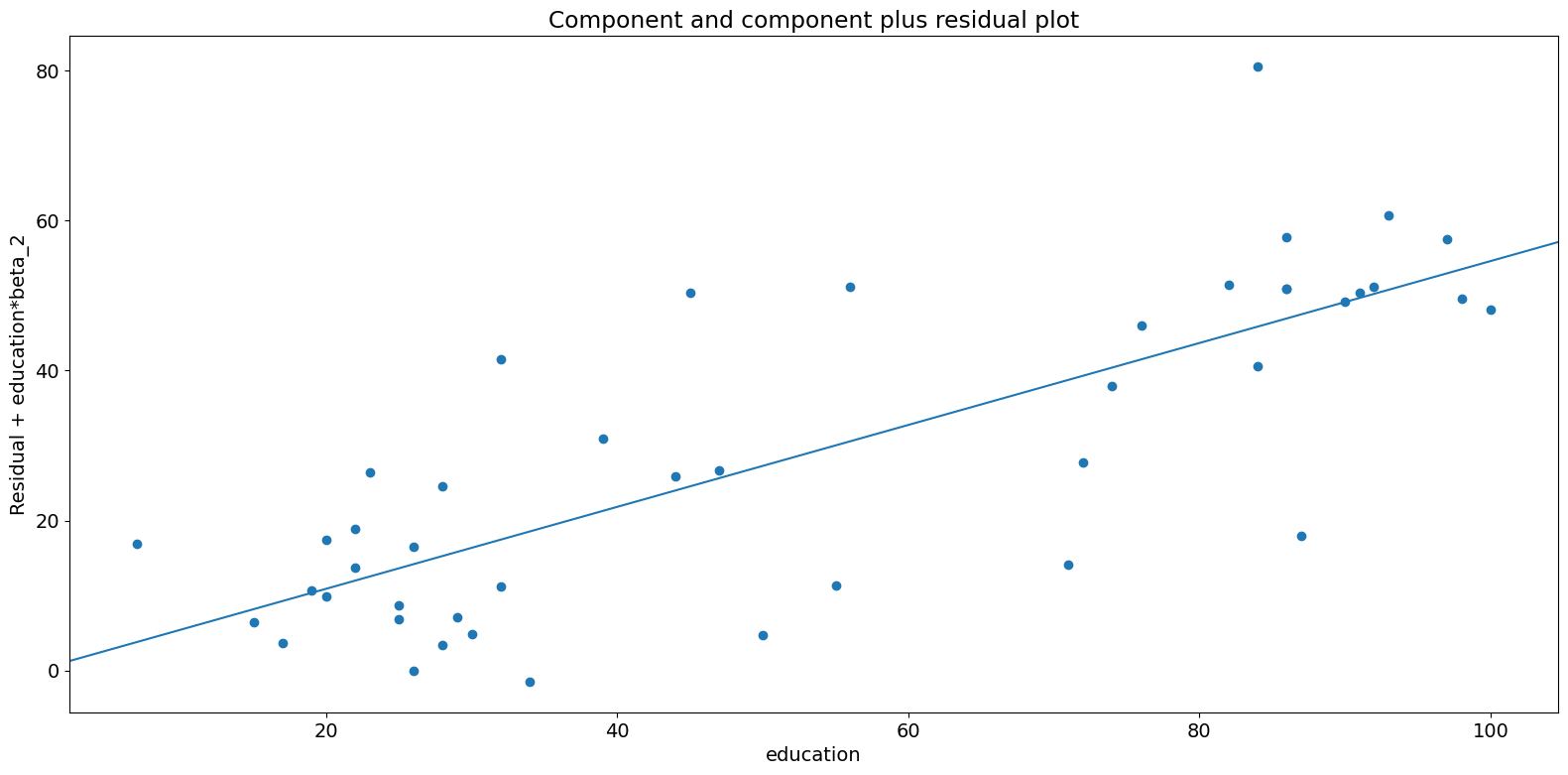
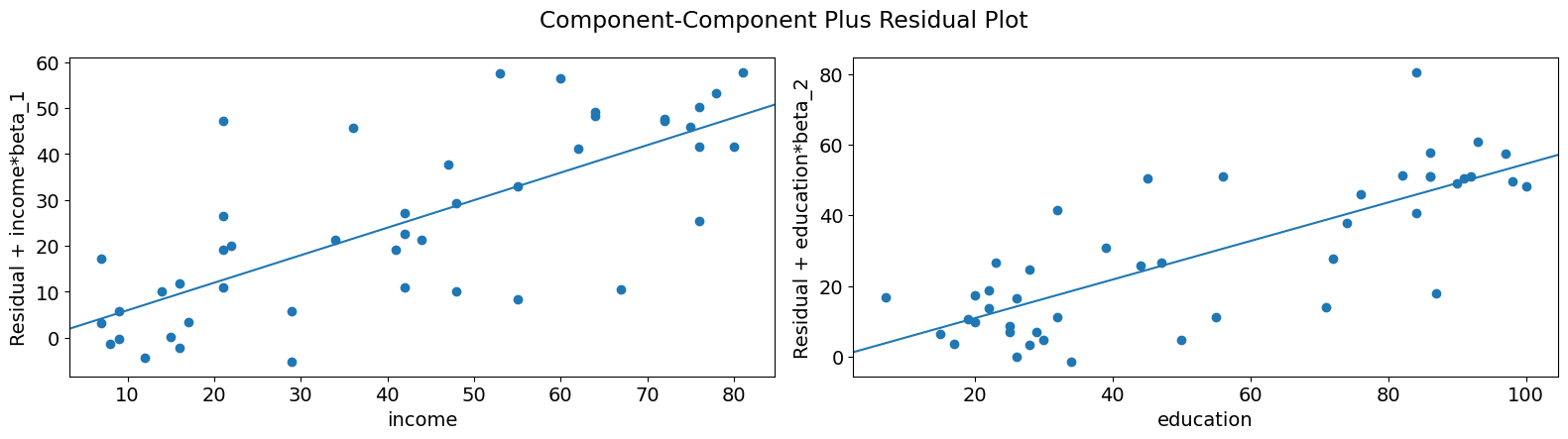
正如你所看到的,受教育程度解释的声望变化与收入条件下的关系似乎是线性的,尽管你可以看到有一些观测值对关系产生了相当大的影响。我们可以使用 plot_ccpr_grid 快速查看多个变量。
[13]:
fig = sm.graphics.plot_ccpr_grid(prestige_model)
fig.tight_layout(pad=1.0)
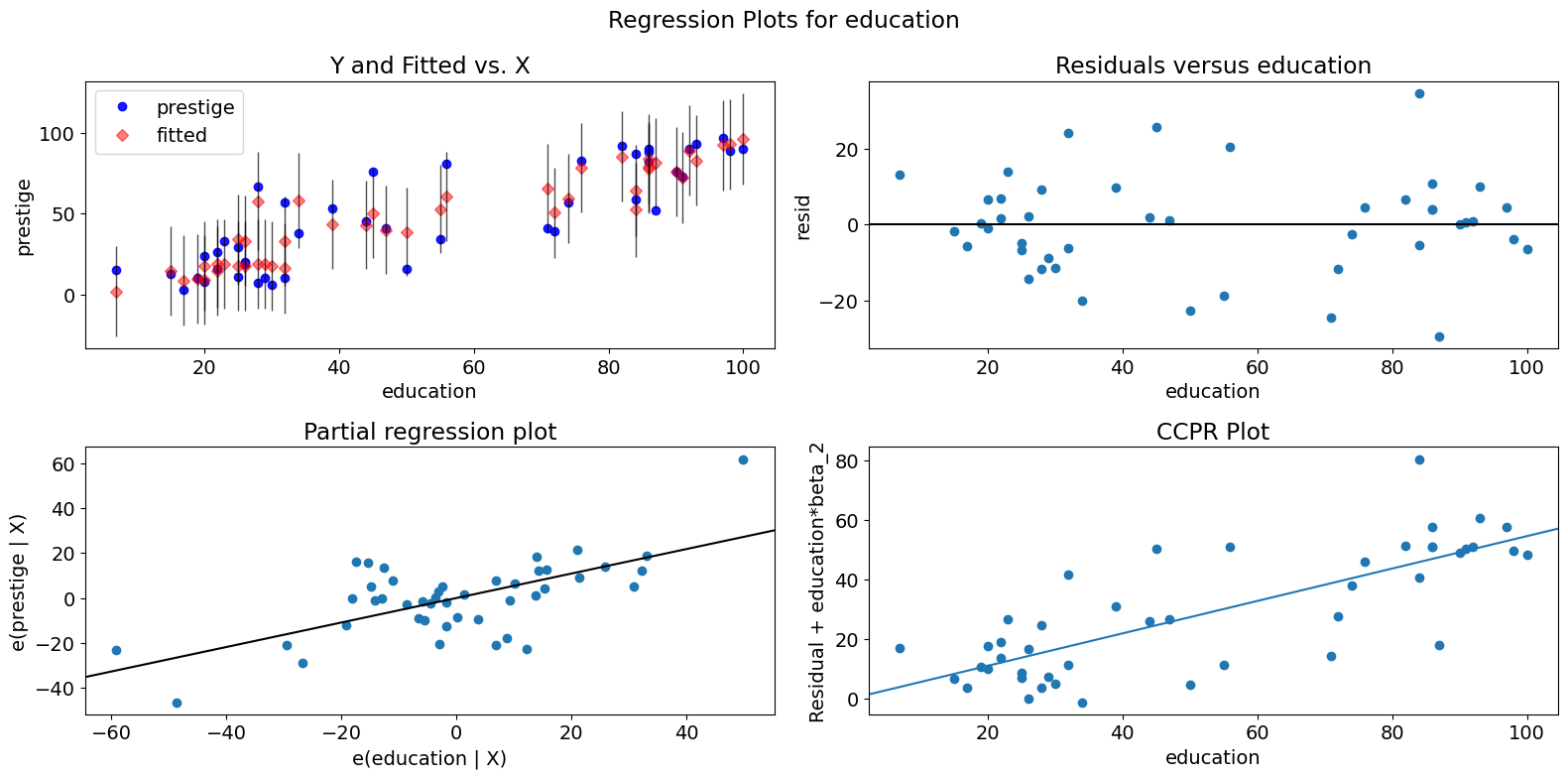
单变量回归诊断¶
plot_regress_exog 函数是一个方便的函数,它提供了一个 2x2 图,包含因变量和拟合值(带有置信区间)与所选自变量的关系,模型残差与所选自变量的关系,偏回归图以及 CCPR 图。该函数可用于快速检查模型对单个回归变量的假设。
[14]:
fig = sm.graphics.plot_regress_exog(prestige_model, "education")
fig.tight_layout(pad=1.0)
拟合图¶
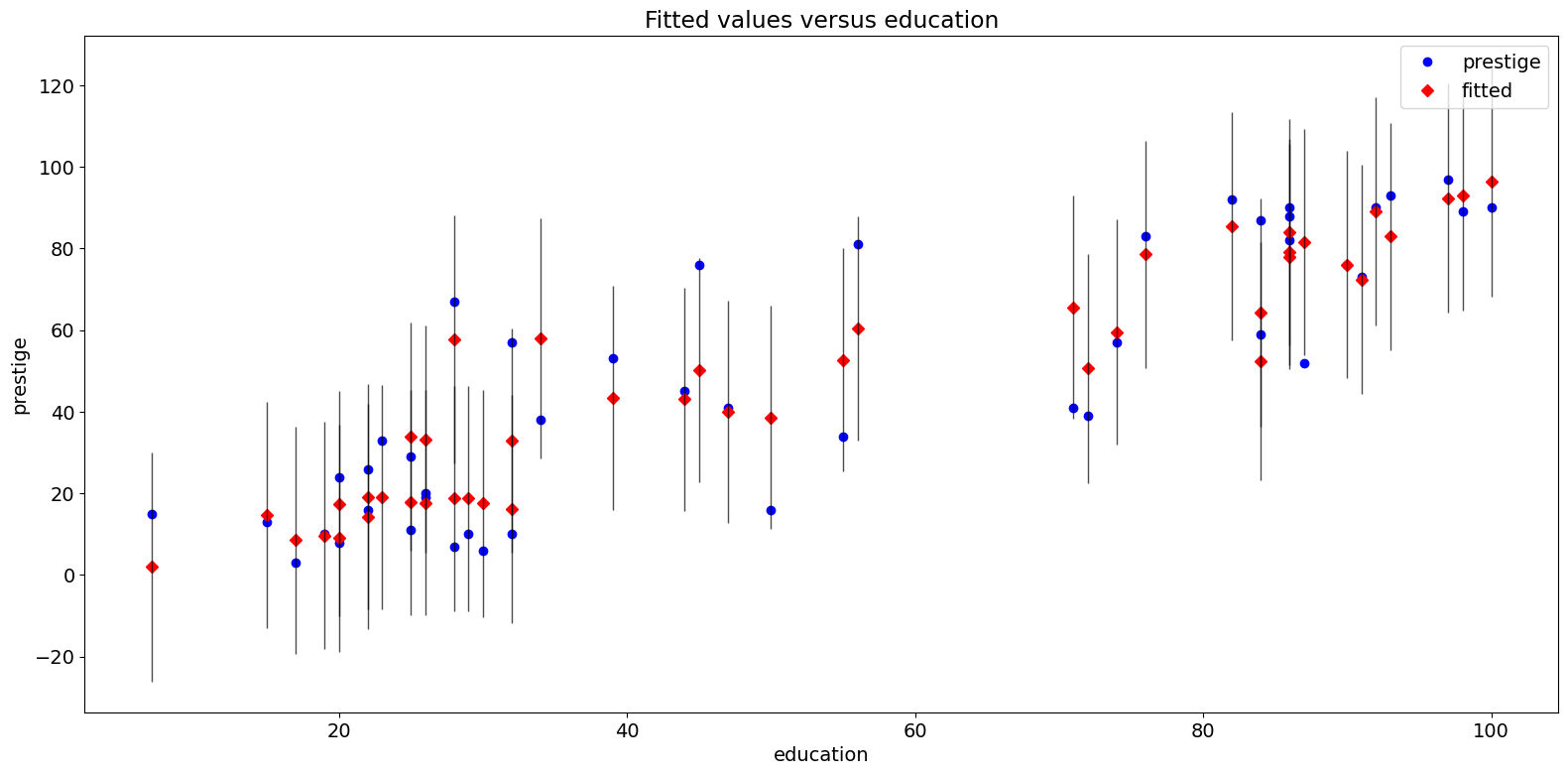
plot_fit 函数绘制拟合值与所选自变量的关系。它包括预测置信区间,并且可以选择绘制真实的因变量。
[15]:
fig = sm.graphics.plot_fit(prestige_model, "education")
fig.tight_layout(pad=1.0)
2009 年全州犯罪数据集¶
将以下内容与 http://www.ats.ucla.edu/stat/stata/webbooks/reg/chapter4/statareg_self_assessment_answers4.htm 进行比较
虽然这里的数据与该示例中的数据不同。你可以通过取消注释下面必要的单元格来运行该示例。
[16]:
# dta = pd.read_csv("http://www.stat.ufl.edu/~aa/social/csv_files/statewide-crime-2.csv")
# dta = dta.set_index("State", inplace=True).dropna()
# dta.rename(columns={"VR" : "crime",
# "MR" : "murder",
# "M" : "pctmetro",
# "W" : "pctwhite",
# "H" : "pcths",
# "P" : "poverty",
# "S" : "single"
# }, inplace=True)
#
# crime_model = ols("murder ~ pctmetro + poverty + pcths + single", data=dta).fit()
[17]:
dta = sm.datasets.statecrime.load_pandas().data
[18]:
crime_model = ols("murder ~ urban + poverty + hs_grad + single", data=dta).fit()
print(crime_model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: murder R-squared: 0.813
Model: OLS Adj. R-squared: 0.797
Method: Least Squares F-statistic: 50.08
Date: Thu, 03 Oct 2024 Prob (F-statistic): 3.42e-16
Time: 15:58:34 Log-Likelihood: -95.050
No. Observations: 51 AIC: 200.1
Df Residuals: 46 BIC: 209.8
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -44.1024 12.086 -3.649 0.001 -68.430 -19.774
urban 0.0109 0.015 0.707 0.483 -0.020 0.042
poverty 0.4121 0.140 2.939 0.005 0.130 0.694
hs_grad 0.3059 0.117 2.611 0.012 0.070 0.542
single 0.6374 0.070 9.065 0.000 0.496 0.779
==============================================================================
Omnibus: 1.618 Durbin-Watson: 2.507
Prob(Omnibus): 0.445 Jarque-Bera (JB): 0.831
Skew: -0.220 Prob(JB): 0.660
Kurtosis: 3.445 Cond. No. 5.80e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.8e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
偏回归图 (犯罪数据)¶
[19]:
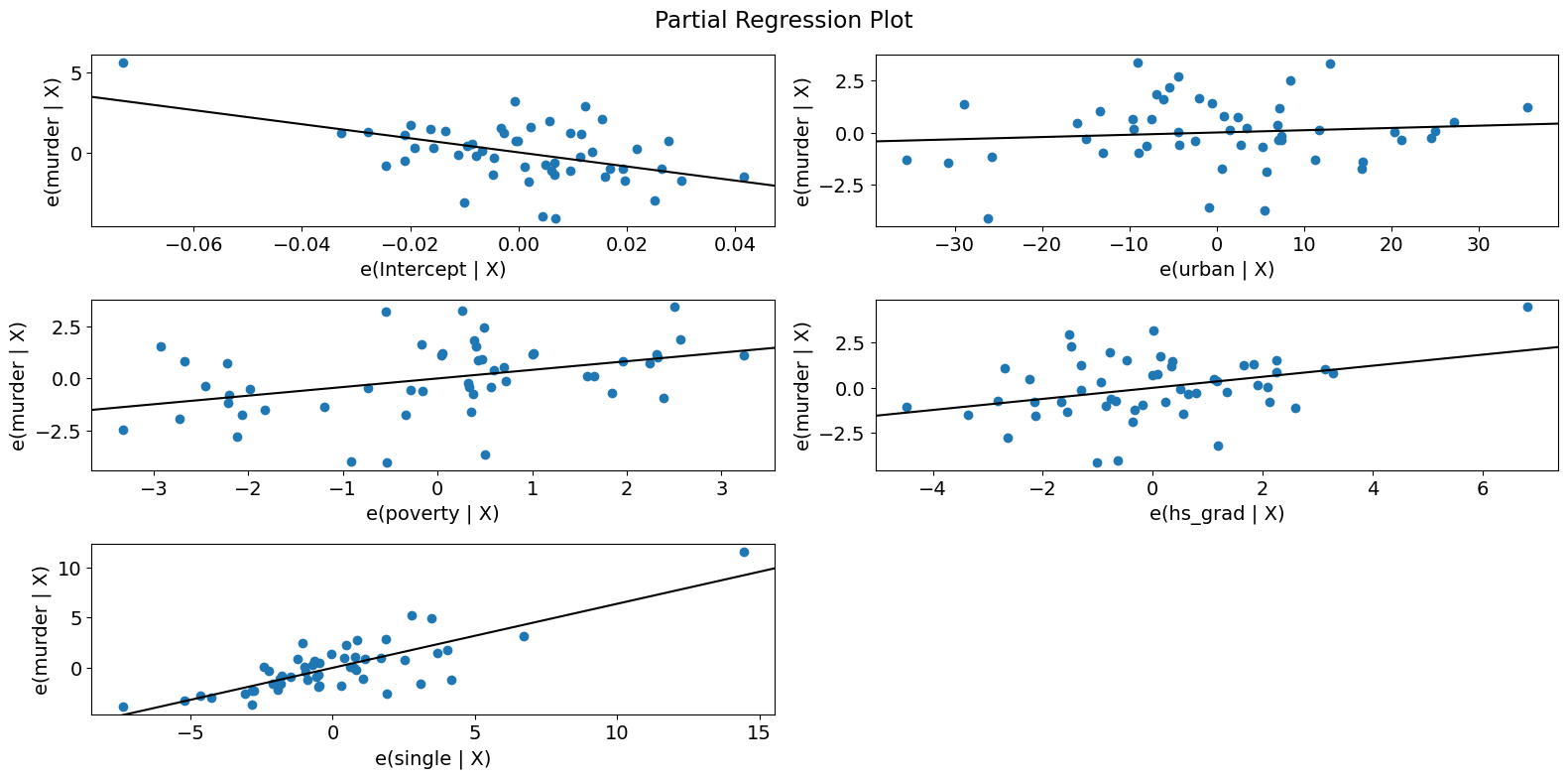
fig = sm.graphics.plot_partregress_grid(crime_model)
fig.tight_layout(pad=1.0)
[20]:
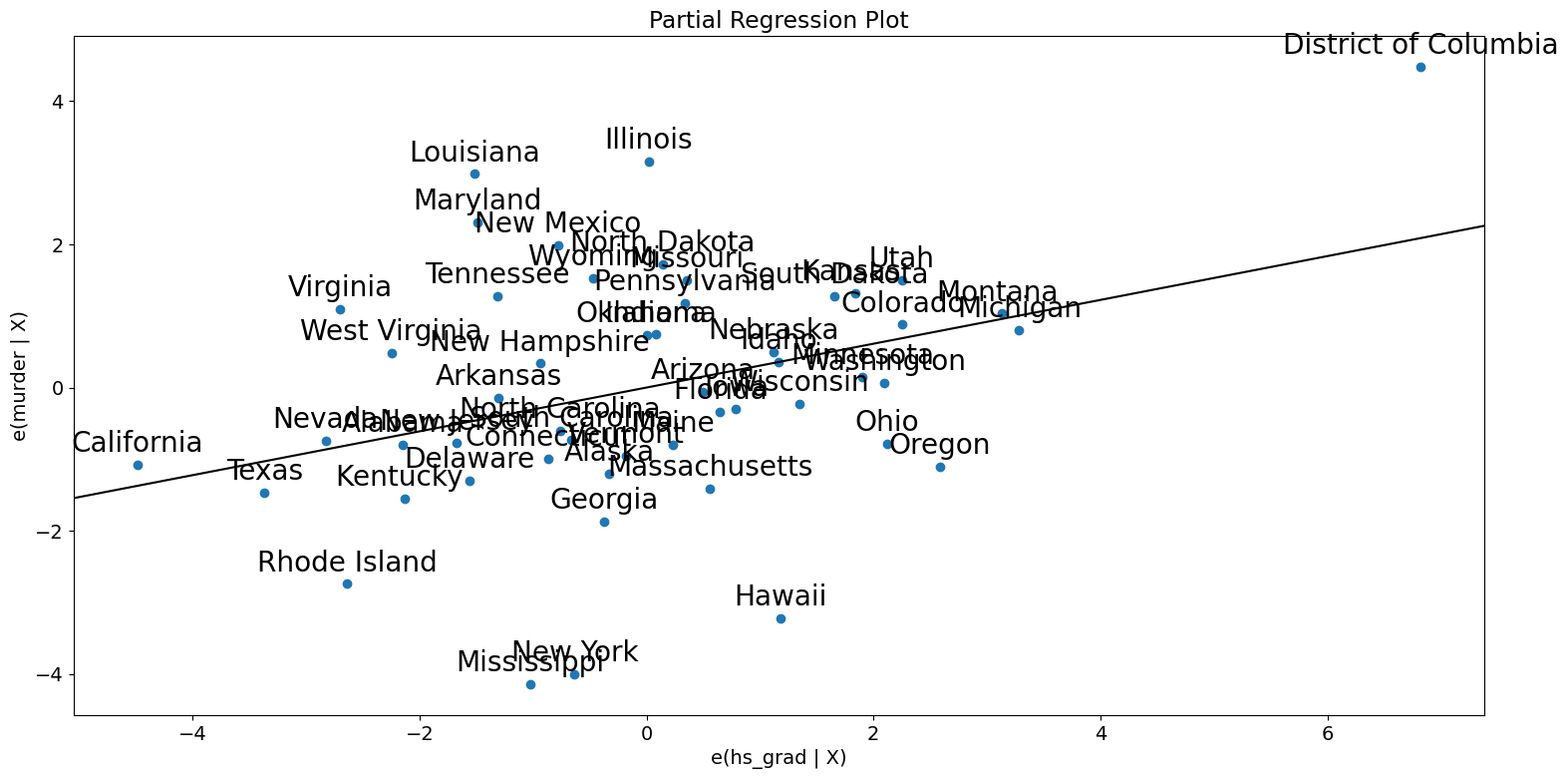
fig = sm.graphics.plot_partregress(
"murder", "hs_grad", ["urban", "poverty", "single"], data=dta
)
fig.tight_layout(pad=1.0)
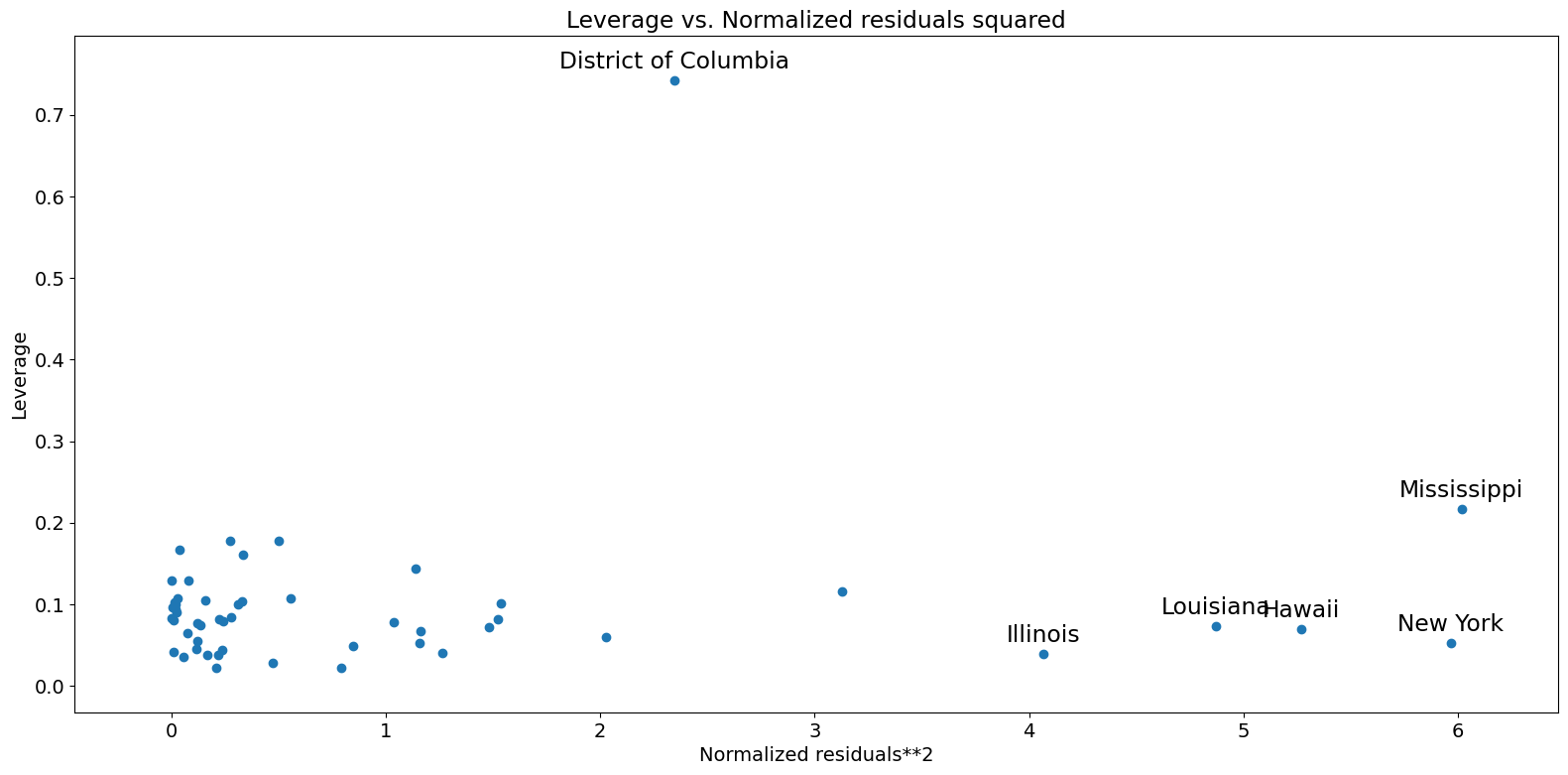
杠杆-残差平方图¶
与影响图密切相关的是杠杆-残差平方图。
[21]:
fig = sm.graphics.plot_leverage_resid2(crime_model)
fig.tight_layout(pad=1.0)
影响图¶
[22]:
fig = sm.graphics.influence_plot(crime_model)
fig.tight_layout(pad=1.0)
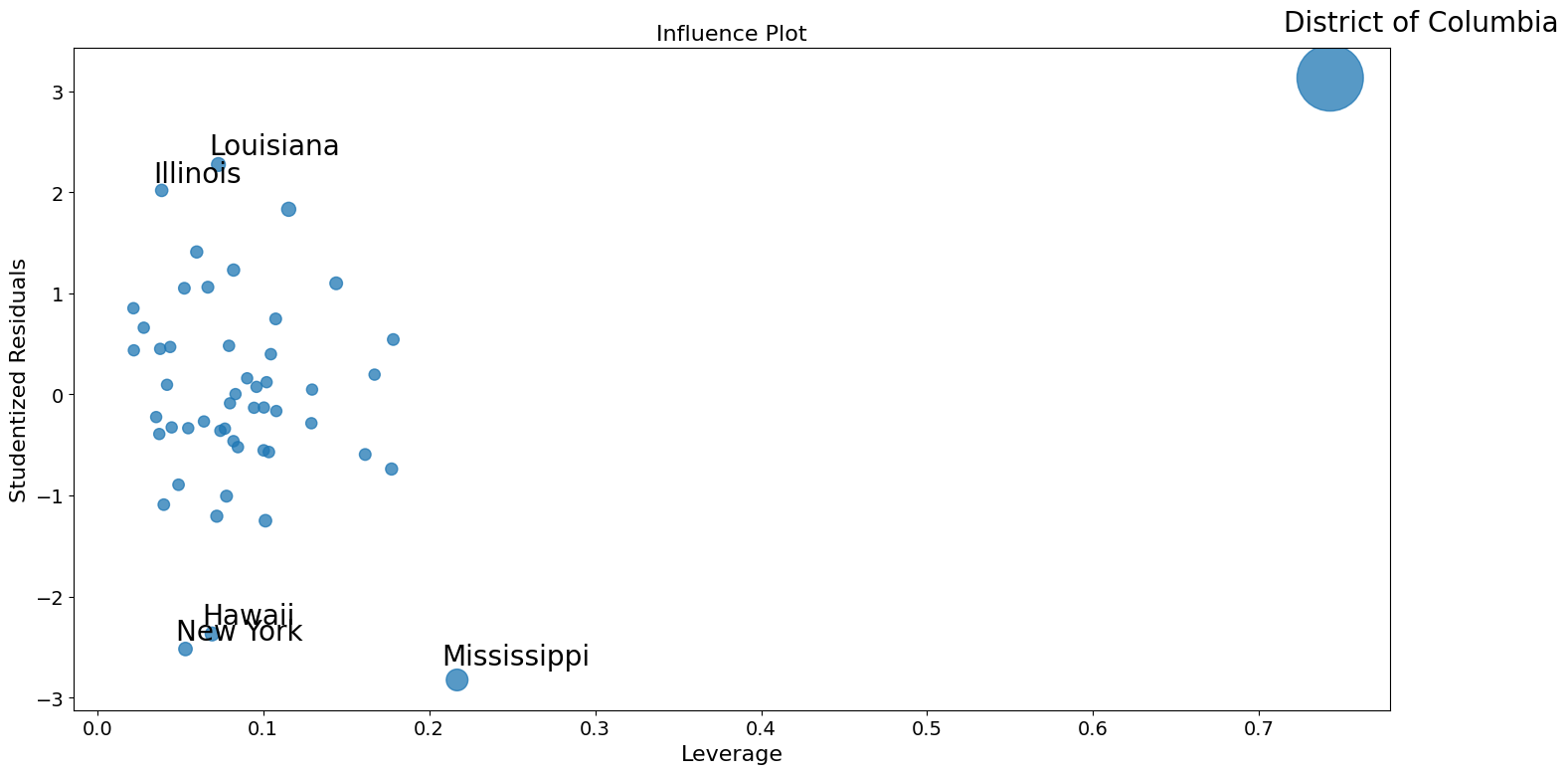
使用稳健回归来校正异常值。¶
这里重现 Stata 结果的一部分问题是,M 估计量对杠杆点不稳健。MM 估计量应该对这些示例更有效。
[23]:
from statsmodels.formula.api import rlm
[24]:
rob_crime_model = rlm(
"murder ~ urban + poverty + hs_grad + single",
data=dta,
M=sm.robust.norms.TukeyBiweight(3),
).fit(conv="weights")
print(rob_crime_model.summary())
Robust linear Model Regression Results
==============================================================================
Dep. Variable: murder No. Observations: 51
Model: RLM Df Residuals: 46
Method: IRLS Df Model: 4
Norm: TukeyBiweight
Scale Est.: mad
Cov Type: H1
Date: Thu, 03 Oct 2024
Time: 15:58:38
No. Iterations: 50
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -4.2986 9.494 -0.453 0.651 -22.907 14.310
urban 0.0029 0.012 0.241 0.809 -0.021 0.027
poverty 0.2753 0.110 2.499 0.012 0.059 0.491
hs_grad -0.0302 0.092 -0.328 0.743 -0.211 0.150
single 0.2902 0.055 5.253 0.000 0.182 0.398
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
[25]:
# rob_crime_model = rlm("murder ~ pctmetro + poverty + pcths + single", data=dta, M=sm.robust.norms.TukeyBiweight()).fit(conv="weights")
# print(rob_crime_model.summary())
RLM 中还没有影响诊断方法,但我们可以重新创建它们。(这取决于 issue #888 的状态)
[26]:
weights = rob_crime_model.weights
idx = weights > 0
X = rob_crime_model.model.exog[idx.values]
ww = weights[idx] / weights[idx].mean()
hat_matrix_diag = ww * (X * np.linalg.pinv(X).T).sum(1)
resid = rob_crime_model.resid
resid2 = resid ** 2
resid2 /= resid2.sum()
nobs = int(idx.sum())
hm = hat_matrix_diag.mean()
rm = resid2.mean()
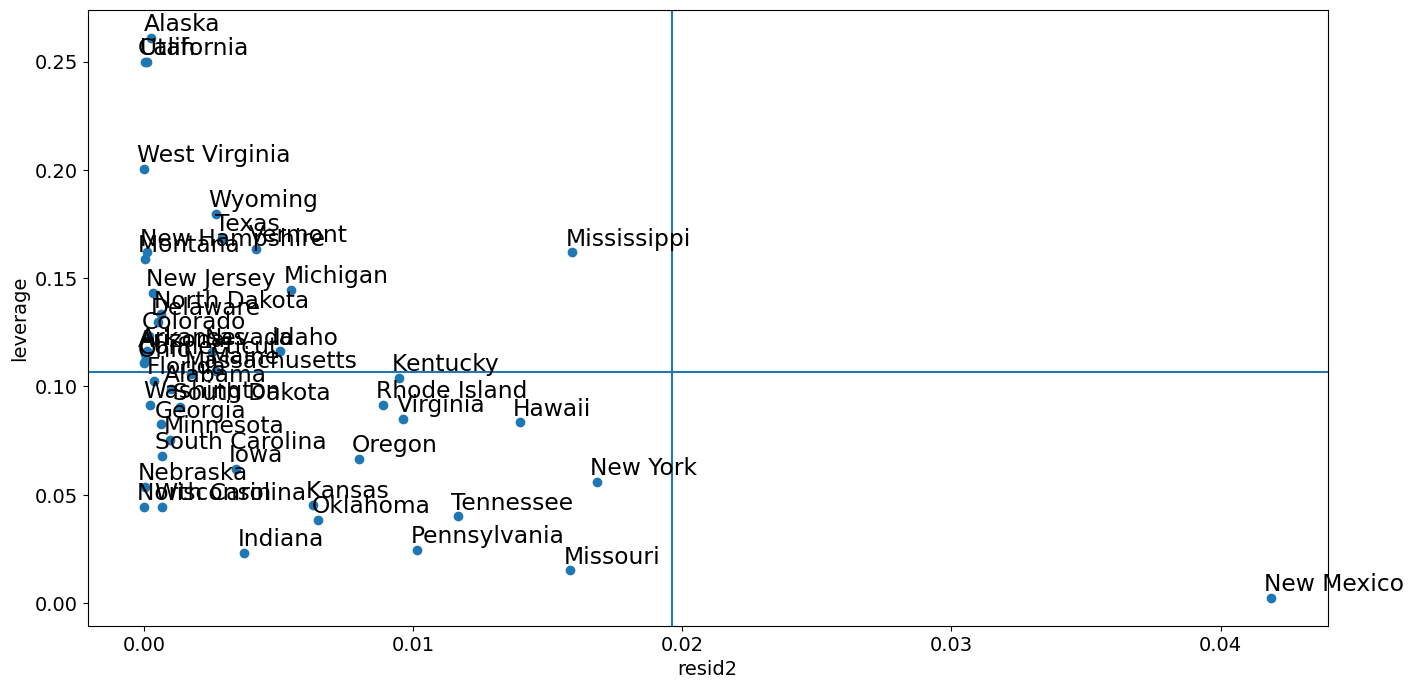
[27]:
from statsmodels.graphics import utils
fig, ax = plt.subplots(figsize=(16, 8))
ax.plot(resid2[idx], hat_matrix_diag, "o")
ax = utils.annotate_axes(
range(nobs),
labels=rob_crime_model.model.data.row_labels[idx],
points=lzip(resid2[idx], hat_matrix_diag),
offset_points=[(-5, 5)] * nobs,
size="large",
ax=ax,
)
ax.set_xlabel("resid2")
ax.set_ylabel("leverage")
ylim = ax.get_ylim()
ax.vlines(rm, *ylim)
xlim = ax.get_xlim()
ax.hlines(hm, *xlim)
ax.margins(0, 0)