线性混合效应模型¶
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.tools.sm_exceptions import ConvergenceWarning
**注意:** 此笔记本中的 R 代码和结果已转换为 markdown,因此构建文档不需要 R。 笔记本中的 R 结果是使用 R 3.5.1 和 lme4 1.1 计算的。
%load_ext rpy2.ipython
%R library(lme4)
array(['lme4', 'Matrix', 'tools', 'stats', 'graphics', 'grDevices',
'utils', 'datasets', 'methods', 'base'], dtype='<U9')
比较 R lmer 和 statsmodels MixedLM¶
statsmodels 中的线性混合模型 (MixedLM) 实现紧密遵循 Lindstrom 和 Bates (JASA 1988) 中概述的方法。 这也是 R 包 LME4 中采用的方法。 Stata、SAS 等其他软件包也应该与此方法一致,因为该领域的 基本技术大部分已经成熟。
这里我们展示了如何使用 statsmodels 中的 MixedLM 过程拟合线性混合模型。 包含来自 R (LME4) 的结果以进行比较。
以下是我们的导入语句
猪的生长曲线¶
这些是来自析因实验的纵向数据。 结果变量是每只猪的体重,此处我们将使用的唯一预测变量是“时间”。 首先,我们拟合一个模型,该模型将平均体重表示为时间的线性函数,每只猪的截距都不同。 模型是使用公式指定的。 由于没有指定随机效应结构,因此自动使用默认随机效应结构(每个组的随机截距)。
[2]:
data = sm.datasets.get_rdataset("dietox", "geepack").data
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"])
mdf = md.fit(method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 11.3669
Min. group size: 11 Log-Likelihood: -2404.7753
Max. group size: 12 Converged: Yes
Mean group size: 12.0
--------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
--------------------------------------------------------
Intercept 15.724 0.788 19.952 0.000 14.179 17.268
Time 6.943 0.033 207.939 0.000 6.877 7.008
Group Var 40.395 2.149
========================================================
以下是使用 LMER 在 R 中拟合的相同模型
%%R
data(dietox, package='geepack')
%R print(summary(lmer('Weight ~ Time + (1|Pig)', data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 | Pig)
Data: dietox
REML criterion at convergence: 4809.6
Scaled residuals:
Min 1Q Median 3Q Max
-4.7118 -0.5696 -0.0943 0.4877 4.7732
Random effects:
Groups Name Variance Std.Dev.
Pig (Intercept) 40.39 6.356
Residual 11.37 3.371
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.72352 0.78805 19.95
Time 6.94251 0.03339 207.94
Correlation of Fixed Effects:
(Intr)
Time -0.275
请注意,在 statsmodels 结果摘要中,固定效应和随机效应参数估计值显示在单个表中。 上面的 statsmodels 输出中,动物的随机效应标记为“Intercept RE”。 在 LME4 输出中,此效应是随机效应部分下的猪截距。
关于随机效应方差和协方差参数的标准误差是否有用,一直存在很多争议。 在 LME4 中,这些标准误差没有显示,因为该软件包的作者认为它们信息量不大。 虽然有充分的理由质疑它们的效用,但我们选择在摘要表中包含标准误差,但不会显示相应的 Wald 置信区间。
接下来,我们拟合了一个模型,每个动物有两个随机效应:随机截距和随机斜率(相对于时间)。 这意味着每只猪可能具有不同的基线体重,并且生长速度也不同。 该公式指定“时间”是一个具有随机系数的协变量。 默认情况下,公式始终包含一个截距(可以使用“0 + 时间”作为公式在此处进行抑制)。
[3]:
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time")
mdf = md.fit(method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
===========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 6.0372
Min. group size: 11 Log-Likelihood: -2217.0475
Max. group size: 12 Converged: Yes
Mean group size: 12.0
-----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------
Intercept 15.739 0.550 28.603 0.000 14.660 16.817
Time 6.939 0.080 86.925 0.000 6.783 7.095
Group Var 19.503 1.561
Group x Time Cov 0.294 0.153
Time Var 0.416 0.033
===========================================================
以下是使用 LMER 在 R 中拟合的相同模型
%R print(summary(lmer("Weight ~ Time + (1 + Time | Pig)", data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 + Time | Pig)
Data: dietox
REML criterion at convergence: 4434.1
Scaled residuals:
Min 1Q Median 3Q Max
-6.4286 -0.5529 -0.0416 0.4841 3.5624
Random effects:
Groups Name Variance Std.Dev. Corr
Pig (Intercept) 19.493 4.415
Time 0.416 0.645 0.10
Residual 6.038 2.457
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.73865 0.55012 28.61
Time 6.93901 0.07982 86.93
Correlation of Fixed Effects:
(Intr)
Time 0.006
随机截距和随机斜率仅弱相关 \((0.294 / \sqrt{19.493 * 0.416} \approx 0.1)\)。 因此,接下来我们将拟合一个模型,其中两个随机效应被限制为不相关
[4]:
0.294 / (19.493 * 0.416) ** 0.5
[4]:
0.10324316832591753
[5]:
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time")
free = sm.regression.mixed_linear_model.MixedLMParams.from_components(
np.ones(2), np.eye(2)
)
mdf = md.fit(free=free, method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
===========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 6.0283
Min. group size: 11 Log-Likelihood: -2217.3481
Max. group size: 12 Converged: Yes
Mean group size: 12.0
-----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------
Intercept 15.739 0.554 28.388 0.000 14.652 16.825
Time 6.939 0.080 86.248 0.000 6.781 7.097
Group Var 19.837 1.571
Group x Time Cov 0.000 0.000
Time Var 0.423 0.033
===========================================================
当我们将相关参数固定为 0 时,似然性下降了 0.3。 将 2 x 0.3 = 0.6 与 chi^2 1 df 参考分布进行比较表明,数据与该参数等于 0 的模型非常一致。
以下是使用 LMER 在 R 中拟合的相同模型(请注意,此处 R 报告的是 REML 准则而不是似然性,其中 REML 准则是对数似然的两倍)
%R print(summary(lmer("Weight ~ Time + (1 | Pig) + (0 + Time | Pig)", data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 | Pig) + (0 + Time | Pig)
Data: dietox
REML criterion at convergence: 4434.7
Scaled residuals:
Min 1Q Median 3Q Max
-6.4281 -0.5527 -0.0405 0.4840 3.5661
Random effects:
Groups Name Variance Std.Dev.
Pig (Intercept) 19.8404 4.4543
Pig.1 Time 0.4234 0.6507
Residual 6.0282 2.4552
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.73875 0.55444 28.39
Time 6.93899 0.08045 86.25
Correlation of Fixed Effects:
(Intr)
Time -0.086
西卡生长数据¶
这是 LMER R 库中提供的示例数据集之一。 结果变量是树木的大小,此处使用的协变量是时间值。 数据按树进行分组。
[6]:
data = sm.datasets.get_rdataset("Sitka", "MASS").data
endog = data["size"]
data["Intercept"] = 1
exog = data[["Intercept", "Time"]]
以下是使用 statsmodels LME 对具有随机截距的基本模型进行拟合。 我们将 endog 和 exog 数据作为数组直接传递给 LME 初始化函数。 另请注意,endog_re 在参数 4 中被明确指定为随机截距(尽管如果未指定,这也是默认值)。
[7]:
md = sm.MixedLM(endog, exog, groups=data["tree"], exog_re=exog["Intercept"])
mdf = md.fit()
print(mdf.summary())
Mixed Linear Model Regression Results
=======================================================
Model: MixedLM Dependent Variable: size
No. Observations: 395 Method: REML
No. Groups: 79 Scale: 0.0392
Min. group size: 5 Log-Likelihood: -82.3884
Max. group size: 5 Converged: Yes
Mean group size: 5.0
-------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-------------------------------------------------------
Intercept 2.273 0.088 25.864 0.000 2.101 2.446
Time 0.013 0.000 47.796 0.000 0.012 0.013
Intercept Var 0.374 0.345
=======================================================
以下是使用 LMER 在 R 中拟合的相同模型
%R
data(Sitka, package="MASS")
print(summary(lmer("size ~ Time + (1 | tree)", data=Sitka)))
Linear mixed model fit by REML ['lmerMod']
Formula: size ~ Time + (1 | tree)
Data: Sitka
REML criterion at convergence: 164.8
Scaled residuals:
Min 1Q Median 3Q Max
-2.9979 -0.5169 0.1576 0.5392 4.4012
Random effects:
Groups Name Variance Std.Dev.
tree (Intercept) 0.37451 0.612
Residual 0.03921 0.198
Number of obs: 395, groups: tree, 79
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.2732443 0.0878955 25.86
Time 0.0126855 0.0002654 47.80
Correlation of Fixed Effects:
(Intr)
Time -0.611
现在我们可以尝试添加随机斜率。 我们先从 R 开始。 从下面的代码和输出中,我们可以看到随机斜率方差的 REML 估计值几乎为零。
%R print(summary(lmer("size ~ Time + (1 + Time | tree)", data=Sitka)))
Linear mixed model fit by REML ['lmerMod']
Formula: size ~ Time + (1 + Time | tree)
Data: Sitka
REML criterion at convergence: 153.4
Scaled residuals:
Min 1Q Median 3Q Max
-2.7609 -0.5173 0.1188 0.5270 3.5466
Random effects:
Groups Name Variance Std.Dev. Corr
tree (Intercept) 2.217e-01 0.470842
Time 3.288e-06 0.001813 -0.17
Residual 3.634e-02 0.190642
Number of obs: 395, groups: tree, 79
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.273244 0.074655 30.45
Time 0.012686 0.000327 38.80
Correlation of Fixed Effects:
(Intr)
Time -0.615
convergence code: 0
Model failed to converge with max|grad| = 0.793203 (tol = 0.002, component 1)
Model is nearly unidentifiable: very large eigenvalue
- Rescale variables?
如果我们在 statsmodels LME 中使用默认值运行此命令,我们会看到方差估计确实非常小,这会导致关于解位于参数空间边界上的警告。 回归斜率与 R 的斜率非常吻合,但似然性值远高于 R 返回的值。
[8]:
exog_re = exog.copy()
md = sm.MixedLM(endog, exog, data["tree"], exog_re)
mdf = md.fit()
print(mdf.summary())
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/regression/mixed_linear_model.py:2237: ConvergenceWarning: The MLE may be on the boundary of the parameter space.
warnings.warn(msg, ConvergenceWarning)
Mixed Linear Model Regression Results
===============================================================
Model: MixedLM Dependent Variable: size
No. Observations: 395 Method: REML
No. Groups: 79 Scale: 0.0264
Min. group size: 5 Log-Likelihood: -62.4834
Max. group size: 5 Converged: Yes
Mean group size: 5.0
---------------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
---------------------------------------------------------------
Intercept 2.273 0.101 22.513 0.000 2.075 2.471
Time 0.013 0.000 33.888 0.000 0.012 0.013
Intercept Var 0.646 0.914
Intercept x Time Cov -0.001 0.003
Time Var 0.000 0.000
===============================================================
我们可以通过构建配置文件似然性的图形来进一步探索随机效应结构。 我们从随机截距开始,生成一个从 MLE 以下 0.1 个单位到以上 0.1 个单位的配置文件似然性图。 由于配置文件似然性内的每次优化都会产生警告(由于随机斜率方差接近于零),因此我们在此处关闭警告。
[9]:
import warnings
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
likev = mdf.profile_re(0, "re", dist_low=0.1, dist_high=0.1)
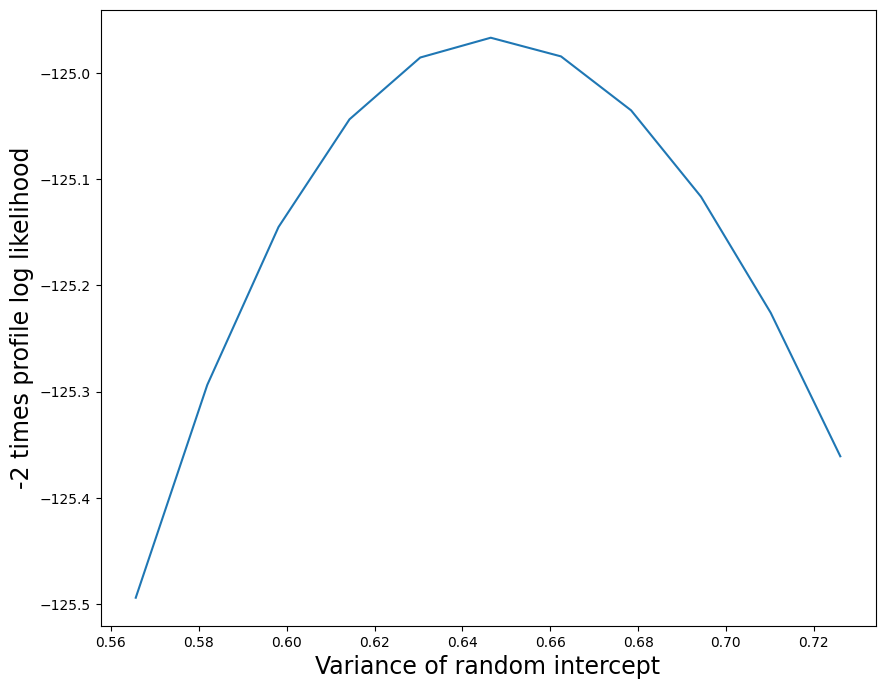
以下是配置文件似然性函数的图形。 我们将对数似然性差值乘以 2 以获得具有 1 个自由度的常用 \(\chi^2\) 参考分布。
[10]:
import matplotlib.pyplot as plt
[11]:
plt.figure(figsize=(10, 8))
plt.plot(likev[:, 0], 2 * likev[:, 1])
plt.xlabel("Variance of random intercept", size=17)
plt.ylabel("-2 times profile log likelihood", size=17)
[11]:
Text(0, 0.5, '-2 times profile log likelihood')
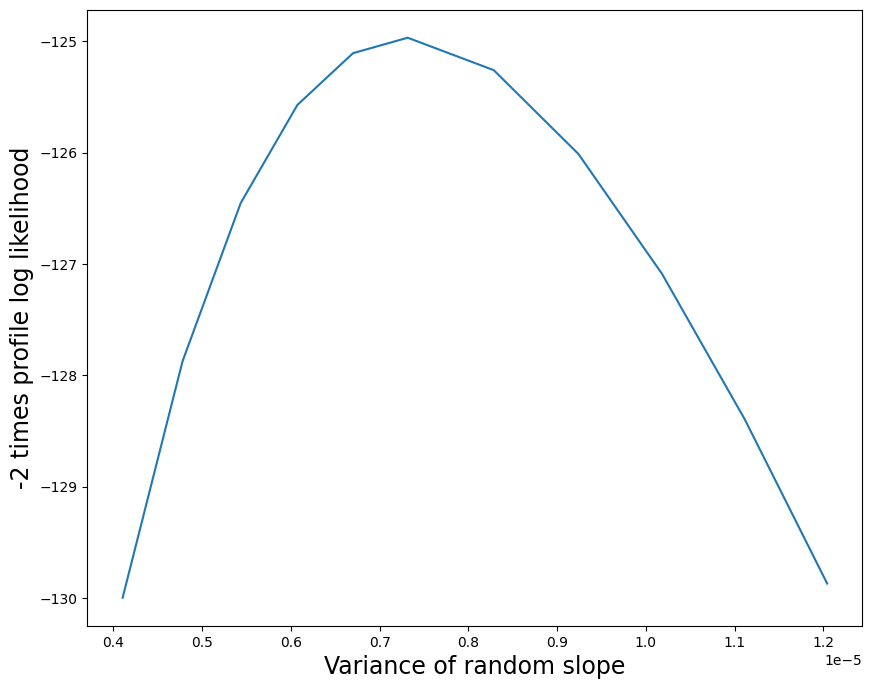
以下是配置文件似然性函数的图形。 配置文件似然性图显示,随机斜率方差参数的 MLE 是一个非常小的正数,并且此估计值的不确定性很低。
[12]:
re = mdf.cov_re.iloc[1, 1]
with warnings.catch_warnings():
# Parameter is often on the boundary
warnings.simplefilter("ignore", ConvergenceWarning)
likev = mdf.profile_re(1, "re", dist_low=0.5 * re, dist_high=0.8 * re)
plt.figure(figsize=(10, 8))
plt.plot(likev[:, 0], 2 * likev[:, 1])
plt.xlabel("Variance of random slope", size=17)
lbl = plt.ylabel("-2 times profile log likelihood", size=17)