分位数回归¶
本示例页面展示了如何使用 statsmodels 的 QuantReg 类来复制发表在
Koenker, Roger 和 Kevin F. Hallock。 “分位数回归”。《经济学视角杂志》,第 15 卷,第 4 期,2001 年秋季,第 143-156 页
我们感兴趣的是 1857 年比利时工作阶层家庭样本中收入与食品支出之间的关系(恩格尔数据)。
设置¶
首先,我们需要加载一些模块并检索数据。方便的是,恩格尔数据集与 statsmodels 一起提供。
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
data = sm.datasets.engel.load_pandas().data
data.head()
[2]:
| 收入 | 食品支出 | |
|---|---|---|
| 0 | 420.157651 | 255.839425 |
| 1 | 541.411707 | 310.958667 |
| 2 | 901.157457 | 485.680014 |
| 3 | 639.080229 | 402.997356 |
| 4 | 750.875606 | 495.560775 |
最小绝对偏差¶
LAD 模型是分位数回归的特殊情况,其中 q=0.5
[3]:
mod = smf.quantreg("foodexp ~ income", data)
res = mod.fit(q=0.5)
print(res.summary())
QuantReg Regression Results
==============================================================================
Dep. Variable: foodexp Pseudo R-squared: 0.6206
Model: QuantReg Bandwidth: 64.51
Method: Least Squares Sparsity: 209.3
Date: Thu, 03 Oct 2024 No. Observations: 235
Time: 15:46:19 Df Residuals: 233
Df Model: 1
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 81.4823 14.634 5.568 0.000 52.649 110.315
income 0.5602 0.013 42.516 0.000 0.534 0.586
==============================================================================
The condition number is large, 2.38e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
可视化结果¶
我们为 .05 到 .95 之间的许多分位数估计分位数回归模型,并将这些模型中最佳拟合线与普通最小二乘结果进行比较。
准备绘图数据¶
为了方便起见,我们将分位数回归结果放在 Pandas DataFrame 中,并将 OLS 结果放在字典中。
[4]:
quantiles = np.arange(0.05, 0.96, 0.1)
def fit_model(q):
res = mod.fit(q=q)
return [q, res.params["Intercept"], res.params["income"]] + res.conf_int().loc[
"income"
].tolist()
models = [fit_model(x) for x in quantiles]
models = pd.DataFrame(models, columns=["q", "a", "b", "lb", "ub"])
ols = smf.ols("foodexp ~ income", data).fit()
ols_ci = ols.conf_int().loc["income"].tolist()
ols = dict(
a=ols.params["Intercept"], b=ols.params["income"], lb=ols_ci[0], ub=ols_ci[1]
)
print(models)
print(ols)
q a b lb ub
0 0.05 124.880096 0.343361 0.268632 0.418090
1 0.15 111.693660 0.423708 0.382780 0.464636
2 0.25 95.483539 0.474103 0.439900 0.508306
3 0.35 105.841294 0.488901 0.457759 0.520043
4 0.45 81.083647 0.552428 0.525021 0.579835
5 0.55 89.661370 0.565601 0.540955 0.590247
6 0.65 74.033434 0.604576 0.582169 0.626982
7 0.75 62.396584 0.644014 0.622411 0.665617
8 0.85 52.272216 0.677603 0.657383 0.697823
9 0.95 64.103964 0.709069 0.687831 0.730306
{'a': np.float64(147.47538852370573), 'b': np.float64(0.48517842367692354), 'lb': 0.4568738130184233, 'ub': 0.5134830343354237}
第一个图¶
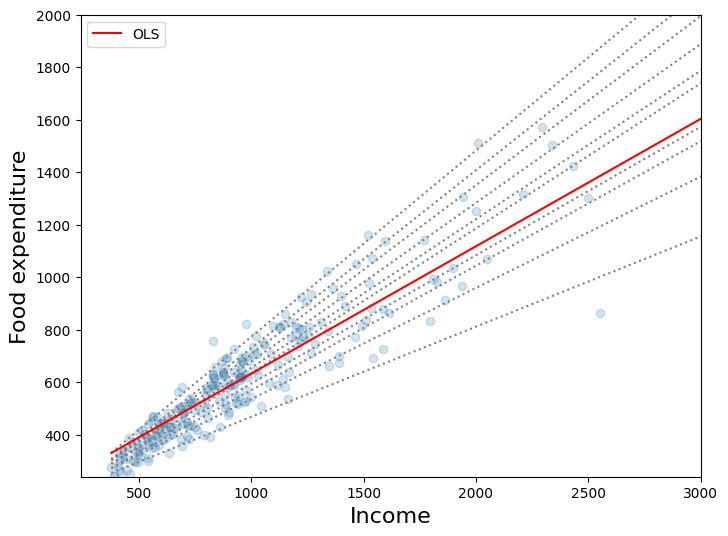
该图将 10 个分位数回归模型的最佳拟合线与最小二乘拟合进行了比较。正如 Koenker 和 Hallock(2001)指出的那样,我们看到
食品支出随收入增加
食品支出的离散度随收入增加
最小二乘估计对低收入观测值拟合得不太好(即 OLS 线经过大多数低收入家庭)
[5]:
x = np.arange(data.income.min(), data.income.max(), 50)
get_y = lambda a, b: a + b * x
fig, ax = plt.subplots(figsize=(8, 6))
for i in range(models.shape[0]):
y = get_y(models.a[i], models.b[i])
ax.plot(x, y, linestyle="dotted", color="grey")
y = get_y(ols["a"], ols["b"])
ax.plot(x, y, color="red", label="OLS")
ax.scatter(data.income, data.foodexp, alpha=0.2)
ax.set_xlim((240, 3000))
ax.set_ylim((240, 2000))
legend = ax.legend()
ax.set_xlabel("Income", fontsize=16)
ax.set_ylabel("Food expenditure", fontsize=16)
[5]:
Text(0, 0.5, 'Food expenditure')
第二个图¶
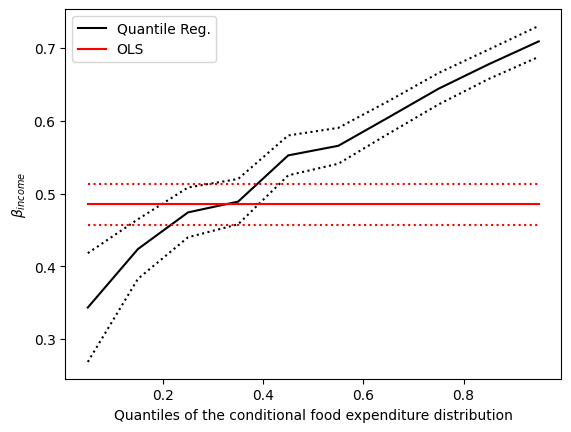
黑色虚线形成 10 个分位数回归估计(黑色实线)周围的 95% 点置信区间。红色线代表 OLS 回归结果及其 95% 置信区间。
在大多数情况下,分位数回归点估计位于 OLS 置信区间之外,这表明收入对食品支出的影响可能在整个分布中并不恒定。
[6]:
n = models.shape[0]
p1 = plt.plot(models.q, models.b, color="black", label="Quantile Reg.")
p2 = plt.plot(models.q, models.ub, linestyle="dotted", color="black")
p3 = plt.plot(models.q, models.lb, linestyle="dotted", color="black")
p4 = plt.plot(models.q, [ols["b"]] * n, color="red", label="OLS")
p5 = plt.plot(models.q, [ols["lb"]] * n, linestyle="dotted", color="red")
p6 = plt.plot(models.q, [ols["ub"]] * n, linestyle="dotted", color="red")
plt.ylabel(r"$\beta_{income}$")
plt.xlabel("Quantiles of the conditional food expenditure distribution")
plt.legend()
plt.show()
最后更新:2024 年 10 月 3 日