递归最小二乘法¶
递归最小二乘法是普通最小二乘法的扩展窗口版本。除了递归计算的回归系数的可用性之外,递归计算的残差还有助于构建统计数据来调查参数的不稳定性。
该 RecursiveLS 类允许计算递归残差并计算 CUSUM 和 CUSUM 平方统计量。将这些统计量与表示参数稳定性零假设的统计显着偏差的参考线一起绘制,可以轻松地直观地指示参数稳定性。
最后,该 RecursiveLS 模型允许对参数向量施加线性约束,并且可以使用公式接口构建。
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from pandas_datareader.data import DataReader
np.set_printoptions(suppress=True)
示例 1:铜¶
我们首先考虑铜数据集(以下描述)中的参数稳定性。
[2]:
print(sm.datasets.copper.DESCRLONG)
dta = sm.datasets.copper.load_pandas().data
dta.index = pd.date_range("1951-01-01", "1975-01-01", freq="YS")
endog = dta["WORLDCONSUMPTION"]
# To the regressors in the dataset, we add a column of ones for an intercept
exog = sm.add_constant(
dta[["COPPERPRICE", "INCOMEINDEX", "ALUMPRICE", "INVENTORYINDEX"]]
)
This data describes the world copper market from 1951 through 1975. In an
example, in Gill, the outcome variable (of a 2 stage estimation) is the world
consumption of copper for the 25 years. The explanatory variables are the
world consumption of copper in 1000 metric tons, the constant dollar adjusted
price of copper, the price of a substitute, aluminum, an index of real per
capita income base 1970, an annual measure of manufacturer inventory change,
and a time trend.
首先,构建并拟合模型,并打印摘要。尽管 RLS 模型递归地计算回归参数,因此与数据点一样多的估计,但摘要表仅显示对整个样本估计的回归参数;除了来自递归初始化的小影响外,这些估计等效于 OLS 估计。
[3]:
mod = sm.RecursiveLS(endog, exog)
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: WORLDCONSUMPTION No. Observations: 25
Model: RecursiveLS Log Likelihood -154.720
Date: Thu, 03 Oct 2024 R-squared: 0.965
Time: 15:46:06 AIC 319.441
Sample: 01-01-1951 BIC 325.535
- 01-01-1975 HQIC 321.131
Covariance Type: nonrobust Scale 117717.127
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
const -6562.3719 2378.939 -2.759 0.006 -1.12e+04 -1899.737
COPPERPRICE -13.8132 15.041 -0.918 0.358 -43.292 15.666
INCOMEINDEX 1.21e+04 763.401 15.853 0.000 1.06e+04 1.36e+04
ALUMPRICE 70.4146 32.678 2.155 0.031 6.367 134.462
INVENTORYINDEX 311.7330 2130.084 0.146 0.884 -3863.155 4486.621
===================================================================================
Ljung-Box (L1) (Q): 2.17 Jarque-Bera (JB): 1.70
Prob(Q): 0.14 Prob(JB): 0.43
Heteroskedasticity (H): 3.38 Skew: -0.67
Prob(H) (two-sided): 0.13 Kurtosis: 2.53
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
递归系数在 recursive_coefficients 属性中可用。或者,可以使用 plot_recursive_coefficient 方法生成绘图。
[4]:
print(res.recursive_coefficients.filtered[0])
res.plot_recursive_coefficient(range(mod.k_exog), alpha=None, figsize=(10, 6))
[ 2.88890087 4.94795049 1558.41803044 1958.43326658
-51474.9578655 -4168.94974192 -2252.61351128 -446.55908507
-5288.39794736 -6942.31935786 -7846.0890355 -6643.15121393
-6274.11015558 -7272.01696292 -6319.02648554 -5822.23929148
-6256.30902754 -6737.4044603 -6477.42841448 -5995.90746904
-6450.80677813 -6022.92166487 -5258.35152753 -5320.89136363
-6562.37193573]
[4]:
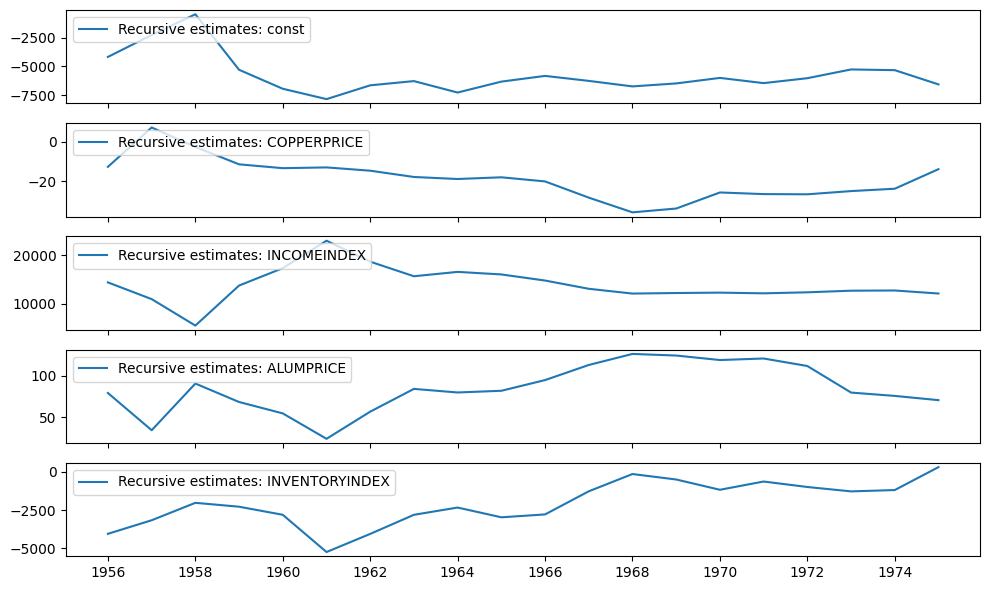
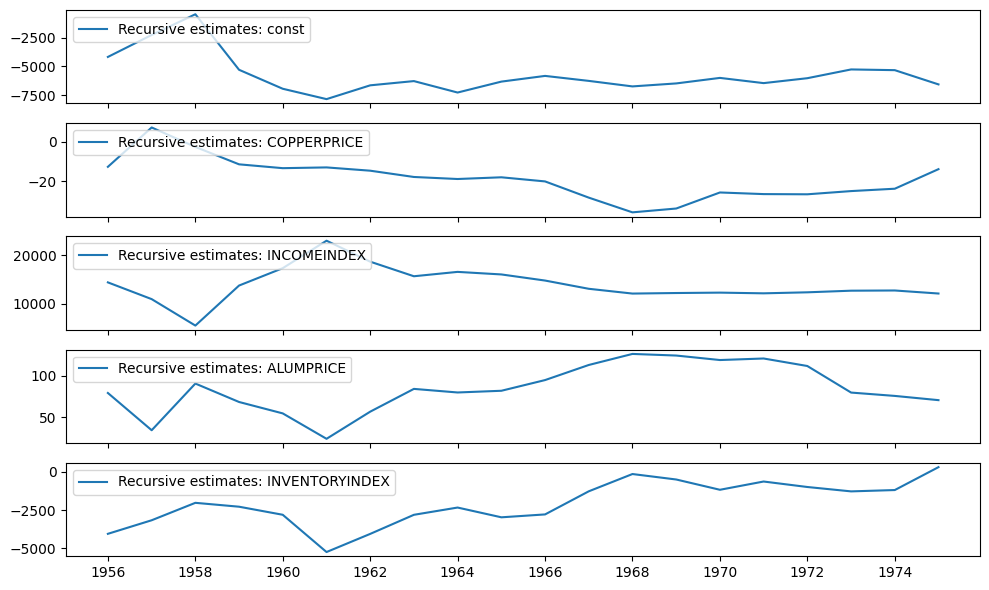
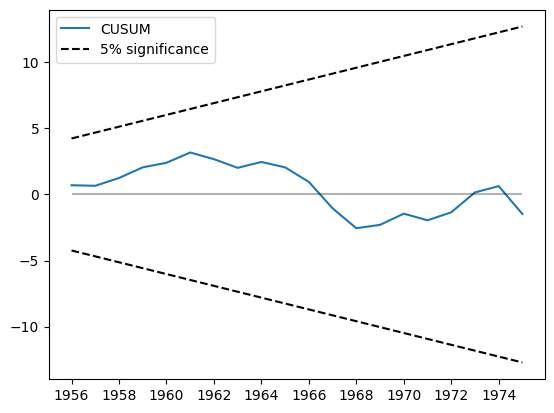
CUSUM 统计量在 cusum 属性中可用,但通常使用 plot_cusum 方法直观地检查参数稳定性更方便。在下图中,CUSUM 统计量没有超出 5% 的显著性带,因此我们在 5% 的水平上无法拒绝参数稳定的零假设。
[5]:
print(res.cusum)
fig = res.plot_cusum()
[ 0.69971508 0.65841244 1.24629674 2.05476032 2.39888918 3.1786198
2.67244672 2.01783215 2.46131747 2.05268638 0.95054336 -1.04505546
-2.55465286 -2.29908152 -1.45289492 -1.95353993 -1.3504662 0.15789829
0.6328653 -1.48184586]
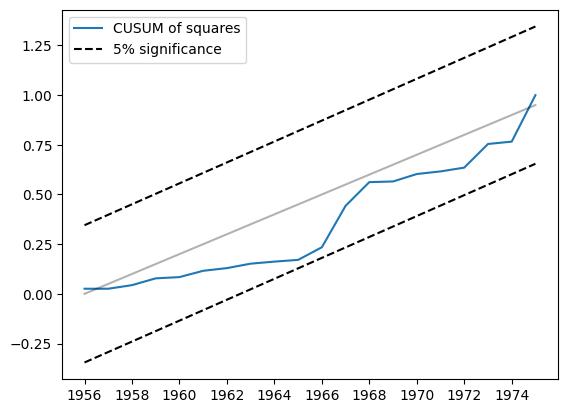
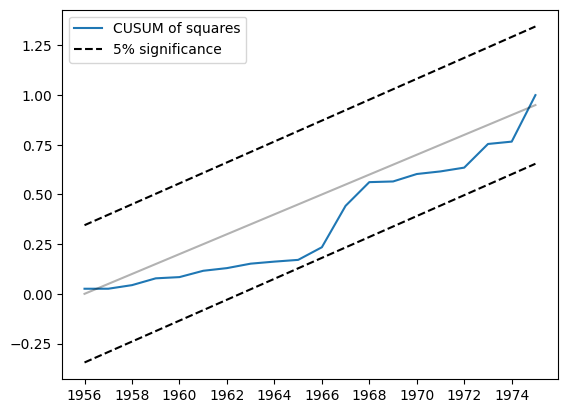
另一个相关的统计量是 CUSUM 平方。它在 cusum_squares 属性中可用,但同样,使用 plot_cusum_squares 方法直观地检查它更方便。在下图中,CUSUM 平方统计量没有超出 5% 的显著性带,因此我们在 5% 的水平上无法拒绝参数稳定的零假设。
[6]:
res.plot_cusum_squares()
[6]:
示例 2:货币数量论¶
货币数量论认为,“货币数量变化率的任何变化都会…导致…价格通货膨胀率的相同变化”(Lucas,1980)。继 Lucas 的思路,我们研究了货币增长双边指数加权移动平均值与 CPI 通货膨胀率之间的关系。尽管 Lucas 发现这些变量之间的关系是稳定的,但最近看来,这种关系是不稳定的;例如,参见 Sargent 和 Surico(2010)。
[7]:
start = "1959-12-01"
end = "2015-01-01"
m2 = DataReader("M2SL", "fred", start=start, end=end)
cpi = DataReader("CPIAUCSL", "fred", start=start, end=end)
[8]:
def ewma(series, beta, n_window):
nobs = len(series)
scalar = (1 - beta) / (1 + beta)
ma = []
k = np.arange(n_window, 0, -1)
weights = np.r_[beta ** k, 1, beta ** k[::-1]]
for t in range(n_window, nobs - n_window):
window = series.iloc[t - n_window : t + n_window + 1].values
ma.append(scalar * np.sum(weights * window))
return pd.Series(ma, name=series.name, index=series.iloc[n_window:-n_window].index)
m2_ewma = ewma(np.log(m2["M2SL"].resample("QS").mean()).diff().iloc[1:], 0.95, 10 * 4)
cpi_ewma = ewma(
np.log(cpi["CPIAUCSL"].resample("QS").mean()).diff().iloc[1:], 0.95, 10 * 4
)
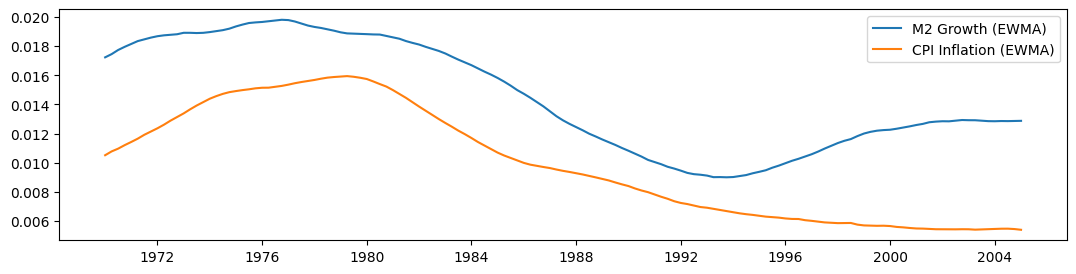
在使用 Lucas 的 \(\beta = 0.95\) 滤波器(两边各 10 年的窗口)构建移动平均值后,我们在下面绘制每个序列。虽然它们似乎在样本的一部分时间内一起移动,但在 1990 年之后,它们似乎开始发散。
[9]:
fig, ax = plt.subplots(figsize=(13, 3))
ax.plot(m2_ewma, label="M2 Growth (EWMA)")
ax.plot(cpi_ewma, label="CPI Inflation (EWMA)")
ax.legend()
[9]:
<matplotlib.legend.Legend at 0x7f6e8ca133a0>
[10]:
endog = cpi_ewma
exog = sm.add_constant(m2_ewma)
exog.columns = ["const", "M2"]
mod = sm.RecursiveLS(endog, exog)
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: CPIAUCSL No. Observations: 141
Model: RecursiveLS Log Likelihood 692.878
Date: Thu, 03 Oct 2024 R-squared: 0.813
Time: 15:46:11 AIC -1381.755
Sample: 01-01-1970 BIC -1375.858
- 01-01-2005 HQIC -1379.358
Covariance Type: nonrobust Scale 0.000
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0034 0.001 -6.013 0.000 -0.004 -0.002
M2 0.9128 0.037 24.601 0.000 0.840 0.986
===================================================================================
Ljung-Box (L1) (Q): 138.23 Jarque-Bera (JB): 18.20
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 5.30 Skew: -0.81
Prob(H) (two-sided): 0.00 Kurtosis: 2.27
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
[11]:
res.plot_recursive_coefficient(1, alpha=None)
[11]:
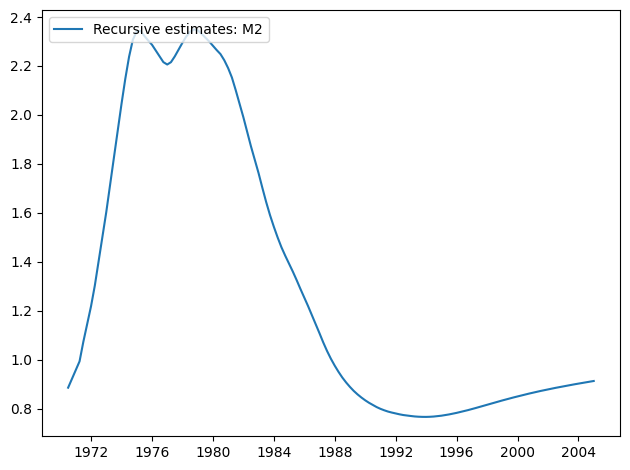
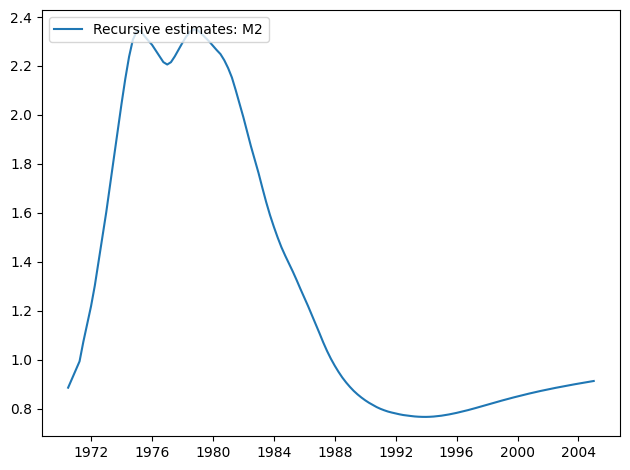
CUSUM 图现在显示出在 5% 水平上的重大偏差,表明拒绝参数稳定性的零假设。
[12]:
res.plot_cusum()
[12]:
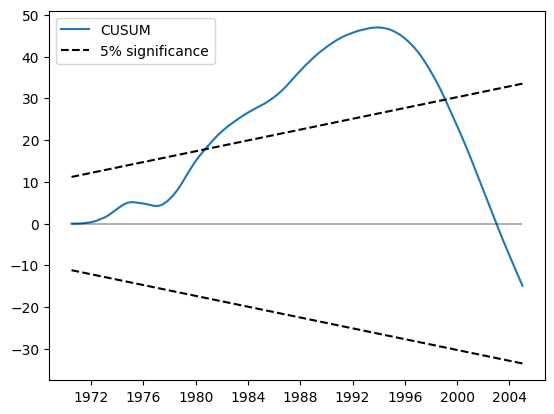
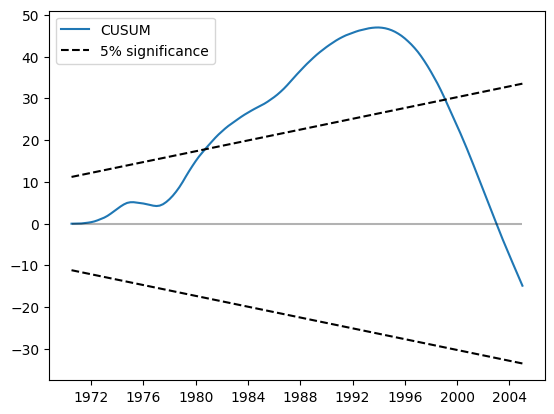
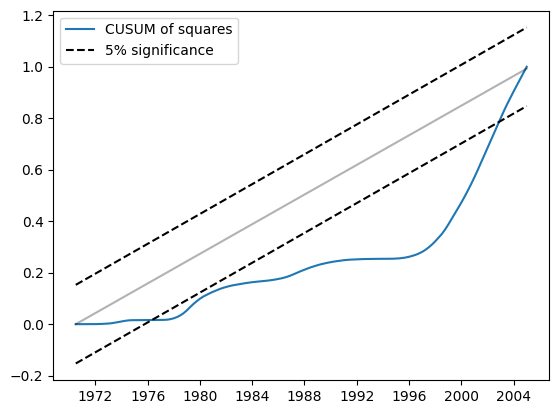
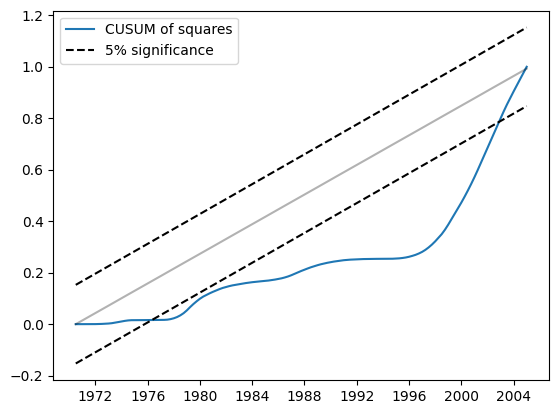
类似地,CUSUM 平方显示出在 5% 水平上的重大偏差,也表明拒绝参数稳定性的零假设。
[13]:
res.plot_cusum_squares()
[13]:
示例 3:线性约束和公式¶
线性约束¶
使用 constraints 参数在构建模型时,实现线性约束并不难。
[14]:
endog = dta["WORLDCONSUMPTION"]
exog = sm.add_constant(
dta[["COPPERPRICE", "INCOMEINDEX", "ALUMPRICE", "INVENTORYINDEX"]]
)
mod = sm.RecursiveLS(endog, exog, constraints="COPPERPRICE = ALUMPRICE")
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: WORLDCONSUMPTION No. Observations: 25
Model: RecursiveLS Log Likelihood -134.231
Date: Thu, 03 Oct 2024 R-squared: 0.989
Time: 15:46:14 AIC 276.462
Sample: 01-01-1951 BIC 281.338
- 01-01-1975 HQIC 277.814
Covariance Type: nonrobust Scale 137155.014
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
const -4839.4836 2412.410 -2.006 0.045 -9567.721 -111.246
COPPERPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INCOMEINDEX 1.115e+04 666.308 16.738 0.000 9847.000 1.25e+04
ALUMPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INVENTORYINDEX 241.3452 2298.951 0.105 0.916 -4264.515 4747.206
===================================================================================
Ljung-Box (L1) (Q): 6.27 Jarque-Bera (JB): 1.78
Prob(Q): 0.01 Prob(JB): 0.41
Heteroskedasticity (H): 1.75 Skew: -0.63
Prob(H) (two-sided): 0.48 Kurtosis: 2.32
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
公式¶
可以使用类方法 from_formula 拟合相同模型。
[15]:
mod = sm.RecursiveLS.from_formula(
"WORLDCONSUMPTION ~ COPPERPRICE + INCOMEINDEX + ALUMPRICE + INVENTORYINDEX",
dta,
constraints="COPPERPRICE = ALUMPRICE",
)
res = mod.fit()
print(res.summary())
Statespace Model Results
==============================================================================
Dep. Variable: WORLDCONSUMPTION No. Observations: 25
Model: RecursiveLS Log Likelihood -134.231
Date: Thu, 03 Oct 2024 R-squared: 0.989
Time: 15:46:14 AIC 276.462
Sample: 01-01-1951 BIC 281.338
- 01-01-1975 HQIC 277.814
Covariance Type: nonrobust Scale 137155.014
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept -4839.4836 2412.410 -2.006 0.045 -9567.721 -111.246
COPPERPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INCOMEINDEX 1.115e+04 666.308 16.738 0.000 9847.000 1.25e+04
ALUMPRICE 5.9797 12.704 0.471 0.638 -18.921 30.880
INVENTORYINDEX 241.3452 2298.951 0.105 0.916 -4264.515 4747.206
===================================================================================
Ljung-Box (L1) (Q): 6.27 Jarque-Bera (JB): 1.78
Prob(Q): 0.01 Prob(JB): 0.41
Heteroskedasticity (H): 1.75 Skew: -0.63
Prob(H) (two-sided): 0.48 Kurtosis: 2.32
===================================================================================
Warnings:
[1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample.
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/base/tsa_model.py:473: ValueWarning: No frequency information was provided, so inferred frequency YS-JAN will be used.
self._init_dates(dates, freq)