时间序列模型中的确定性项¶
[1]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.rc("figure", figsize=(16, 9))
plt.rc("font", size=16)
基本用法¶
基本配置可以通过 DeterministicProcess 直接构建。这些可以包括一个常数、任意阶数的时间趋势以及季节性或傅里叶分量。
该过程需要一个索引,即完整样本(或样本内)的索引。
首先,我们初始化一个具有常数、线性时间趋势和 5 周期季节项的确定性过程。 in_sample 方法返回与索引匹配的完整值集。
[2]:
from statsmodels.tsa.deterministic import DeterministicProcess
index = pd.RangeIndex(0, 100)
det_proc = DeterministicProcess(index, constant=True, order=1, seasonal=True, period=5)
det_proc.in_sample()
[2]:
| const | trend | s(2,5) | s(3,5) | s(4,5) | s(5,5) | |
|---|---|---|---|---|---|---|
| 0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 1.0 | 2.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 2 | 1.0 | 3.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 3 | 1.0 | 4.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 4 | 1.0 | 5.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... |
| 95 | 1.0 | 96.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 96 | 1.0 | 97.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 97 | 1.0 | 98.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 98 | 1.0 | 99.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 99 | 1.0 | 100.0 | 0.0 | 0.0 | 0.0 | 1.0 |
100 行 × 6 列
out_of_sample 返回样本末尾之后的下一个 steps 值。
[3]:
det_proc.out_of_sample(15)
[3]:
| const | trend | s(2,5) | s(3,5) | s(4,5) | s(5,5) | |
|---|---|---|---|---|---|---|
| 100 | 1.0 | 101.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 101 | 1.0 | 102.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 102 | 1.0 | 103.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 103 | 1.0 | 104.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 104 | 1.0 | 105.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 105 | 1.0 | 106.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 106 | 1.0 | 107.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 107 | 1.0 | 108.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 108 | 1.0 | 109.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 109 | 1.0 | 110.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 110 | 1.0 | 111.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 111 | 1.0 | 112.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 112 | 1.0 | 113.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 113 | 1.0 | 114.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 114 | 1.0 | 115.0 | 0.0 | 0.0 | 0.0 | 1.0 |
range(start, stop) 也可以用于在任何范围内(包括样本内和样本外)生成确定性项。
备注¶
当索引为 pandas
DatetimeIndex或PeriodIndex时,则start和stop可以是类似日期的(字符串,例如,“2020-06-01”,或时间戳)或整数。stop始终包含在范围内。虽然这在 Python 中并不常见,但这是必要的,因为 statsmodels 和 Pandas 在处理类似日期的切片时都包含stop。
[4]:
det_proc.range(190, 210)
[4]:
| const | trend | s(2,5) | s(3,5) | s(4,5) | s(5,5) | |
|---|---|---|---|---|---|---|
| 190 | 1.0 | 191.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 191 | 1.0 | 192.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 192 | 1.0 | 193.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 193 | 1.0 | 194.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 194 | 1.0 | 195.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 195 | 1.0 | 196.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 196 | 1.0 | 197.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 197 | 1.0 | 198.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 198 | 1.0 | 199.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 199 | 1.0 | 200.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 200 | 1.0 | 201.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 201 | 1.0 | 202.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 202 | 1.0 | 203.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 203 | 1.0 | 204.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 204 | 1.0 | 205.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 205 | 1.0 | 206.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 206 | 1.0 | 207.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 207 | 1.0 | 208.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 208 | 1.0 | 209.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 209 | 1.0 | 210.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 210 | 1.0 | 211.0 | 0.0 | 0.0 | 0.0 | 0.0 |
使用类似日期的索引¶
接下来,我们使用 PeriodIndex 展示相同的步骤。
[5]:
index = pd.period_range("2020-03-01", freq="M", periods=60)
det_proc = DeterministicProcess(index, constant=True, fourier=2)
det_proc.in_sample().head(12)
[5]:
| const | sin(1,12) | cos(1,12) | sin(2,12) | cos(2,12) | |
|---|---|---|---|---|---|
| 2020-03 | 1.0 | 0.000000e+00 | 1.000000e+00 | 0.000000e+00 | 1.0 |
| 2020-04 | 1.0 | 5.000000e-01 | 8.660254e-01 | 8.660254e-01 | 0.5 |
| 2020-05 | 1.0 | 8.660254e-01 | 5.000000e-01 | 8.660254e-01 | -0.5 |
| 2020-06 | 1.0 | 1.000000e+00 | 6.123234e-17 | 1.224647e-16 | -1.0 |
| 2020-07 | 1.0 | 8.660254e-01 | -5.000000e-01 | -8.660254e-01 | -0.5 |
| 2020-08 | 1.0 | 5.000000e-01 | -8.660254e-01 | -8.660254e-01 | 0.5 |
| 2020-09 | 1.0 | 1.224647e-16 | -1.000000e+00 | -2.449294e-16 | 1.0 |
| 2020-10 | 1.0 | -5.000000e-01 | -8.660254e-01 | 8.660254e-01 | 0.5 |
| 2020-11 | 1.0 | -8.660254e-01 | -5.000000e-01 | 8.660254e-01 | -0.5 |
| 2020-12 | 1.0 | -1.000000e+00 | -1.836970e-16 | 3.673940e-16 | -1.0 |
| 2021-01 | 1.0 | -8.660254e-01 | 5.000000e-01 | -8.660254e-01 | -0.5 |
| 2021-02 | 1.0 | -5.000000e-01 | 8.660254e-01 | -8.660254e-01 | 0.5 |
[6]:
det_proc.out_of_sample(12)
[6]:
| const | sin(1,12) | cos(1,12) | sin(2,12) | cos(2,12) | |
|---|---|---|---|---|---|
| 2025-03 | 1.0 | -1.224647e-15 | 1.000000e+00 | -2.449294e-15 | 1.0 |
| 2025-04 | 1.0 | 5.000000e-01 | 8.660254e-01 | 8.660254e-01 | 0.5 |
| 2025-05 | 1.0 | 8.660254e-01 | 5.000000e-01 | 8.660254e-01 | -0.5 |
| 2025-06 | 1.0 | 1.000000e+00 | -4.904777e-16 | -9.809554e-16 | -1.0 |
| 2025-07 | 1.0 | 8.660254e-01 | -5.000000e-01 | -8.660254e-01 | -0.5 |
| 2025-08 | 1.0 | 5.000000e-01 | -8.660254e-01 | -8.660254e-01 | 0.5 |
| 2025-09 | 1.0 | 4.899825e-15 | -1.000000e+00 | -9.799650e-15 | 1.0 |
| 2025-10 | 1.0 | -5.000000e-01 | -8.660254e-01 | 8.660254e-01 | 0.5 |
| 2025-11 | 1.0 | -8.660254e-01 | -5.000000e-01 | 8.660254e-01 | -0.5 |
| 2025-12 | 1.0 | -1.000000e+00 | -3.184701e-15 | 6.369401e-15 | -1.0 |
| 2026-01 | 1.0 | -8.660254e-01 | 5.000000e-01 | -8.660254e-01 | -0.5 |
| 2026-02 | 1.0 | -5.000000e-01 | 8.660254e-01 | -8.660254e-01 | 0.5 |
range 接受类似日期的参数,这些参数通常以字符串形式给出。
[7]:
det_proc.range("2025-01", "2026-01")
[7]:
| const | sin(1,12) | cos(1,12) | sin(2,12) | cos(2,12) | |
|---|---|---|---|---|---|
| 2025-01 | 1.0 | -8.660254e-01 | 5.000000e-01 | -8.660254e-01 | -0.5 |
| 2025-02 | 1.0 | -5.000000e-01 | 8.660254e-01 | -8.660254e-01 | 0.5 |
| 2025-03 | 1.0 | -1.224647e-15 | 1.000000e+00 | -2.449294e-15 | 1.0 |
| 2025-04 | 1.0 | 5.000000e-01 | 8.660254e-01 | 8.660254e-01 | 0.5 |
| 2025-05 | 1.0 | 8.660254e-01 | 5.000000e-01 | 8.660254e-01 | -0.5 |
| 2025-06 | 1.0 | 1.000000e+00 | -4.904777e-16 | -9.809554e-16 | -1.0 |
| 2025-07 | 1.0 | 8.660254e-01 | -5.000000e-01 | -8.660254e-01 | -0.5 |
| 2025-08 | 1.0 | 5.000000e-01 | -8.660254e-01 | -8.660254e-01 | 0.5 |
| 2025-09 | 1.0 | 4.899825e-15 | -1.000000e+00 | -9.799650e-15 | 1.0 |
| 2025-10 | 1.0 | -5.000000e-01 | -8.660254e-01 | 8.660254e-01 | 0.5 |
| 2025-11 | 1.0 | -8.660254e-01 | -5.000000e-01 | 8.660254e-01 | -0.5 |
| 2025-12 | 1.0 | -1.000000e+00 | -3.184701e-15 | 6.369401e-15 | -1.0 |
| 2026-01 | 1.0 | -8.660254e-01 | 5.000000e-01 | -8.660254e-01 | -0.5 |
这等同于使用整数 58 和 70。
[8]:
det_proc.range(58, 70)
[8]:
| const | sin(1,12) | cos(1,12) | sin(2,12) | cos(2,12) | |
|---|---|---|---|---|---|
| 2025-01 | 1.0 | -8.660254e-01 | 5.000000e-01 | -8.660254e-01 | -0.5 |
| 2025-02 | 1.0 | -5.000000e-01 | 8.660254e-01 | -8.660254e-01 | 0.5 |
| 2025-03 | 1.0 | -1.224647e-15 | 1.000000e+00 | -2.449294e-15 | 1.0 |
| 2025-04 | 1.0 | 5.000000e-01 | 8.660254e-01 | 8.660254e-01 | 0.5 |
| 2025-05 | 1.0 | 8.660254e-01 | 5.000000e-01 | 8.660254e-01 | -0.5 |
| 2025-06 | 1.0 | 1.000000e+00 | -4.904777e-16 | -9.809554e-16 | -1.0 |
| 2025-07 | 1.0 | 8.660254e-01 | -5.000000e-01 | -8.660254e-01 | -0.5 |
| 2025-08 | 1.0 | 5.000000e-01 | -8.660254e-01 | -8.660254e-01 | 0.5 |
| 2025-09 | 1.0 | 4.899825e-15 | -1.000000e+00 | -9.799650e-15 | 1.0 |
| 2025-10 | 1.0 | -5.000000e-01 | -8.660254e-01 | 8.660254e-01 | 0.5 |
| 2025-11 | 1.0 | -8.660254e-01 | -5.000000e-01 | 8.660254e-01 | -0.5 |
| 2025-12 | 1.0 | -1.000000e+00 | -3.184701e-15 | 6.369401e-15 | -1.0 |
| 2026-01 | 1.0 | -8.660254e-01 | 5.000000e-01 | -8.660254e-01 | -0.5 |
高级构建¶
可以通过 additional_terms 创建具有构造函数不支持的功能的确定性过程,该参数接受 DetermisticTerm 的列表。在这里,我们创建一个具有两个季节性分量的确定性过程:具有 5 天周期的星期几,以及通过具有 365.25 天周期的傅里叶分量捕获的年度。
[9]:
from statsmodels.tsa.deterministic import Fourier, Seasonality, TimeTrend
index = pd.period_range("2020-03-01", freq="D", periods=2 * 365)
tt = TimeTrend(constant=True)
four = Fourier(period=365.25, order=2)
seas = Seasonality(period=7)
det_proc = DeterministicProcess(index, additional_terms=[tt, seas, four])
det_proc.in_sample().head(28)
[9]:
| const | s(2,7) | s(3,7) | s(4,7) | s(5,7) | s(6,7) | s(7,7) | sin(1,365.25) | cos(1,365.25) | sin(2,365.25) | cos(2,365.25) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-03-01 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 1.000000 | 0.000000 | 1.000000 |
| 2020-03-02 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.017202 | 0.999852 | 0.034398 | 0.999408 |
| 2020-03-03 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.034398 | 0.999408 | 0.068755 | 0.997634 |
| 2020-03-04 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.051584 | 0.998669 | 0.103031 | 0.994678 |
| 2020-03-05 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.068755 | 0.997634 | 0.137185 | 0.990545 |
| 2020-03-06 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.085906 | 0.996303 | 0.171177 | 0.985240 |
| 2020-03-07 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.103031 | 0.994678 | 0.204966 | 0.978769 |
| 2020-03-08 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.120126 | 0.992759 | 0.238513 | 0.971139 |
| 2020-03-09 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.137185 | 0.990545 | 0.271777 | 0.962360 |
| 2020-03-10 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.154204 | 0.988039 | 0.304719 | 0.952442 |
| 2020-03-11 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.171177 | 0.985240 | 0.337301 | 0.941397 |
| 2020-03-12 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.188099 | 0.982150 | 0.369484 | 0.929237 |
| 2020-03-13 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.204966 | 0.978769 | 0.401229 | 0.915978 |
| 2020-03-14 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.221772 | 0.975099 | 0.432499 | 0.901634 |
| 2020-03-15 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.238513 | 0.971139 | 0.463258 | 0.886224 |
| 2020-03-16 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.255182 | 0.966893 | 0.493468 | 0.869764 |
| 2020-03-17 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.271777 | 0.962360 | 0.523094 | 0.852275 |
| 2020-03-18 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.288291 | 0.957543 | 0.552101 | 0.833777 |
| 2020-03-19 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.304719 | 0.952442 | 0.580455 | 0.814292 |
| 2020-03-20 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.321058 | 0.947060 | 0.608121 | 0.793844 |
| 2020-03-21 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.337301 | 0.941397 | 0.635068 | 0.772456 |
| 2020-03-22 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.353445 | 0.935455 | 0.661263 | 0.750154 |
| 2020-03-23 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.369484 | 0.929237 | 0.686676 | 0.726964 |
| 2020-03-24 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.385413 | 0.922744 | 0.711276 | 0.702913 |
| 2020-03-25 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.401229 | 0.915978 | 0.735034 | 0.678031 |
| 2020-03-26 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.416926 | 0.908940 | 0.757922 | 0.652346 |
| 2020-03-27 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.432499 | 0.901634 | 0.779913 | 0.625889 |
| 2020-03-28 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.447945 | 0.894061 | 0.800980 | 0.598691 |
自定义确定性项¶
DetermisticTerm 抽象基类旨在被子类化,以帮助用户编写自定义确定性项。接下来,我们将展示两个示例。第一个是断裂时间趋势,它允许在固定数量的周期后断裂。第二个是“技巧”确定性项,它允许将外生数据(实际上不是确定性过程)视为确定性过程。这让我们可以简化收集预测所需的项。
这些旨在演示自定义项的构造。它们在输入验证方面肯定可以改进。
[10]:
from statsmodels.tsa.deterministic import DeterministicTerm
class BrokenTimeTrend(DeterministicTerm):
def __init__(self, break_period: int):
self._break_period = break_period
def __str__(self):
return "Broken Time Trend"
def _eq_attr(self):
return (self._break_period,)
def in_sample(self, index: pd.Index):
nobs = index.shape[0]
terms = np.zeros((nobs, 2))
terms[self._break_period :, 0] = 1
terms[self._break_period :, 1] = np.arange(self._break_period + 1, nobs + 1)
return pd.DataFrame(terms, columns=["const_break", "trend_break"], index=index)
def out_of_sample(
self, steps: int, index: pd.Index, forecast_index: pd.Index = None
):
# Always call extend index first
fcast_index = self._extend_index(index, steps, forecast_index)
nobs = index.shape[0]
terms = np.zeros((steps, 2))
# Assume break period is in-sample
terms[:, 0] = 1
terms[:, 1] = np.arange(nobs + 1, nobs + steps + 1)
return pd.DataFrame(
terms, columns=["const_break", "trend_break"], index=fcast_index
)
[11]:
btt = BrokenTimeTrend(60)
tt = TimeTrend(constant=True, order=1)
index = pd.RangeIndex(100)
det_proc = DeterministicProcess(index, additional_terms=[tt, btt])
det_proc.range(55, 65)
[11]:
| const | trend | const_break | trend_break | |
|---|---|---|---|---|
| 55 | 1.0 | 56.0 | 0.0 | 0.0 |
| 56 | 1.0 | 57.0 | 0.0 | 0.0 |
| 57 | 1.0 | 58.0 | 0.0 | 0.0 |
| 58 | 1.0 | 59.0 | 0.0 | 0.0 |
| 59 | 1.0 | 60.0 | 0.0 | 0.0 |
| 60 | 1.0 | 61.0 | 1.0 | 61.0 |
| 61 | 1.0 | 62.0 | 1.0 | 62.0 |
| 62 | 1.0 | 63.0 | 1.0 | 63.0 |
| 63 | 1.0 | 64.0 | 1.0 | 64.0 |
| 64 | 1.0 | 65.0 | 1.0 | 65.0 |
| 65 | 1.0 | 66.0 | 1.0 | 66.0 |
接下来,我们为一些实际外生数据编写一个简单的“包装器”,以简化构建用于预测的样本外外生数组。
[12]:
class ExogenousProcess(DeterministicTerm):
def __init__(self, data):
self._data = data
def __str__(self):
return "Custom Exog Process"
def _eq_attr(self):
return (id(self._data),)
def in_sample(self, index: pd.Index):
return self._data.loc[index]
def out_of_sample(
self, steps: int, index: pd.Index, forecast_index: pd.Index = None
):
forecast_index = self._extend_index(index, steps, forecast_index)
return self._data.loc[forecast_index]
[13]:
import numpy as np
gen = np.random.default_rng(98765432101234567890)
exog = pd.DataFrame(gen.integers(100, size=(300, 2)), columns=["exog1", "exog2"])
exog.head()
[13]:
| exog1 | exog2 | |
|---|---|---|
| 0 | 6 | 99 |
| 1 | 64 | 28 |
| 2 | 15 | 81 |
| 3 | 54 | 8 |
| 4 | 12 | 8 |
[14]:
ep = ExogenousProcess(exog)
tt = TimeTrend(constant=True, order=1)
# The in-sample index
idx = exog.index[:200]
det_proc = DeterministicProcess(idx, additional_terms=[tt, ep])
[15]:
det_proc.in_sample().head()
[15]:
| const | trend | exog1 | exog2 | |
|---|---|---|---|---|
| 0 | 1.0 | 1.0 | 6 | 99 |
| 1 | 1.0 | 2.0 | 64 | 28 |
| 2 | 1.0 | 3.0 | 15 | 81 |
| 3 | 1.0 | 4.0 | 54 | 8 |
| 4 | 1.0 | 5.0 | 12 | 8 |
[16]:
det_proc.out_of_sample(10)
[16]:
| const | trend | exog1 | exog2 | |
|---|---|---|---|---|
| 200 | 1.0 | 201.0 | 56 | 88 |
| 201 | 1.0 | 202.0 | 48 | 84 |
| 202 | 1.0 | 203.0 | 44 | 5 |
| 203 | 1.0 | 204.0 | 65 | 63 |
| 204 | 1.0 | 205.0 | 63 | 39 |
| 205 | 1.0 | 206.0 | 89 | 39 |
| 206 | 1.0 | 207.0 | 41 | 54 |
| 207 | 1.0 | 208.0 | 71 | 5 |
| 208 | 1.0 | 209.0 | 89 | 6 |
| 209 | 1.0 | 210.0 | 58 | 63 |
模型支持¶
唯一直接支持 DeterministicProcess 的模型是 AutoReg。可以使用 deterministic 关键字参数设置自定义项。
注意:使用自定义项要求 trend="n" 和 seasonal=False,以便所有确定性分量都必须来自自定义确定性项。
模拟一些数据¶
在这里,我们模拟一些数据,这些数据具有通过傅里叶级数捕获的每周季节性。
[17]:
gen = np.random.default_rng(98765432101234567890)
idx = pd.RangeIndex(200)
det_proc = DeterministicProcess(idx, constant=True, period=52, fourier=2)
det_terms = det_proc.in_sample().to_numpy()
params = np.array([1.0, 3, -1, 4, -2])
exog = det_terms @ params
y = np.empty(200)
y[0] = det_terms[0] @ params + gen.standard_normal()
for i in range(1, 200):
y[i] = 0.9 * y[i - 1] + det_terms[i] @ params + gen.standard_normal()
y = pd.Series(y, index=idx)
ax = y.plot()
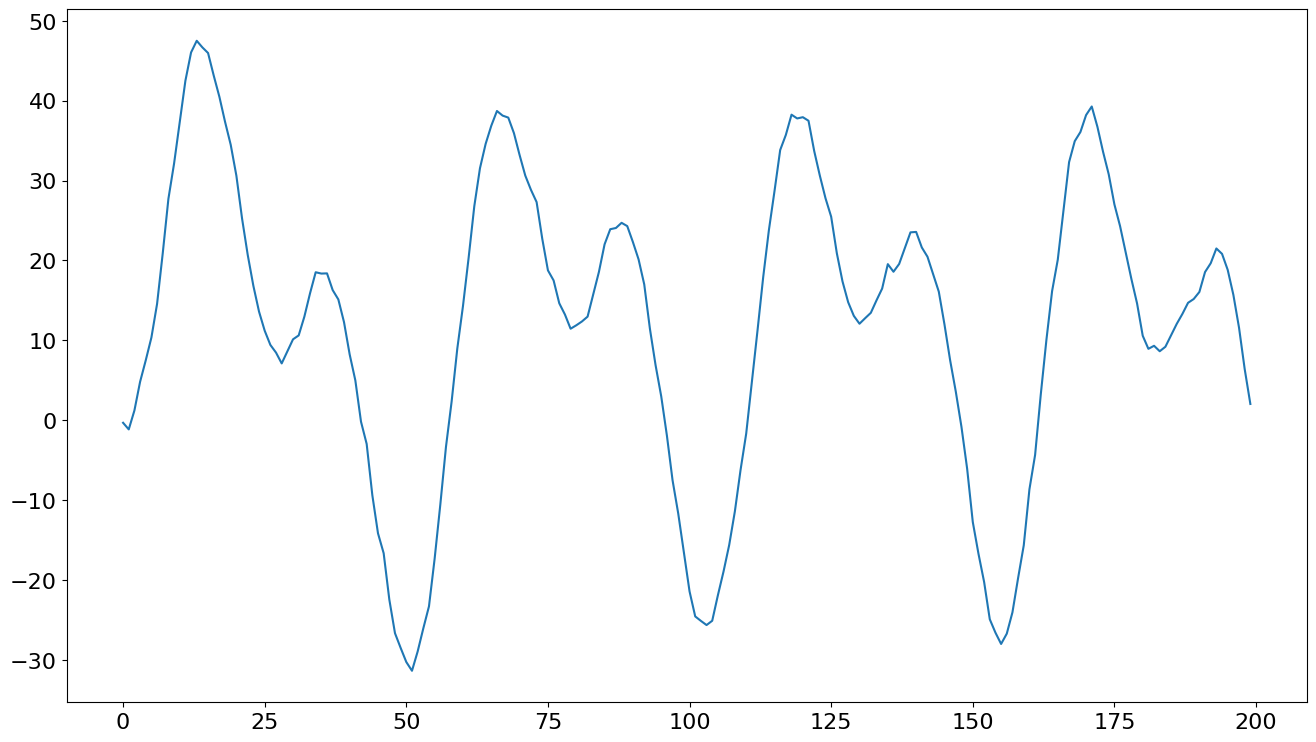
然后使用 deterministic 关键字参数拟合模型。 seasonal 默认值为 False,但 trend 默认值为 "c",因此需要更改此值。
[18]:
from statsmodels.tsa.api import AutoReg
mod = AutoReg(y, 1, trend="n", deterministic=det_proc)
res = mod.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: y No. Observations: 200
Model: AutoReg(1) Log Likelihood -270.964
Method: Conditional MLE S.D. of innovations 0.944
Date: Thu, 03 Oct 2024 AIC 555.927
Time: 15:46:43 BIC 578.980
Sample: 1 HQIC 565.258
200
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.8436 0.172 4.916 0.000 0.507 1.180
sin(1,52) 2.9738 0.160 18.587 0.000 2.660 3.287
cos(1,52) -0.6771 0.284 -2.380 0.017 -1.235 -0.120
sin(2,52) 3.9951 0.099 40.336 0.000 3.801 4.189
cos(2,52) -1.7206 0.264 -6.519 0.000 -2.238 -1.203
y.L1 0.9116 0.014 63.264 0.000 0.883 0.940
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0970 +0.0000j 1.0970 0.0000
-----------------------------------------------------------------------------
我们可以使用 plot_predict 显示预测值及其预测区间。样本外确定性值由传递给 AutoReg 的确定性过程自动生成。
[19]:
fig = res.plot_predict(200, 200 + 2 * 52, True)
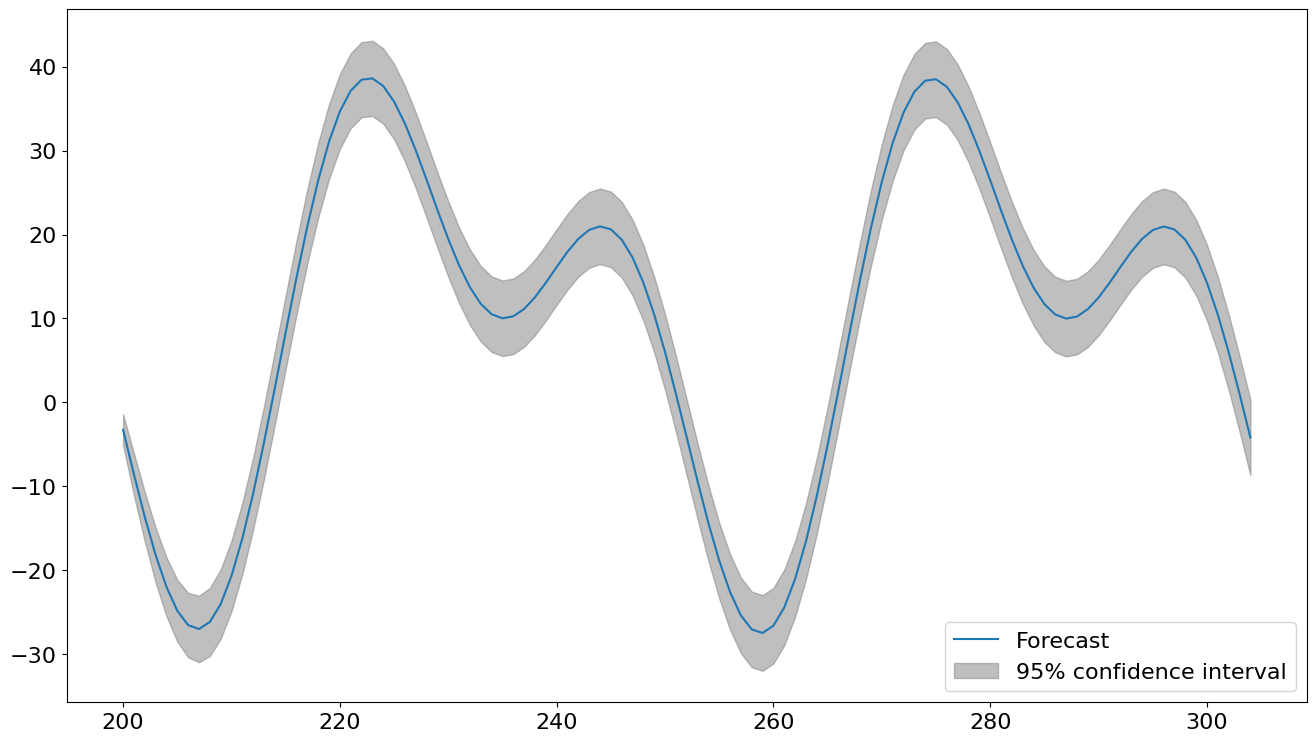
[20]:
auto_reg_forecast = res.predict(200, 211)
auto_reg_forecast
[20]:
200 -3.253482
201 -8.555660
202 -13.607557
203 -18.152622
204 -21.950370
205 -24.790116
206 -26.503171
207 -26.972781
208 -26.141244
209 -24.013773
210 -20.658891
211 -16.205310
dtype: float64
与其他模型一起使用¶
其他模型不支持直接 DeterministicProcess。相反,我们可以手动将任何确定性项作为 exog 传递给支持外生值的模型。
请注意,具有外生变量的 SARIMAX 是具有 SARIMA 误差的 OLS,因此模型为
确定性项上的参数与 AutoReg 的参数不直接可比,后者根据以下等式演变
当 \(x_t\) 仅包含确定性项时,这两种表示形式是等效的(假设 \(\theta(L)=0\),因此没有 MA)。
[21]:
from statsmodels.tsa.api import SARIMAX
det_proc = DeterministicProcess(idx, period=52, fourier=2)
det_terms = det_proc.in_sample()
mod = SARIMAX(y, order=(1, 0, 0), trend="c", exog=det_terms)
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 200
Model: SARIMAX(1, 0, 0) Log Likelihood -293.381
Date: Thu, 03 Oct 2024 AIC 600.763
Time: 15:46:44 BIC 623.851
Sample: 0 HQIC 610.106
- 200
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0796 0.140 0.567 0.571 -0.196 0.355
sin(1,52) 9.1917 0.876 10.492 0.000 7.475 10.909
cos(1,52) -17.4351 0.891 -19.576 0.000 -19.181 -15.689
sin(2,52) 1.2509 0.466 2.683 0.007 0.337 2.165
cos(2,52) -17.1865 0.434 -39.582 0.000 -18.038 -16.335
ar.L1 0.9957 0.007 150.751 0.000 0.983 1.009
sigma2 1.0748 0.119 9.067 0.000 0.842 1.307
===================================================================================
Ljung-Box (L1) (Q): 2.16 Jarque-Bera (JB): 1.03
Prob(Q): 0.14 Prob(JB): 0.60
Heteroskedasticity (H): 0.71 Skew: -0.14
Prob(H) (two-sided): 0.16 Kurtosis: 2.78
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
预测相似,但不同,因为 SARIMAX 的参数使用 MLE 估计,而 AutoReg 使用 OLS。
[22]:
sarimax_forecast = res.forecast(12, exog=det_proc.out_of_sample(12))
df = pd.concat([auto_reg_forecast, sarimax_forecast], axis=1)
df.columns = columns = ["AutoReg", "SARIMAX"]
df
[22]:
| AutoReg | SARIMAX | |
|---|---|---|
| 200 | -3.253482 | -2.956589 |
| 201 | -8.555660 | -7.985653 |
| 202 | -13.607557 | -12.794185 |
| 203 | -18.152622 | -17.131131 |
| 204 | -21.950370 | -20.760701 |
| 205 | -24.790116 | -23.475800 |
| 206 | -26.503171 | -25.109977 |
| 207 | -26.972781 | -25.547191 |
| 208 | -26.141244 | -24.728829 |
| 209 | -24.013773 | -22.657570 |
| 210 | -20.658891 | -19.397843 |
| 211 | -16.205310 | -15.072875 |