指数平滑

让我们考虑 Hyndman 和 Athanasopoulos [1] 关于指数平滑主题的优秀论著中的第 7 章。我们将按照他们展开的方式完成本章的所有示例。

[1] Hyndman, Rob J. 和 George Athanasopoulos。预测：原理与实践。OTexts，2014 年。

加载数据

首先我们加载一些数据。为了方便起见，我们在笔记本中包含了 R 数据。

[1]:

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt

%matplotlib inline

data = [
    446.6565,
    454.4733,
    455.663,
    423.6322,
    456.2713,
    440.5881,
    425.3325,
    485.1494,
    506.0482,
    526.792,
    514.2689,
    494.211,
]
index = pd.date_range(start="1996", end="2008", freq="Y")
oildata = pd.Series(data, index)

data = [
    17.5534,
    21.86,
    23.8866,
    26.9293,
    26.8885,
    28.8314,
    30.0751,
    30.9535,
    30.1857,
    31.5797,
    32.5776,
    33.4774,
    39.0216,
    41.3864,
    41.5966,
]
index = pd.date_range(start="1990", end="2005", freq="Y")
air = pd.Series(data, index)

data = [
    263.9177,
    268.3072,
    260.6626,
    266.6394,
    277.5158,
    283.834,
    290.309,
    292.4742,
    300.8307,
    309.2867,
    318.3311,
    329.3724,
    338.884,
    339.2441,
    328.6006,
    314.2554,
    314.4597,
    321.4138,
    329.7893,
    346.3852,
    352.2979,
    348.3705,
    417.5629,
    417.1236,
    417.7495,
    412.2339,
    411.9468,
    394.6971,
    401.4993,
    408.2705,
    414.2428,
]
index = pd.date_range(start="1970", end="2001", freq="Y")
livestock2 = pd.Series(data, index)

data = [407.9979, 403.4608, 413.8249, 428.105, 445.3387, 452.9942, 455.7402]
index = pd.date_range(start="2001", end="2008", freq="Y")
livestock3 = pd.Series(data, index)

data = [
    41.7275,
    24.0418,
    32.3281,
    37.3287,
    46.2132,
    29.3463,
    36.4829,
    42.9777,
    48.9015,
    31.1802,
    37.7179,
    40.4202,
    51.2069,
    31.8872,
    40.9783,
    43.7725,
    55.5586,
    33.8509,
    42.0764,
    45.6423,
    59.7668,
    35.1919,
    44.3197,
    47.9137,
]
index = pd.date_range(start="2005", end="2010-Q4", freq="QS-OCT")
aust = pd.Series(data, index)

/tmp/ipykernel_3946/536270367.py:23: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="1996", end="2008", freq="Y")
/tmp/ipykernel_3946/536270367.py:43: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="1990", end="2005", freq="Y")
/tmp/ipykernel_3946/536270367.py:79: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="1970", end="2001", freq="Y")
/tmp/ipykernel_3946/536270367.py:83: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="2001", end="2008", freq="Y")

简单指数平滑

让我们使用简单指数平滑来预测以下石油数据。

[2]:

ax = oildata.plot()
ax.set_xlabel("Year")
ax.set_ylabel("Oil (millions of tonnes)")
print("Figure 7.1: Oil production in Saudi Arabia from 1996 to 2007.")

Figure 7.1: Oil production in Saudi Arabia from 1996 to 2007.
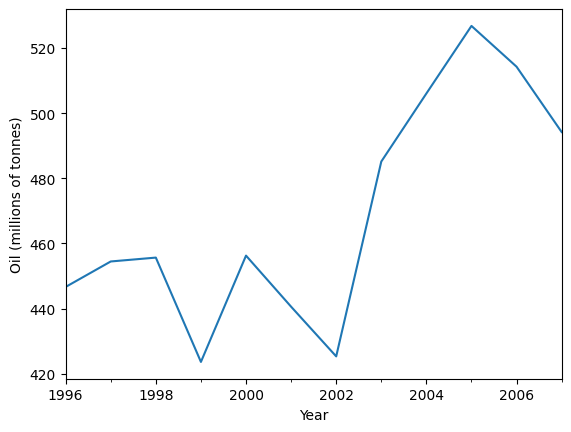
../../../_images/examples_notebooks_generated_exponential_smoothing_4_1.png

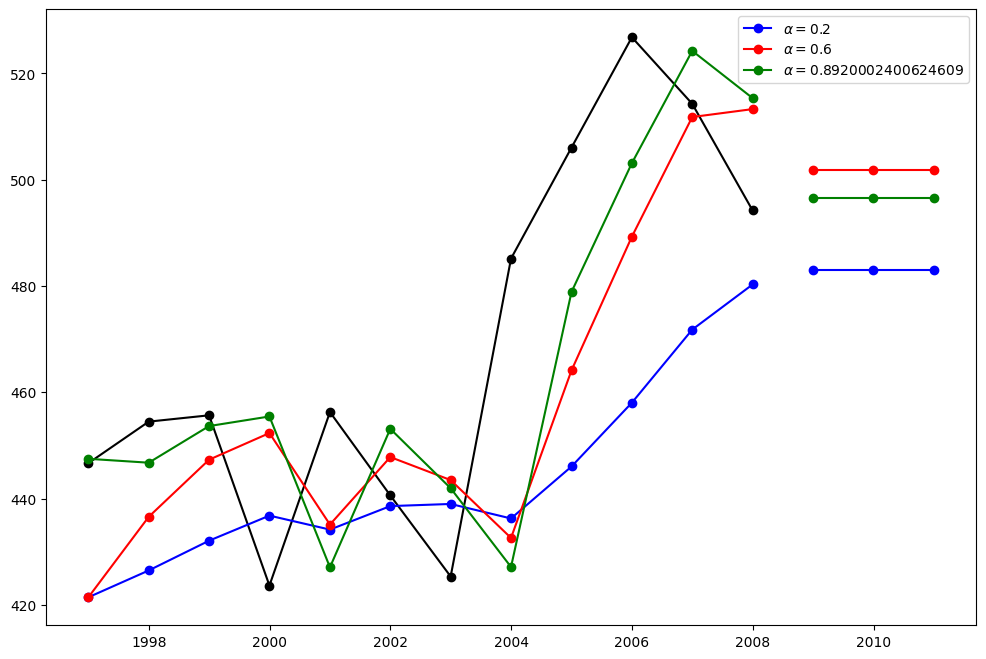
在这里，我们运行三种简单指数平滑的变体：1. 在 fit1 中，我们不使用自动优化，而是选择显式地为模型提供 \(\alpha=0.2\) 参数 2. 在 fit2 中，我们选择使用 \(\alpha=0.6\) 3. 在 fit3 中，我们允许 statsmodels 为我们自动找到一个优化的 \(\alpha\) 值。这是推荐的方法。

[3]:

fit1 = SimpleExpSmoothing(oildata, initialization_method="heuristic").fit(
    smoothing_level=0.2, optimized=False
)
fcast1 = fit1.forecast(3).rename(r"$\alpha=0.2$")
fit2 = SimpleExpSmoothing(oildata, initialization_method="heuristic").fit(
    smoothing_level=0.6, optimized=False
)
fcast2 = fit2.forecast(3).rename(r"$\alpha=0.6$")
fit3 = SimpleExpSmoothing(oildata, initialization_method="estimated").fit()
fcast3 = fit3.forecast(3).rename(r"$\alpha=%s$" % fit3.model.params["smoothing_level"])

plt.figure(figsize=(12, 8))
plt.plot(oildata, marker="o", color="black")
plt.plot(fit1.fittedvalues, marker="o", color="blue")
(line1,) = plt.plot(fcast1, marker="o", color="blue")
plt.plot(fit2.fittedvalues, marker="o", color="red")
(line2,) = plt.plot(fcast2, marker="o", color="red")
plt.plot(fit3.fittedvalues, marker="o", color="green")
(line3,) = plt.plot(fcast3, marker="o", color="green")
plt.legend([line1, line2, line3], [fcast1.name, fcast2.name, fcast3.name])

[3]:

<matplotlib.legend.Legend at 0x7f4b3edd1930>
../../../_images/examples_notebooks_generated_exponential_smoothing_6_1.png

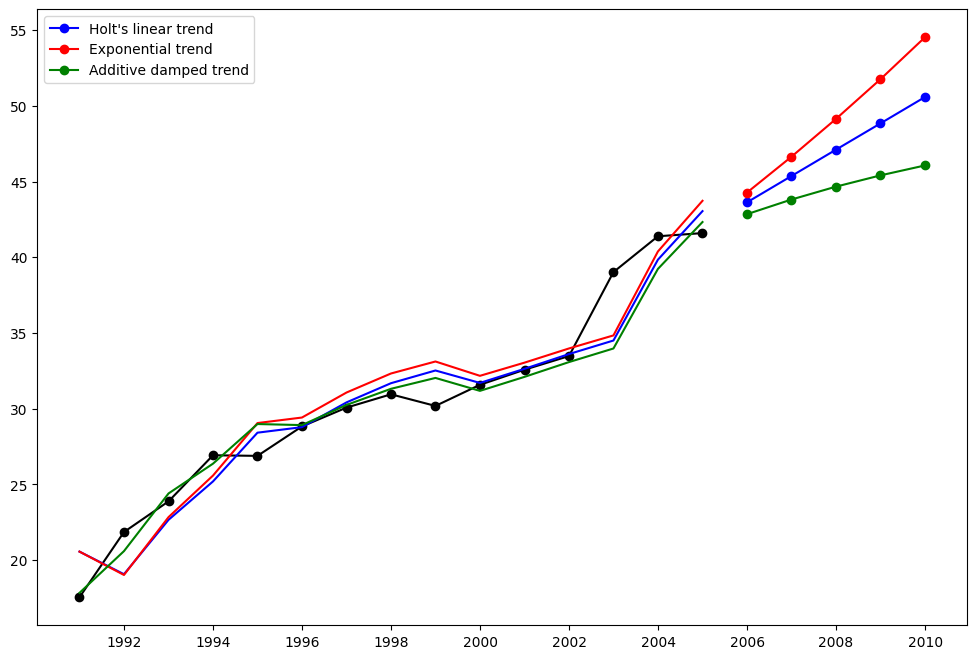
霍尔特方法

让我们看看另一个例子。这次我们使用空气污染数据和霍尔特方法。我们将再次拟合三个例子。1. 在 fit1 中，我们再次选择不使用优化器，并为 \(\alpha=0.8\) 和 \(\beta=0.2\) 提供显式值 2. 在 fit2 中，我们与 fit1 中一样，选择使用指数模型而不是霍尔特的加法模型。 3. 在 fit3 中，我们使用霍尔特加法模型的阻尼版本，但在固定 \(\alpha=0.8\) 和 \(\beta=0.2\) 的值的同时，允许阻尼参数 \(\phi\) 被优化。

[4]:

fit1 = Holt(air, initialization_method="estimated").fit(
    smoothing_level=0.8, smoothing_trend=0.2, optimized=False
)
fcast1 = fit1.forecast(5).rename("Holt's linear trend")
fit2 = Holt(air, exponential=True, initialization_method="estimated").fit(
    smoothing_level=0.8, smoothing_trend=0.2, optimized=False
)
fcast2 = fit2.forecast(5).rename("Exponential trend")
fit3 = Holt(air, damped_trend=True, initialization_method="estimated").fit(
    smoothing_level=0.8, smoothing_trend=0.2
)
fcast3 = fit3.forecast(5).rename("Additive damped trend")

plt.figure(figsize=(12, 8))
plt.plot(air, marker="o", color="black")
plt.plot(fit1.fittedvalues, color="blue")
(line1,) = plt.plot(fcast1, marker="o", color="blue")
plt.plot(fit2.fittedvalues, color="red")
(line2,) = plt.plot(fcast2, marker="o", color="red")
plt.plot(fit3.fittedvalues, color="green")
(line3,) = plt.plot(fcast3, marker="o", color="green")
plt.legend([line1, line2, line3], [fcast1.name, fcast2.name, fcast3.name])

[4]:

<matplotlib.legend.Legend at 0x7f4b3c76be20>
../../../_images/examples_notebooks_generated_exponential_smoothing_8_1.png

季节性调整数据

让我们看看一些季节性调整的牲畜数据。我们拟合了五个霍尔特模型。下面的表格允许我们比较当我们使用指数与加法以及阻尼与非阻尼时得到的结果。

注意：fit4 通过提供 \(\phi=0.98\) 的固定值，不允许参数 \(\phi\) 被优化。

[5]:

fit1 = SimpleExpSmoothing(livestock2, initialization_method="estimated").fit()
fit2 = Holt(livestock2, initialization_method="estimated").fit()
fit3 = Holt(livestock2, exponential=True, initialization_method="estimated").fit()
fit4 = Holt(livestock2, damped_trend=True, initialization_method="estimated").fit(
    damping_trend=0.98
)
fit5 = Holt(
    livestock2, exponential=True, damped_trend=True, initialization_method="estimated"
).fit()
params = [
    "smoothing_level",
    "smoothing_trend",
    "damping_trend",
    "initial_level",
    "initial_trend",
]
results = pd.DataFrame(
    index=[r"$\alpha$", r"$\beta$", r"$\phi$", r"$l_0$", "$b_0$", "SSE"],
    columns=["SES", "Holt's", "Exponential", "Additive", "Multiplicative"],
)
results["SES"] = [fit1.params[p] for p in params] + [fit1.sse]
results["Holt's"] = [fit2.params[p] for p in params] + [fit2.sse]
results["Exponential"] = [fit3.params[p] for p in params] + [fit3.sse]
results["Additive"] = [fit4.params[p] for p in params] + [fit4.sse]
results["Multiplicative"] = [fit5.params[p] for p in params] + [fit5.sse]
results

[5]:
SES 霍尔特 指数 加法 乘法
$\alpha$ 1.000000 0.974338 0.977642 0.978843 0.974912
$\beta$ NaN 0.000000 0.000000 0.000008 0.000000
$\phi$ NaN NaN NaN 0.980000 0.981646
$l_0$ 263.917703 258.882683 260.335599 257.357716 258.951817
$b_0$ NaN 5.010856 1.013780 6.645297 1.038144
SSE 6761.350235 6004.138207 6104.194782 6036.597169 6081.995045

季节性调整数据的图

以下图表允许我们评估上述表格中拟合的水平和斜率/趋势分量。

[6]:

for fit in [fit2, fit4]:
    pd.DataFrame(np.c_[fit.level, fit.trend]).rename(
        columns={0: "level", 1: "slope"}
    ).plot(subplots=True)
plt.show()
print(
    "Figure 7.4: Level and slope components for Holt’s linear trend method and the additive damped trend method."
)
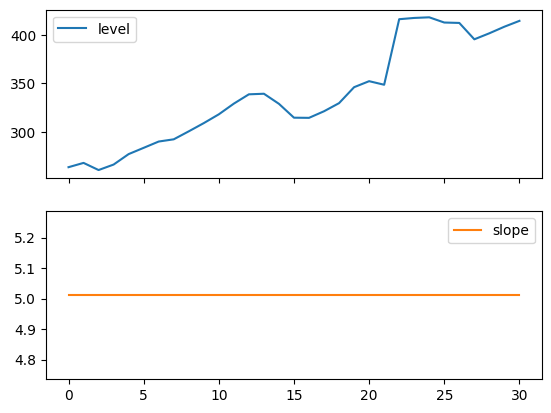
../../../_images/examples_notebooks_generated_exponential_smoothing_12_0.png
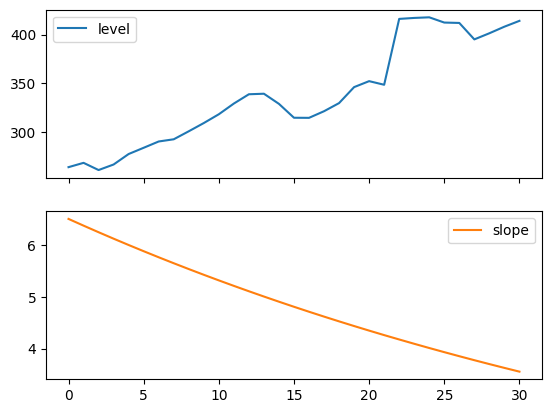
../../../_images/examples_notebooks_generated_exponential_smoothing_12_1.png 
Figure 7.4: Level and slope components for Holt’s linear trend method and the additive damped trend method.

比较

在这里，我们绘制了简单指数平滑和霍尔特方法的比较，包括各种加法、指数和阻尼组合。所有模型参数将由 statsmodels 优化。

[7]:

fit1 = SimpleExpSmoothing(livestock2, initialization_method="estimated").fit()
fcast1 = fit1.forecast(9).rename("SES")
fit2 = Holt(livestock2, initialization_method="estimated").fit()
fcast2 = fit2.forecast(9).rename("Holt's")
fit3 = Holt(livestock2, exponential=True, initialization_method="estimated").fit()
fcast3 = fit3.forecast(9).rename("Exponential")
fit4 = Holt(livestock2, damped_trend=True, initialization_method="estimated").fit(
    damping_trend=0.98
)
fcast4 = fit4.forecast(9).rename("Additive Damped")
fit5 = Holt(
    livestock2, exponential=True, damped_trend=True, initialization_method="estimated"
).fit()
fcast5 = fit5.forecast(9).rename("Multiplicative Damped")

ax = livestock2.plot(color="black", marker="o", figsize=(12, 8))
livestock3.plot(ax=ax, color="black", marker="o", legend=False)
fcast1.plot(ax=ax, color="red", legend=True)
fcast2.plot(ax=ax, color="green", legend=True)
fcast3.plot(ax=ax, color="blue", legend=True)
fcast4.plot(ax=ax, color="cyan", legend=True)
fcast5.plot(ax=ax, color="magenta", legend=True)
ax.set_ylabel("Livestock, sheep in Asia (millions)")
plt.show()
print(
    "Figure 7.5: Forecasting livestock, sheep in Asia: comparing forecasting performance of non-seasonal methods."
)
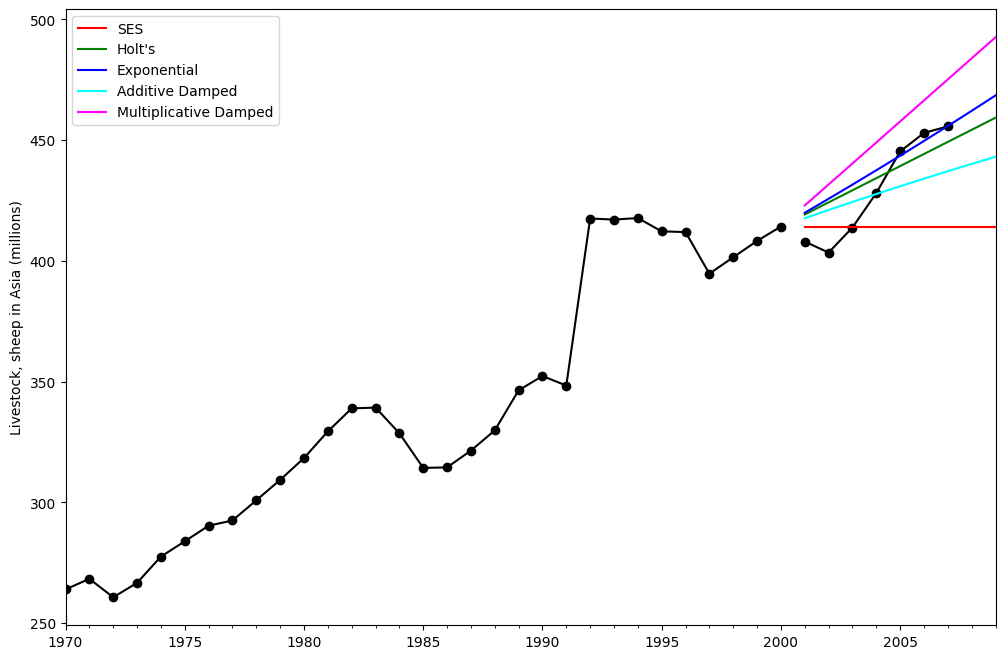
../../../_images/examples_notebooks_generated_exponential_smoothing_14_0.png 
Figure 7.5: Forecasting livestock, sheep in Asia: comparing forecasting performance of non-seasonal methods.

霍尔特-温特斯季节性

最后，我们能够运行完整的霍尔特-温特斯季节性指数平滑，包括趋势分量和季节性分量。statsmodels 允许所有组合，如以下示例所示：1. fit1 加法趋势、周期为 season_length=4 的加法季节性，以及使用 Box-Cox 变换。 1. fit2 加法趋势、周期为 season_length=4 的乘法季节性，以及使用 Box-Cox 变换。 1. fit3 加法阻尼趋势、周期为 season_length=4 的加法季节性，以及使用 Box-Cox 变换。 1. fit4 加法阻尼趋势、周期为 season_length=4 的乘法季节性，以及使用 Box-Cox 变换。

该图显示了 fit1 和 fit2 的结果和预测。表格允许我们比较结果和参数化。

[8]:

fit1 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="add",
    use_boxcox=True,
    initialization_method="estimated",
).fit()
fit2 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    use_boxcox=True,
    initialization_method="estimated",
).fit()
fit3 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="add",
    damped_trend=True,
    use_boxcox=True,
    initialization_method="estimated",
).fit()
fit4 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    damped_trend=True,
    use_boxcox=True,
    initialization_method="estimated",
).fit()
results = pd.DataFrame(
    index=[r"$\alpha$", r"$\beta$", r"$\phi$", r"$\gamma$", r"$l_0$", "$b_0$", "SSE"]
)
params = [
    "smoothing_level",
    "smoothing_trend",
    "damping_trend",
    "smoothing_seasonal",
    "initial_level",
    "initial_trend",
]
results["Additive"] = [fit1.params[p] for p in params] + [fit1.sse]
results["Multiplicative"] = [fit2.params[p] for p in params] + [fit2.sse]
results["Additive Dam"] = [fit3.params[p] for p in params] + [fit3.sse]
results["Multiplica Dam"] = [fit4.params[p] for p in params] + [fit4.sse]

ax = aust.plot(
    figsize=(10, 6),
    marker="o",
    color="black",
    title="Forecasts from Holt-Winters' multiplicative method",
)
ax.set_ylabel("International visitor night in Australia (millions)")
ax.set_xlabel("Year")
fit1.fittedvalues.plot(ax=ax, style="--", color="red")
fit2.fittedvalues.plot(ax=ax, style="--", color="green")

fit1.forecast(8).rename("Holt-Winters (add-add-seasonal)").plot(
    ax=ax, style="--", marker="o", color="red", legend=True
)
fit2.forecast(8).rename("Holt-Winters (add-mul-seasonal)").plot(
    ax=ax, style="--", marker="o", color="green", legend=True
)

plt.show()
print(
    "Figure 7.6: Forecasting international visitor nights in Australia using Holt-Winters method with both additive and multiplicative seasonality."
)

results
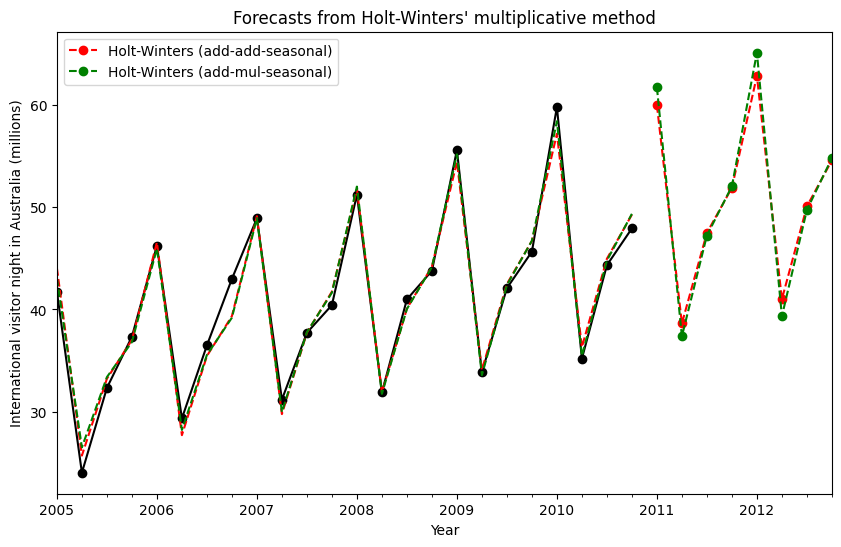
../../../_images/examples_notebooks_generated_exponential_smoothing_16_0.png 
Figure 7.6: Forecasting international visitor nights in Australia using Holt-Winters method with both additive and multiplicative seasonality.

[8]:
加法 乘法 加法 Dam 乘法 Dam
$\alpha$ 1.490116e-08 1.490116e-08 1.490116e-08 1.490116e-08
$\beta$ 1.409865e-08 0.000000e+00 6.490845e-09 5.042120e-09
$\phi$ NaN NaN 9.430416e-01 9.536043e-01
$\gamma$ 7.066690e-16 1.514304e-16 1.169213e-15 0.000000e+00
$l_0$ 1.119348e+01 1.106382e+01 1.084022e+01 9.899305e+00
$b_0$ 1.205396e-01 1.198963e-01 2.456750e-01 1.975449e-01
SSE 4.402746e+01 3.611262e+01 3.527620e+01 3.062033e+01

内部机制

可以获取指数平滑模型的内部机制。

在这里，我们展示了一些表格，允许您并排查看原始值 \(y_t\)、水平 \(l_t\)、趋势 \(b_t\)、季节性 \(s_t\) 以及拟合值 \(\hat{y}_t\)。请注意，如果拟合在没有 Box-Cox 变换的情况下进行，这些值仅在原始数据的空间中具有有意义的值。

[9]:

fit1 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="add",
    initialization_method="estimated",
).fit()
fit2 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    initialization_method="estimated",
).fit()

[10]:

df = pd.DataFrame(
    np.c_[aust, fit1.level, fit1.trend, fit1.season, fit1.fittedvalues],
    columns=[r"$y_t$", r"$l_t$", r"$b_t$", r"$s_t$", r"$\hat{y}_t$"],
    index=aust.index,
)
forecasts = fit1.forecast(8).rename(r"$\hat{y}_t$").to_frame()
df = pd.concat([df, forecasts], axis=0, sort=True)

[11]:

df = pd.DataFrame(
    np.c_[aust, fit2.level, fit2.trend, fit2.season, fit2.fittedvalues],
    columns=[r"$y_t$", r"$l_t$", r"$b_t$", r"$s_t$", r"$\hat{y}_t$"],
    index=aust.index,
)
forecasts = fit2.forecast(8).rename(r"$\hat{y}_t$").to_frame()
df = pd.concat([df, forecasts], axis=0, sort=True)

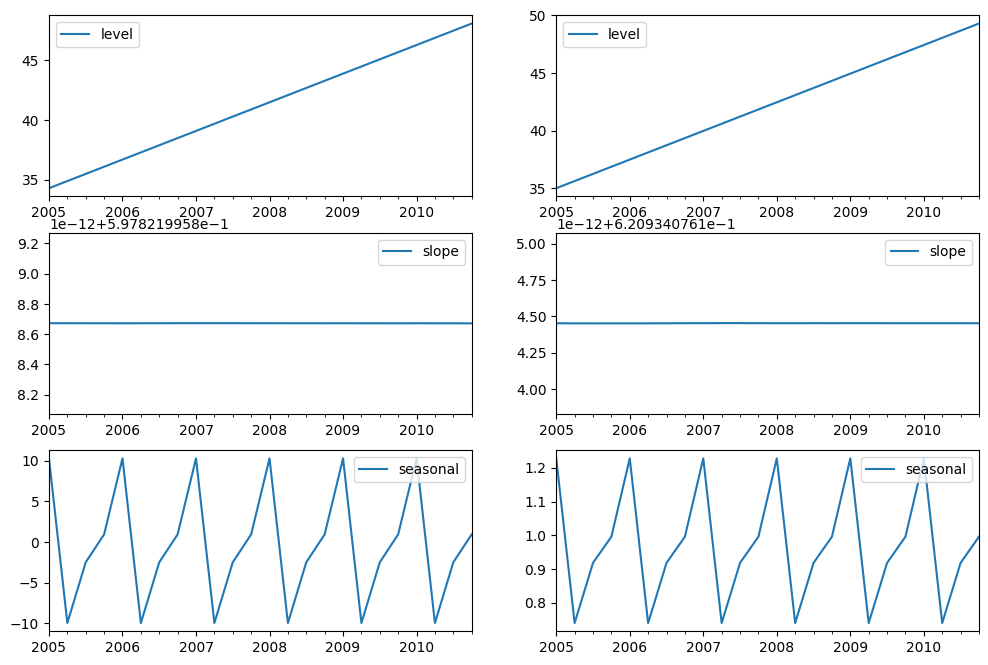
最后，让我们看一下模型的水平、斜率/趋势和季节性分量。

[12]:

states1 = pd.DataFrame(
    np.c_[fit1.level, fit1.trend, fit1.season],
    columns=["level", "slope", "seasonal"],
    index=aust.index,
)
states2 = pd.DataFrame(
    np.c_[fit2.level, fit2.trend, fit2.season],
    columns=["level", "slope", "seasonal"],
    index=aust.index,
)
fig, [[ax1, ax4], [ax2, ax5], [ax3, ax6]] = plt.subplots(3, 2, figsize=(12, 8))
states1[["level"]].plot(ax=ax1)
states1[["slope"]].plot(ax=ax2)
states1[["seasonal"]].plot(ax=ax3)
states2[["level"]].plot(ax=ax4)
states2[["slope"]].plot(ax=ax5)
states2[["seasonal"]].plot(ax=ax6)
plt.show()
../../../_images/examples_notebooks_generated_exponential_smoothing_22_0.png

模拟和置信区间

通过使用状态空间公式，我们可以对未来值进行模拟。数学细节在 Hyndman 和 Athanasopoulos [2] 以及 HoltWintersResults.simulate 的文档中描述。

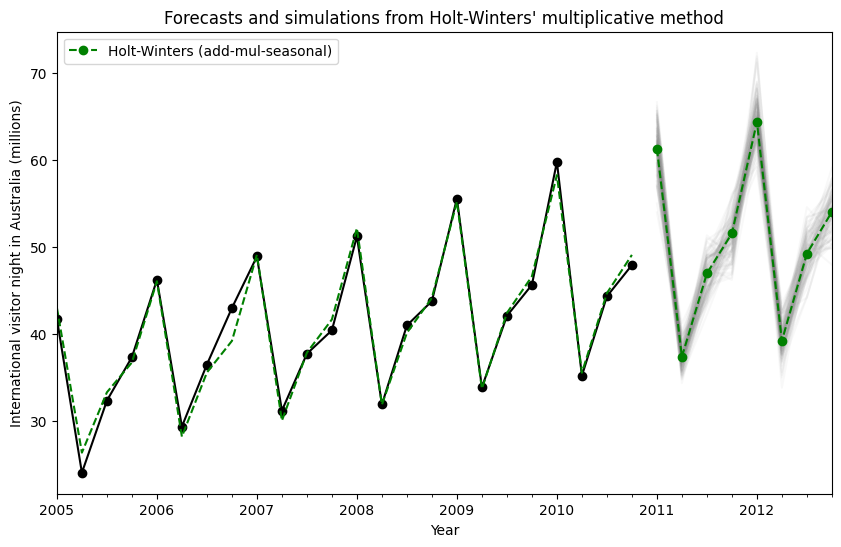
与 [2] 中的示例类似，我们使用具有加法趋势、乘法季节性和乘法误差的模型。我们对未来最多 8 个步骤进行模拟，并执行 1000 次模拟。正如下面图中所示，模拟与预测值非常匹配。

[2] Hyndman, Rob J. 和 George Athanasopoulos。预测：原理与实践，第二版。OTexts，2018 年。

[13]:

fit = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    initialization_method="estimated",
).fit()
simulations = fit.simulate(8, repetitions=100, error="mul")

ax = aust.plot(
    figsize=(10, 6),
    marker="o",
    color="black",
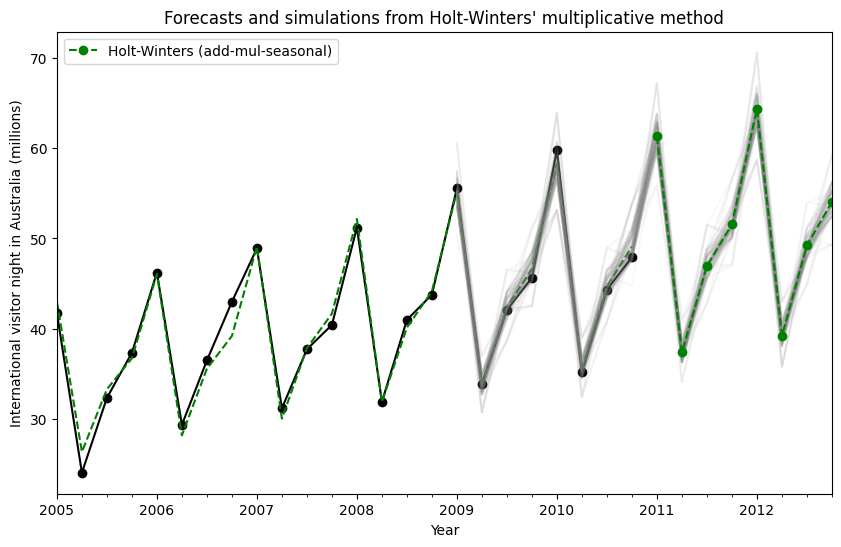
    title="Forecasts and simulations from Holt-Winters' multiplicative method",
)
ax.set_ylabel("International visitor night in Australia (millions)")
ax.set_xlabel("Year")
fit.fittedvalues.plot(ax=ax, style="--", color="green")
simulations.plot(ax=ax, style="-", alpha=0.05, color="grey", legend=False)
fit.forecast(8).rename("Holt-Winters (add-mul-seasonal)").plot(
    ax=ax, style="--", marker="o", color="green", legend=True
)
plt.show()
../../../_images/examples_notebooks_generated_exponential_smoothing_24_0.png

模拟也可以从不同的时间点开始，并且有多种选择随机噪声的方法。

[14]:

fit = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    initialization_method="estimated",
).fit()
simulations = fit.simulate(
    16, anchor="2009-01-01", repetitions=100, error="mul", random_errors="bootstrap"
)

ax = aust.plot(
    figsize=(10, 6),
    marker="o",
    color="black",
    title="Forecasts and simulations from Holt-Winters' multiplicative method",
)
ax.set_ylabel("International visitor night in Australia (millions)")
ax.set_xlabel("Year")
fit.fittedvalues.plot(ax=ax, style="--", color="green")
simulations.plot(ax=ax, style="-", alpha=0.05, color="grey", legend=False)
fit.forecast(8).rename("Holt-Winters (add-mul-seasonal)").plot(
    ax=ax, style="--", marker="o", color="green", legend=True
)
plt.show()
../../../_images/examples_notebooks_generated_exponential_smoothing_26_0.png
上次更新：2024 年 10 月 3 日