马尔可夫切换动态回归模型

此笔记本提供了一个使用 statsmodels 中马尔可夫切换模型的示例，用于估计具有状态变化的动态回归模型。它遵循 Stata 马尔可夫切换文档中的示例，该文档可在 http://www.stata.com/manuals14/tsmswitch.pdf 中找到。

[1]:

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# NBER recessions
from pandas_datareader.data import DataReader
from datetime import datetime

usrec = DataReader(
    "USREC", "fred", start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)
)

联邦基金利率与切换截距

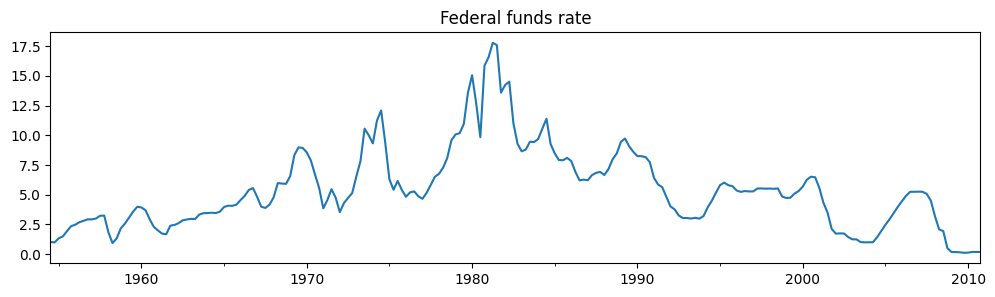
第一个示例将联邦基金利率建模为围绕一个常数截距的噪声，但截距在不同的状态期间发生变化。该模型很简单

\[r_t = \mu_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]

其中 \(S_t \in \{0, 1\}\)，状态转换根据以下公式进行

\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]

我们将通过最大似然估计该模型的参数：\(p_{00}, p_{10}, \mu_0, \mu_1, \sigma^2\)。

此示例中使用的数据可在 https://www.stata-press.com/data/r14/usmacro 中找到。

[2]:

# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import fedfunds

dta_fedfunds = pd.Series(
    fedfunds, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS")
)

# Plot the data
dta_fedfunds.plot(title="Federal funds rate", figsize=(12, 3))

# Fit the model
# (a switching mean is the default of the MarkovRegession model)
mod_fedfunds = sm.tsa.MarkovRegression(dta_fedfunds, k_regimes=2)
res_fedfunds = mod_fedfunds.fit()
../../../_images/examples_notebooks_generated_markov_regression_4_0.png 
[3]:

res_fedfunds.summary()

[3]:
马尔可夫切换模型结果
因变量 y 观测次数 226
模型 MarkovRegression 对数似然 -508.636
日期 Thu, 03 Oct 2024 AIC 1027.272
时间 15:45:37 BIC 1044.375
样本 07-01-1954 HQIC 1034.174
- 10-01-2010
协方差类型 approx
状态 0 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 3.7088 0.177 20.988 0.000 3.362 4.055
状态 1 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 9.5568 0.300 31.857 0.000 8.969 10.145
非切换参数
系数 标准误 z P>|z| [0.025 0.975]
sigma2 4.4418 0.425 10.447 0.000 3.608 5.275
状态转换参数
系数 标准误 z P>|z| [0.025 0.975]
p[0->0] 0.9821 0.010 94.443 0.000 0.962 1.002
p[1->0] 0.0504 0.027 1.876 0.061 -0.002 0.103


警告
[1] 使用数值（复数步）微分计算的协方差矩阵。

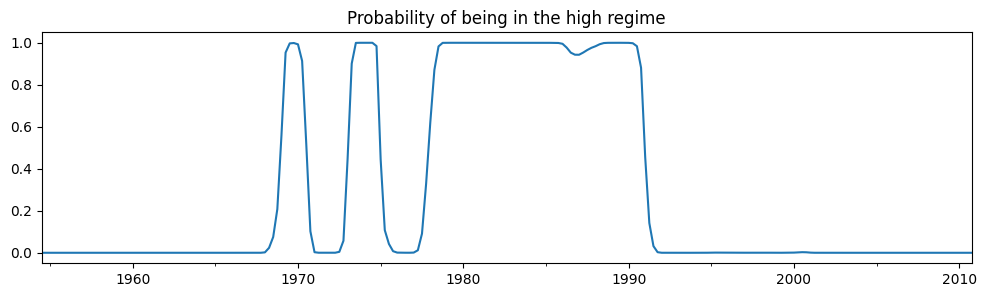
从摘要输出中，第一个状态（“低状态”）中的平均联邦基金利率估计为 \(3.7\)，而“高状态”中的平均联邦基金利率估计为 \(9.6\)。下面我们绘制处于高状态的平滑概率。该模型表明 1980 年代是一个联邦基金利率处于高位的时期。

[4]:

res_fedfunds.smoothed_marginal_probabilities[1].plot(
    title="Probability of being in the high regime", figsize=(12, 3)
)

[4]:

<Axes: title={'center': 'Probability of being in the high regime'}>
../../../_images/examples_notebooks_generated_markov_regression_7_1.png

从估计的转换矩阵中，我们可以计算出低状态和高状态的预期持续时间。

[5]:

print(res_fedfunds.expected_durations)

[55.85400626 19.85506546]

低状态预计会持续约 14 年，而高状态预计只会持续约 5 年。

联邦基金利率与切换截距和滞后因变量

第二个示例扩展了之前的模型，以包括联邦基金利率的滞后值。

\[r_t = \mu_{S_t} + r_{t-1} \beta_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]

其中 \(S_t \in \{0, 1\}\)，状态转换根据以下公式进行

\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]

我们将通过最大似然估计该模型的参数：\(p_{00}, p_{10}, \mu_0, \mu_1, \beta_0, \beta_1, \sigma^2\)。

[6]:

# Fit the model
mod_fedfunds2 = sm.tsa.MarkovRegression(
    dta_fedfunds.iloc[1:], k_regimes=2, exog=dta_fedfunds.iloc[:-1]
)
res_fedfunds2 = mod_fedfunds2.fit()

[7]:

res_fedfunds2.summary()

[7]:
马尔可夫切换模型结果
因变量 y 观测次数 225
模型 MarkovRegression 对数似然 -264.711
日期 Thu, 03 Oct 2024 AIC 543.421
时间 15:45:38 BIC 567.334
样本 10-01-1954 HQIC 553.073
- 10-01-2010
协方差类型 approx
状态 0 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 0.7245 0.289 2.510 0.012 0.159 1.290
x1 0.7631 0.034 22.629 0.000 0.697 0.829
状态 1 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 -0.0989 0.118 -0.835 0.404 -0.331 0.133
x1 1.0612 0.019 57.351 0.000 1.025 1.097
非切换参数
系数 标准误 z P>|z| [0.025 0.975]
sigma2 0.4783 0.050 9.642 0.000 0.381 0.576
状态转换参数
系数 标准误 z P>|z| [0.025 0.975]
p[0->0] 0.6378 0.120 5.304 0.000 0.402 0.874
p[1->0] 0.1306 0.050 2.634 0.008 0.033 0.228


警告
[1] 使用数值（复数步）微分计算的协方差矩阵。

从摘要输出中可以注意到一些事情

  1. 信息准则大幅下降，表明此模型比之前的模型拟合得更好。

  2. 状态的解释，就截距而言，已经发生了变化。现在，第一个状态具有更高的截距，而第二个状态具有更低的截距。

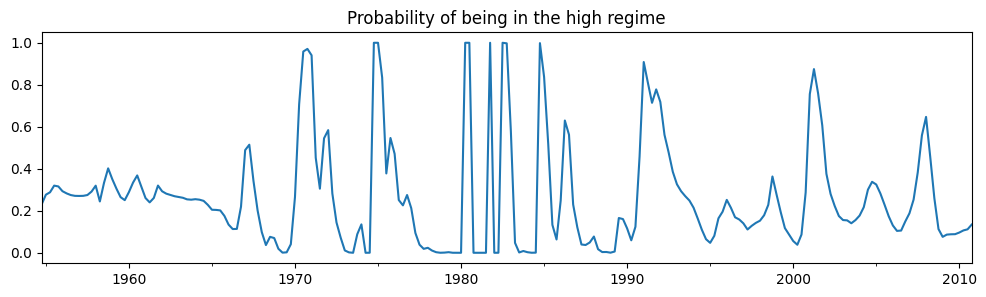
检查高状态的平滑概率，我们现在看到相当多的可变性。

[8]:

res_fedfunds2.smoothed_marginal_probabilities[0].plot(
    title="Probability of being in the high regime", figsize=(12, 3)
)

[8]:

<Axes: title={'center': 'Probability of being in the high regime'}>
../../../_images/examples_notebooks_generated_markov_regression_15_1.png

最后，每个状态的预期持续时间都大大减少。

[9]:

print(res_fedfunds2.expected_durations)

[2.76105188 7.65529154]

泰勒规则与 2 或 3 个状态

我们现在包括了两个额外的外生变量——产出缺口指标和通货膨胀指标——来估计一个具有 2 个和 3 个状态的切换泰勒类型规则，以查看哪一个更适合数据。

由于模型的估计通常很困难，对于 3 状态模型，我们在起始参数上进行搜索以改进结果，指定 20 次随机搜索重复。

[10]:

# Get the additional data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import ogap, inf

dta_ogap = pd.Series(ogap, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS"))
dta_inf = pd.Series(inf, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS"))

exog = pd.concat((dta_fedfunds.shift(), dta_ogap, dta_inf), axis=1).iloc[4:]

# Fit the 2-regime model
mod_fedfunds3 = sm.tsa.MarkovRegression(dta_fedfunds.iloc[4:], k_regimes=2, exog=exog)
res_fedfunds3 = mod_fedfunds3.fit()

# Fit the 3-regime model
np.random.seed(12345)
mod_fedfunds4 = sm.tsa.MarkovRegression(dta_fedfunds.iloc[4:], k_regimes=3, exog=exog)
res_fedfunds4 = mod_fedfunds4.fit(search_reps=20)

[11]:

res_fedfunds3.summary()

[11]:
马尔可夫切换模型结果
因变量 y 观测次数 222
模型 MarkovRegression 对数似然 -229.256
日期 Thu, 03 Oct 2024 AIC 480.512
时间 15:45:42 BIC 517.942
样本 07-01-1955 HQIC 495.624
- 10-01-2010
协方差类型 approx
状态 0 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 0.6555 0.137 4.771 0.000 0.386 0.925
x1 0.8314 0.033 24.951 0.000 0.766 0.897
x2 0.1355 0.029 4.609 0.000 0.078 0.193
x3 -0.0274 0.041 -0.671 0.502 -0.107 0.053
状态 1 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 -0.0945 0.128 -0.739 0.460 -0.345 0.156
x1 0.9293 0.027 34.309 0.000 0.876 0.982
x2 0.0343 0.024 1.429 0.153 -0.013 0.081
x3 0.2125 0.030 7.147 0.000 0.154 0.271
非切换参数
系数 标准误 z P>|z| [0.025 0.975]
sigma2 0.3323 0.035 9.526 0.000 0.264 0.401
状态转换参数
系数 标准误 z P>|z| [0.025 0.975]
p[0->0] 0.7279 0.093 7.828 0.000 0.546 0.910
p[1->0] 0.2115 0.064 3.298 0.001 0.086 0.337


警告
[1] 使用数值（复数步）微分计算的协方差矩阵。
[12]:

res_fedfunds4.summary()

[12]:
马尔可夫切换模型结果
因变量 y 观测次数 222
模型 MarkovRegression 对数似然 -180.806
日期 Thu, 03 Oct 2024 AIC 399.611
时间 15:45:42 BIC 464.262
样本 07-01-1955 HQIC 425.713
- 10-01-2010
协方差类型 approx
状态 0 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 -1.0250 0.290 -3.531 0.000 -1.594 -0.456
x1 0.3277 0.086 3.812 0.000 0.159 0.496
x2 0.2036 0.049 4.152 0.000 0.107 0.300
x3 1.1381 0.081 13.977 0.000 0.978 1.298
状态 1 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 -0.0259 0.087 -0.298 0.765 -0.196 0.144
x1 0.9737 0.019 50.265 0.000 0.936 1.012
x2 0.0341 0.017 2.030 0.042 0.001 0.067
x3 0.1215 0.022 5.606 0.000 0.079 0.164
状态 2 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 0.7346 0.130 5.632 0.000 0.479 0.990
x1 0.8436 0.024 35.198 0.000 0.797 0.891
x2 0.1633 0.025 6.515 0.000 0.114 0.212
x3 -0.0499 0.027 -1.835 0.067 -0.103 0.003
非切换参数
系数 标准误 z P>|z| [0.025 0.975]
sigma2 0.1660 0.018 9.240 0.000 0.131 0.201
状态转换参数
系数 标准误 z P>|z| [0.025 0.975]
p[0->0] 0.7214 0.117 6.177 0.000 0.493 0.950
p[1->0] 4.001e-08 nan nan nan nan nan
p[2->0] 0.0783 0.038 2.079 0.038 0.004 0.152
p[0->1] 0.1044 0.095 1.103 0.270 -0.081 0.290
p[1->1] 0.8259 0.054 15.208 0.000 0.719 0.932
p[2->1] 0.2288 0.073 3.150 0.002 0.086 0.371


警告
[1] 使用数值（复数步）微分计算的协方差矩阵。

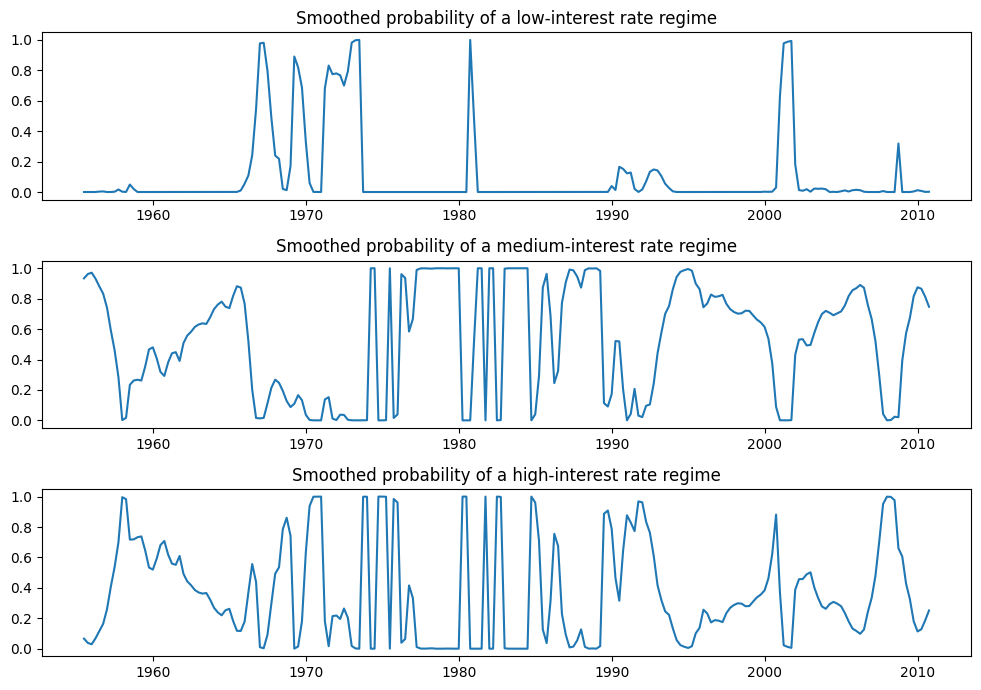
由于信息准则较低，我们可能更喜欢 3 状态模型，其解释为低利率状态、中利率状态和高利率状态。每个状态的平滑概率绘制如下。

[13]:

fig, axes = plt.subplots(3, figsize=(10, 7))

ax = axes[0]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[0])
ax.set(title="Smoothed probability of a low-interest rate regime")

ax = axes[1]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[1])
ax.set(title="Smoothed probability of a medium-interest rate regime")

ax = axes[2]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[2])
ax.set(title="Smoothed probability of a high-interest rate regime")

fig.tight_layout()
../../../_images/examples_notebooks_generated_markov_regression_23_0.png

切换方差

我们还可以适应切换方差。特别地，我们考虑模型

\[y_t = \mu_{S_t} + y_{t-1} \beta_{S_t} + \varepsilon_t \quad \varepsilon_t \sim N(0, \sigma_{S_t}^2)\]

我们使用最大似然估计该模型的参数：\(p_{00}, p_{10}, \mu_0, \mu_1, \beta_0, \beta_1, \sigma_0^2, \sigma_1^2\)。

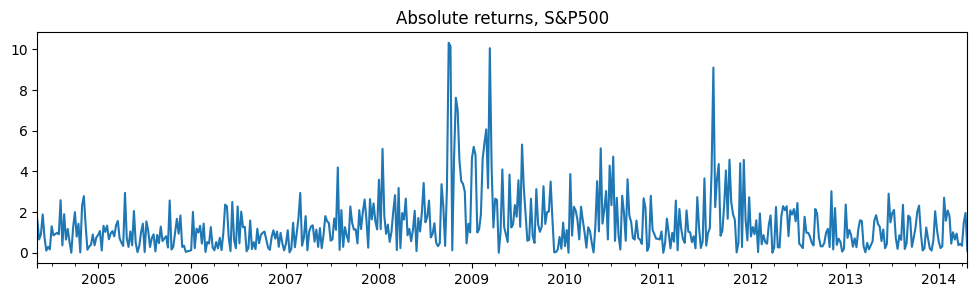
该应用针对股票的绝对收益率，数据可在 https://www.stata-press.com/data/r14/snp500 中找到。

[14]:

# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import areturns

dta_areturns = pd.Series(
    areturns, index=pd.date_range("2004-05-04", "2014-5-03", freq="W")
)

# Plot the data
dta_areturns.plot(title="Absolute returns, S&P500", figsize=(12, 3))

# Fit the model
mod_areturns = sm.tsa.MarkovRegression(
    dta_areturns.iloc[1:],
    k_regimes=2,
    exog=dta_areturns.iloc[:-1],
    switching_variance=True,
)
res_areturns = mod_areturns.fit()
../../../_images/examples_notebooks_generated_markov_regression_25_0.png 
[15]:

res_areturns.summary()

[15]:
马尔可夫切换模型结果
因变量 y 观测次数 520
模型 MarkovRegression 对数似然 -745.798
日期 Thu, 03 Oct 2024 AIC 1507.595
时间 15:45:44 BIC 1541.626
样本 05-16-2004 HQIC 1520.926
- 04-27-2014
协方差类型 approx
状态 0 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 0.7641 0.078 9.761 0.000 0.611 0.918
x1 0.0791 0.030 2.620 0.009 0.020 0.138
sigma2 0.3476 0.061 5.694 0.000 0.228 0.467
状态 1 参数
系数 标准误 z P>|z| [0.025 0.975]
常数 1.9728 0.278 7.086 0.000 1.427 2.518
x1 0.5280 0.086 6.155 0.000 0.360 0.696
sigma2 2.5771 0.405 6.357 0.000 1.783 3.372
状态转换参数
系数 标准误 z P>|z| [0.025 0.975]
p[0->0] 0.7531 0.063 11.871 0.000 0.629 0.877
p[1->0] 0.6825 0.066 10.301 0.000 0.553 0.812


警告
[1] 使用数值（复数步）微分计算的协方差矩阵。

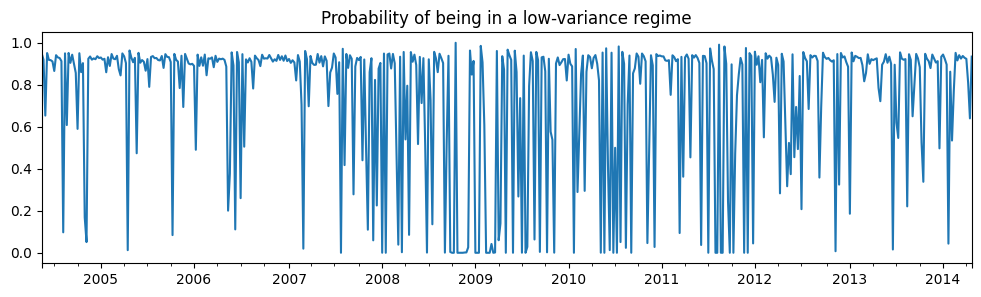
第一个状态是低方差状态，第二个状态是高方差状态。下面我们绘制处于低方差状态的概率。在 2008 年至 2012 年之间，似乎没有明显的迹象表明有一个状态引导经济发展。

[16]:

res_areturns.smoothed_marginal_probabilities[0].plot(
    title="Probability of being in a low-variance regime", figsize=(12, 3)
)

[16]:

<Axes: title={'center': 'Probability of being in a low-variance regime'}>
../../../_images/examples_notebooks_generated_markov_regression_28_1.png
上次更新：2024 年 10 月 3 日