使用 LOESS 的多重季节趋势分解 (MSTL)¶

此笔记本说明了如何使用 MSTL [1] 将时间序列分解为：趋势成分、多个季节成分和残差成分。MSTL 使用 STL（使用 LOESS 的季节趋势分解）来迭代地从时间序列中提取季节成分。输入 MSTL 的关键参数是

periods - 每个季节成分的周期（例如，对于具有每日和每周季节性的每小时数据，我们将有：periods=(24, 24*7)。
windows - 每个季节平滑器相对于每个周期的长度。如果这些长度很大，那么季节成分将显示出较少的时变性。必须是奇数。如果为 None，则使用原始论文 [1] 中的实验确定的默认值集。
lmbda - 分解之前进行 Box-Cox 变换的 lambda 参数。如果为 None，则不进行变换。如果为 "auto"，则从数据中自动选择一个合适的 lambda 值。
iterate - 用于细化季节成分的迭代次数。
stl_kwargs - 可以传递给 STL 的所有其他参数（例如，robust、seasonal_deg 等）。请参阅 STL 文档.

[1] K. Bandura、R.J. Hyndman 和 C. Bergmeir (2021) MSTL：一种用于具有多个季节模式的时间序列的季节趋势分解算法。arXiv 预印本 arXiv:2107.13462。

请注意，此实现与 1 中存在一些关键区别。必须在 MSTL 类之外处理缺失数据。论文中提出的算法处理了不存在季节性的情况。此实现假设至少存在一个季节成分。

首先，我们导入所需的包、准备图形环境并准备数据。

[1]:

import matplotlib.pyplot as plt
import datetime
import pandas as pd
import numpy as np
import seaborn as sns
from pandas.plotting import register_matplotlib_converters

from statsmodels.tsa.seasonal import MSTL
from statsmodels.tsa.seasonal import DecomposeResult

register_matplotlib_converters()
sns.set_style("darkgrid")

[2]:

plt.rc("figure", figsize=(16, 12))
plt.rc("font", size=13)

MSTL 应用于玩具数据集¶

创建具有多个季节性的玩具数据集¶

我们创建一个具有每小时频率的时间序列，该时间序列具有遵循正弦波的每日和每周季节性。我们将在笔记本的后面演示一个更现实的示例。

[3]:

t = np.arange(1, 1000)
daily_seasonality = 5 * np.sin(2 * np.pi * t / 24)
weekly_seasonality = 10 * np.sin(2 * np.pi * t / (24 * 7))
trend = 0.0001 * t**2
y = trend + daily_seasonality + weekly_seasonality + np.random.randn(len(t))
ts = pd.date_range(start="2020-01-01", freq="H", periods=len(t))
df = pd.DataFrame(data=y, index=ts, columns=["y"])

/tmp/ipykernel_5245/288299940.py:6: FutureWarning: 'H' is deprecated and will be removed in a future version, please use 'h' instead.
  ts = pd.date_range(start="2020-01-01", freq="H", periods=len(t))

[4]:

df.head()

[4]:

	y
2020-01-01 00:00:00	2.430365
2020-01-01 01:00:00	1.790566
2020-01-01 02:00:00	4.625017
2020-01-01 03:00:00	7.025365
2020-01-01 04:00:00	7.388021

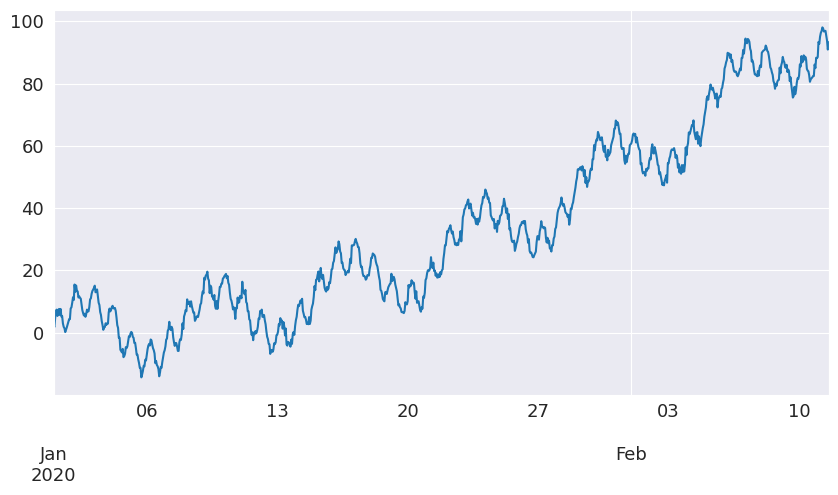
让我们绘制时间序列

[5]:

df["y"].plot(figsize=[10, 5])

[5]:

<Axes: >

../../../_images/examples_notebooks_generated_mstl_decomposition_9_1.png

使用 MSTL 分解玩具数据集¶

让我们使用 MSTL 将时间序列分解为趋势成分、每日和每周季节成分以及残差成分。

[6]:

mstl = MSTL(df["y"], periods=[24, 24 * 7])
res = mstl.fit()

如果输入是 pandas 数据框，那么季节成分的输出将是一个数据框。每个成分的周期反映在列名中。

[7]:

res.seasonal.head()

[7]:

	seasonal_24	seasonal_168
2020-01-01 00:00:00	1.500231	1.796102
2020-01-01 01:00:00	2.339523	0.227047
2020-01-01 02:00:00	2.736665	2.076791
2020-01-01 03:00:00	5.812639	1.220039
2020-01-01 04:00:00	4.672422	3.259005

[8]:

ax = res.plot()

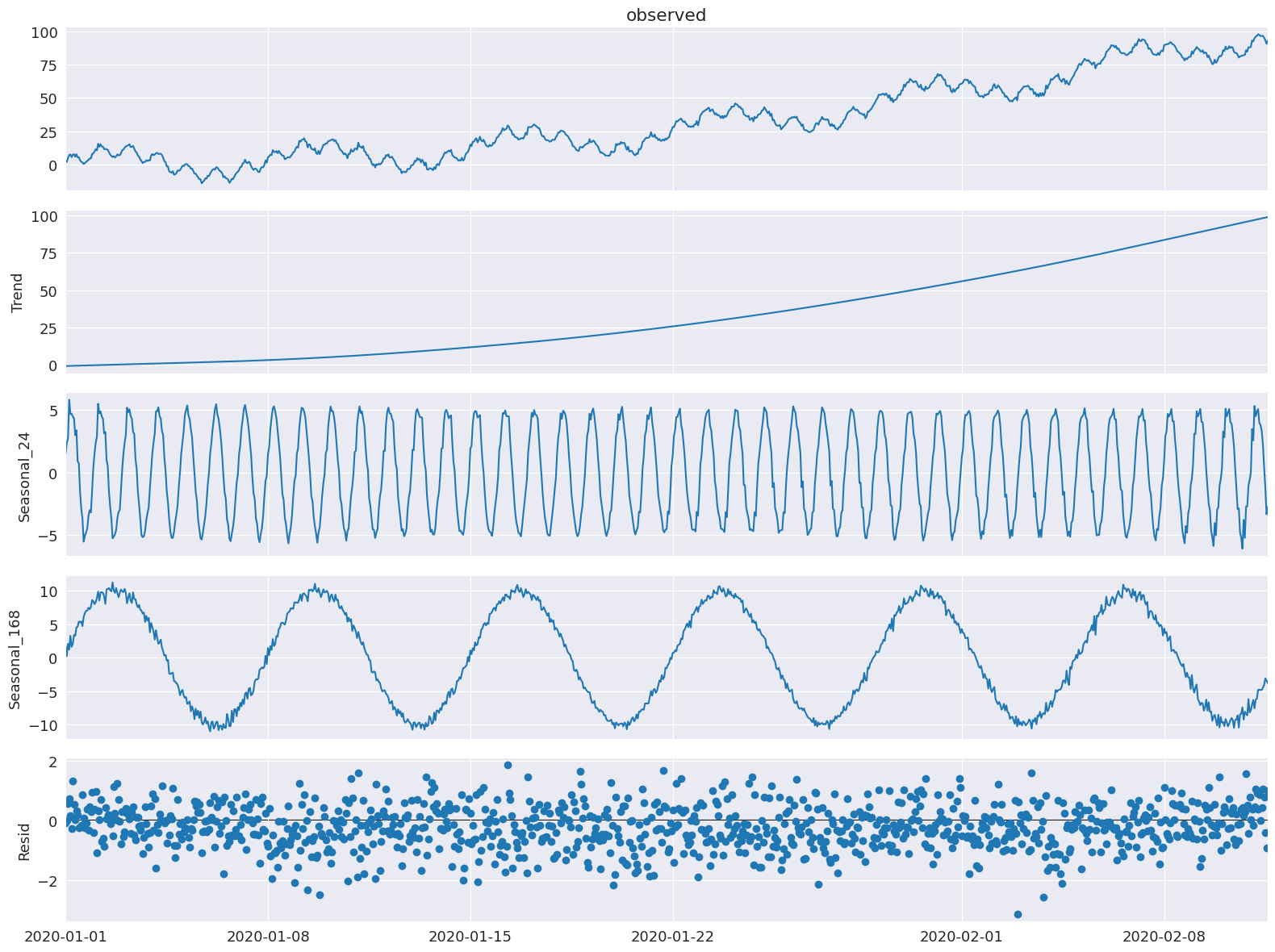
../../../_images/examples_notebooks_generated_mstl_decomposition_15_0.png

我们看到每小时和每周季节成分已经被提取出来。

除了 period 和 seasonal（因为它们在 MSTL 中由 periods 和 windows 设置）之外，所有其他 STL 参数都可以通过将 arg:value 对作为字典传递给 stl_kwargs 来设置（我们现在将展示一个示例）。

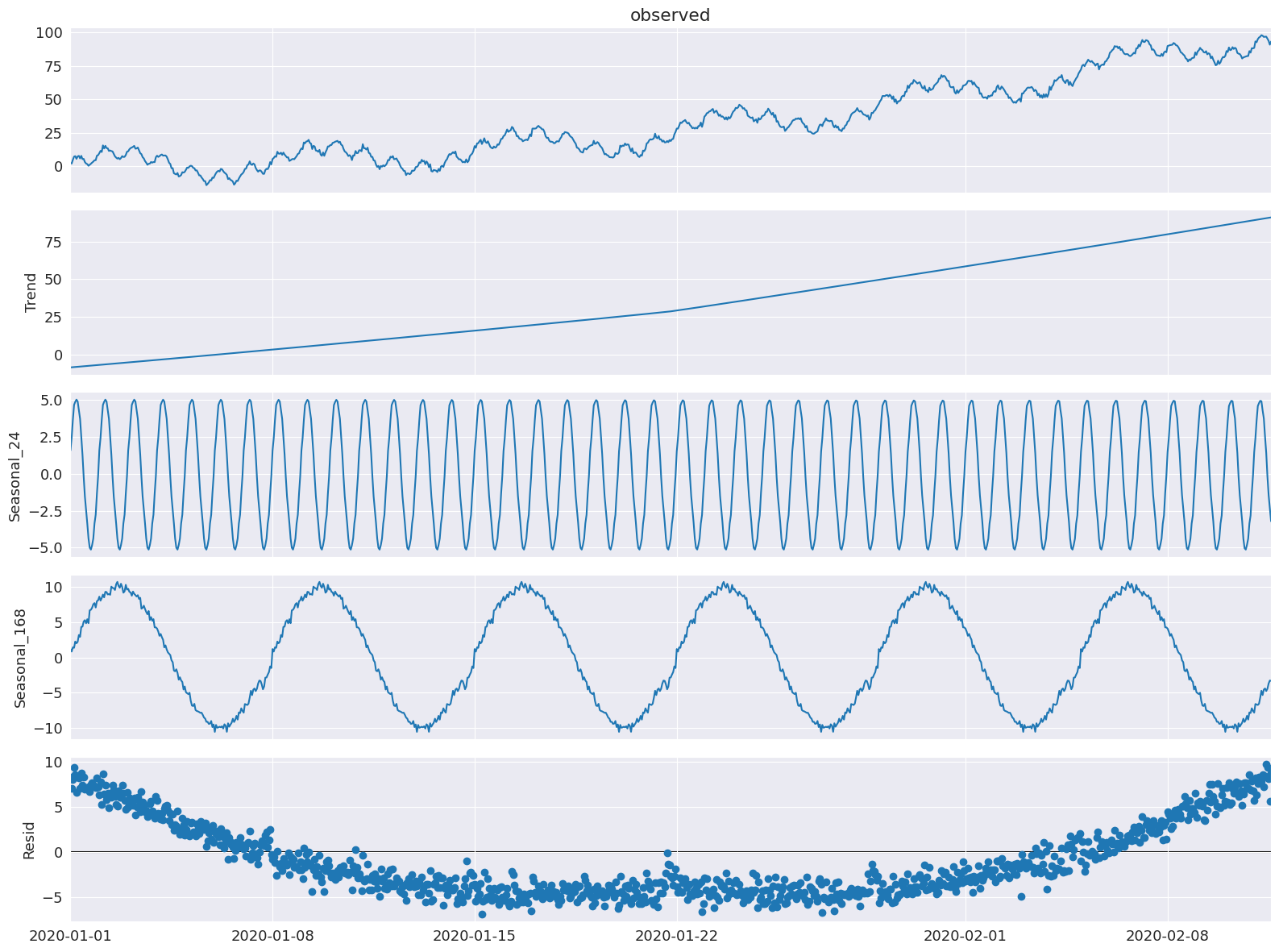
这里我们展示了如何通过 trend 设置 STL 的趋势平滑器，以及通过 seasonal_deg 设置季节拟合的多项式阶数。我们还将显式设置 windows、seasonal_deg 和 iterate 参数。我们将获得更糟糕的拟合，但这只是一个如何将这些参数传递给 MSTL 类的示例。

[9]:

mstl = MSTL(
    df,
    periods=[24, 24 * 7],  # The periods and windows must be the same length and will correspond to one another.
    windows=[101, 101],  # Setting this large along with `seasonal_deg=0` will force the seasonality to be periodic.
    iterate=3,
    stl_kwargs={
                "trend":1001, # Setting this large will force the trend to be smoother.
                "seasonal_deg":0, # Means the seasonal smoother is fit with a moving average.
               }
)
res = mstl.fit()
ax = res.plot()

../../../_images/examples_notebooks_generated_mstl_decomposition_18_0.png

MSTL 应用于电力需求数据集¶

准备数据¶

我们将使用在以下位置找到的维多利亚电力需求数据集：https://github.com/tidyverts/tsibbledata/tree/master/data-raw/vic_elec。此数据集在原始 MSTL 论文 [1] 中使用。这是澳大利亚维多利亚州从 2002 年到 2015 年初的半小时粒度总电力需求。有关数据集的更详细描述，请参见此处。

[10]:

url = "https://raw.githubusercontent.com/tidyverts/tsibbledata/master/data-raw/vic_elec/VIC2015/demand.csv"
df = pd.read_csv(url)

[11]:

df.head()

[11]:

	Date	Period	OperationalLessIndustrial	Industrial
0	37257	1	3535.867064	1086.132936
1	37257	2	3383.499028	1088.500972
2	37257	3	3655.527552	1084.472448
3	37257	4	3510.446636	1085.553364
4	37257	5	3294.697156	1081.302844

日期是表示从原始日期开始的天数的整数。此数据集的原始日期由此处和此处确定，为“1899-12-30”。Period 整数表示 24 小时制中的 30 分钟间隔，因此每天有 48 个间隔。

让我们提取日期和日期时间。

[12]:

df["Date"] = df["Date"].apply(lambda x: pd.Timestamp("1899-12-30") + pd.Timedelta(x, unit="days"))
df["ds"] = df["Date"] + pd.to_timedelta((df["Period"]-1)*30, unit="m")

我们将对 OperationalLessIndustrial 感兴趣，它是不包括某些高能耗工业用户的电力需求。我们将对数据进行每小时重采样，并将数据过滤到与原始 MSTL 论文 [1] 相同的时间段，即 2012 年的前 149 天。

[13]:

timeseries = df[["ds", "OperationalLessIndustrial"]]
timeseries.columns = ["ds", "y"] # Rename to OperationalLessIndustrial to y for simplicity.

# Filter for first 149 days of 2012.
start_date = pd.to_datetime("2012-01-01")
end_date = start_date + pd.Timedelta("149D")
mask = (timeseries["ds"] >= start_date) & (timeseries["ds"] < end_date)
timeseries = timeseries[mask]

# Resample to hourly
timeseries = timeseries.set_index("ds").resample("H").sum()
timeseries.head()

/tmp/ipykernel_5245/185151541.py:11: FutureWarning: 'H' is deprecated and will be removed in a future version, please use 'h' instead.
  timeseries = timeseries.set_index("ds").resample("H").sum()

[13]:

	y
ds
2012-01-01 00:00:00	7926.529376
2012-01-01 01:00:00	7901.826990
2012-01-01 02:00:00	7255.721350
2012-01-01 03:00:00	6792.503352
2012-01-01 04:00:00	6635.984460

使用 MSTL 分解电力需求¶

让我们将 MSTL 应用于此数据集。

注意：stl_kwargs 设置为提供与 [1] 相似的结果，该结果使用 R，因此底层 STL 参数的默认设置略有不同。在实践中，手动设置 inner_iter 和 outer_iter 非常罕见。

[14]:

mstl = MSTL(timeseries["y"], periods=[24, 24 * 7], iterate=3, stl_kwargs={"seasonal_deg": 0,
                                                                          "inner_iter": 2,
                                                                          "outer_iter": 0})
res = mstl.fit() # Use .fit() to perform and return the decomposition
ax = res.plot()
plt.tight_layout()

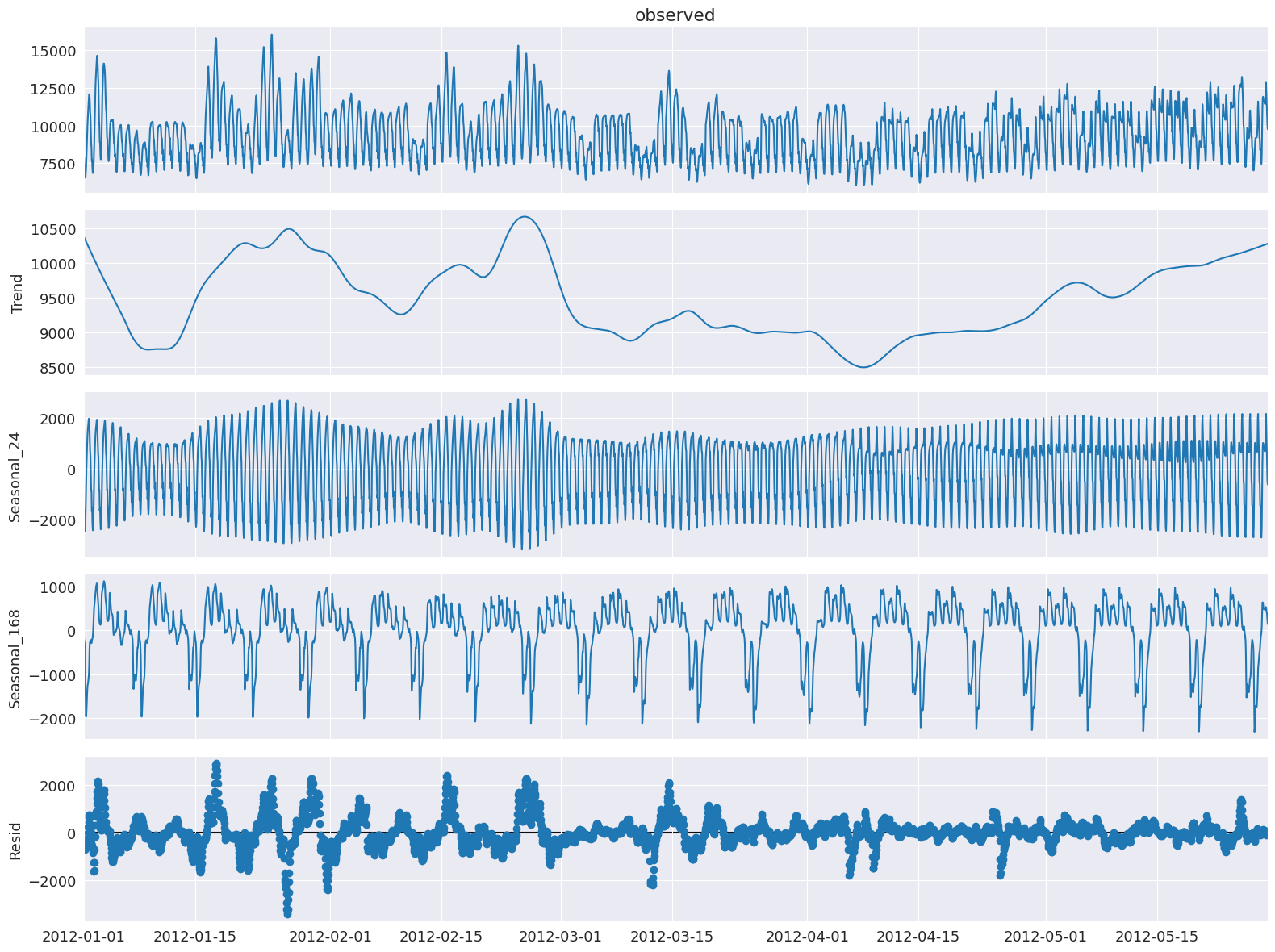
../../../_images/examples_notebooks_generated_mstl_decomposition_30_0.png

多个季节成分存储在 seasonal 属性中，以 pandas 数据框的形式

[15]:

res.seasonal.head()

[15]:

	seasonal_24	seasonal_168
ds
2012-01-01 00:00:00	-1685.986297	-161.807086
2012-01-01 01:00:00	-1591.640845	-229.788887
2012-01-01 02:00:00	-2192.989492	-260.121300
2012-01-01 03:00:00	-2442.169359	-388.484499
2012-01-01 04:00:00	-2357.492551	-660.245476

让我们更详细地检查一下季节成分，并查看前几天和几周，以检查每日和每周季节性。

[16]:

fig, ax = plt.subplots(nrows=2, figsize=[10,10])
res.seasonal["seasonal_24"].iloc[:24*3].plot(ax=ax[0])
ax[0].set_ylabel("seasonal_24")
ax[0].set_title("Daily seasonality")

res.seasonal["seasonal_168"].iloc[:24*7*3].plot(ax=ax[1])
ax[1].set_ylabel("seasonal_168")
ax[1].set_title("Weekly seasonality")

plt.tight_layout()

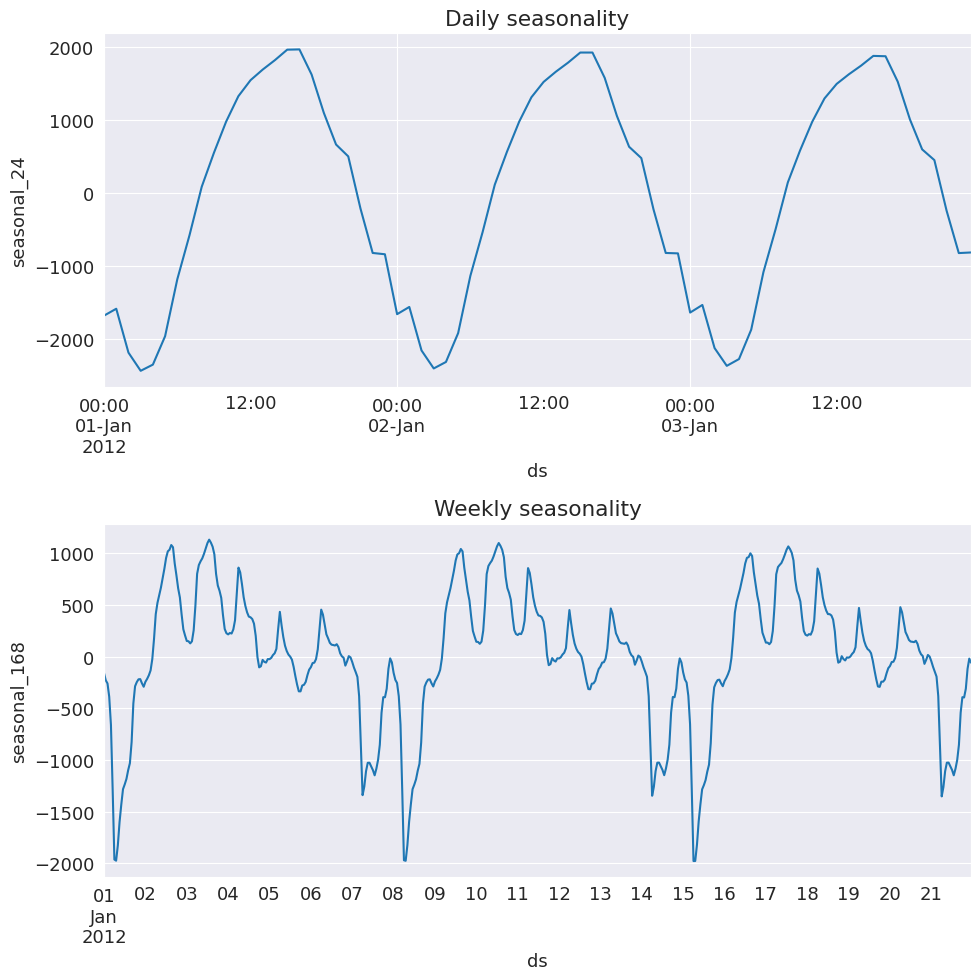
../../../_images/examples_notebooks_generated_mstl_decomposition_34_0.png

我们可以看到电力需求的每日季节性得到了很好的捕捉。这是 1 月份的头几天，所以是在澳大利亚的夏季，下午通常会有一个峰值，这很可能是由于空调的使用造成的。

对于每周季节性，我们可以看到周末期间的需求量较少。

MSTL 的优点之一是它允许我们捕捉到随着时间推移而变化的季节性。因此，让我们看看 5 月份较冷月份的季节性。

[17]:

fig, ax = plt.subplots(nrows=2, figsize=[10,10])
mask = res.seasonal.index.month==5
res.seasonal[mask]["seasonal_24"].iloc[:24*3].plot(ax=ax[0])
ax[0].set_ylabel("seasonal_24")
ax[0].set_title("Daily seasonality")

res.seasonal[mask]["seasonal_168"].iloc[:24*7*3].plot(ax=ax[1])
ax[1].set_ylabel("seasonal_168")
ax[1].set_title("Weekly seasonality")

plt.tight_layout()

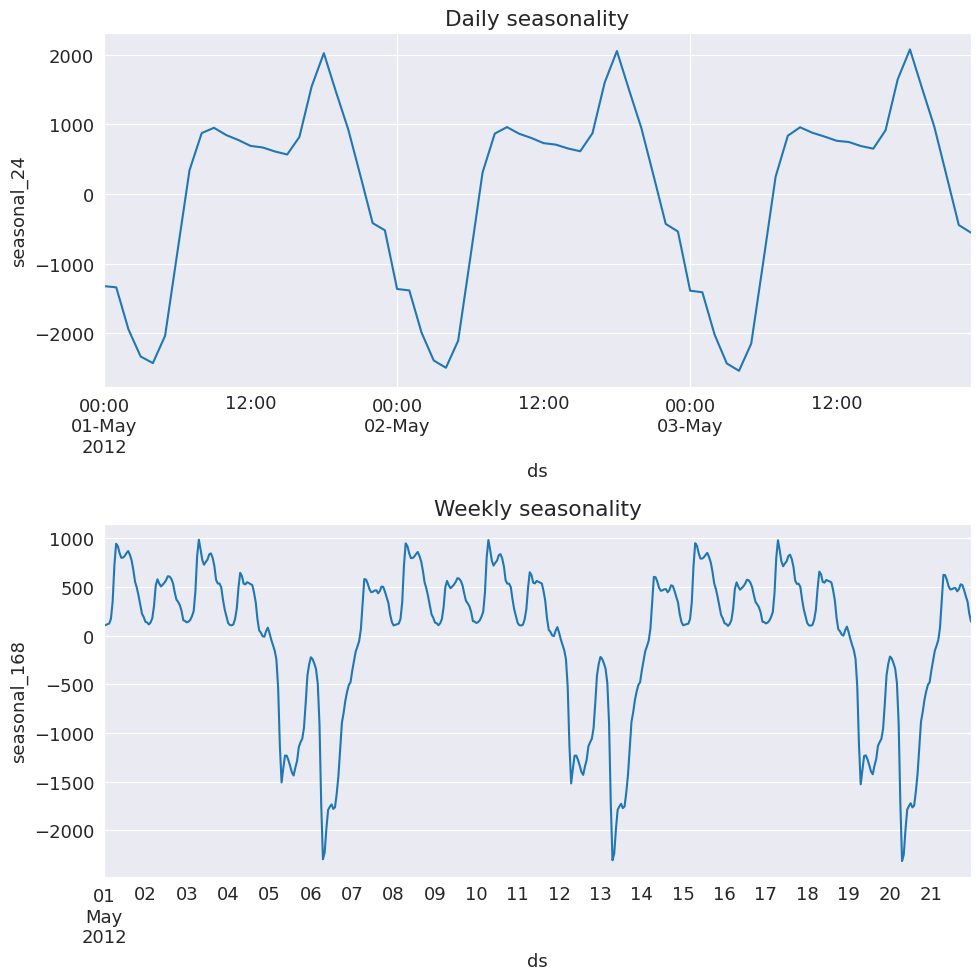
../../../_images/examples_notebooks_generated_mstl_decomposition_36_0.png

现在我们可以看到晚上还有一个额外的峰值！这可能与晚上现在需要供暖和照明有关。所以这是有道理的。我们看到周末期间需求较低的整体每周模式仍然存在。

其他成分也可以从 trend 和 resid 属性中提取

[18]:

display(res.trend.head()) # trend component
display(res.resid.head()) # residual component

ds
2012-01-01 00:00:00    10373.942662
2012-01-01 01:00:00    10363.488489
2012-01-01 02:00:00    10353.037721
2012-01-01 03:00:00    10342.590527
2012-01-01 04:00:00    10332.147100
Freq: h, Name: trend, dtype: float64

ds
2012-01-01 00:00:00   -599.619903
2012-01-01 01:00:00   -640.231767
2012-01-01 02:00:00   -644.205579
2012-01-01 03:00:00   -719.433316
2012-01-01 04:00:00   -678.424613
Freq: h, Name: resid, dtype: float64

就这样！使用 MSTL，我们可以在多重季节时间序列上执行时间序列分解！

上次更新：2024 年 10 月 3 日