马尔可夫切换自回归模型¶
本笔记本提供了一个关于在 statsmodels 中使用马尔可夫切换模型的示例,以复制 Kim 和 Nelson (1999) 中提出的许多结果。它应用了 Hamilton (1989) 滤波器和 Kim (1994) 平滑器。
这与 E-views 8 中的马尔可夫切换模型进行了测试,可以在 http://www.eviews.com/EViews8/ev8ecswitch_n.html#MarkovAR 找到,或者在 Stata 14 的马尔可夫切换模型中找到,可以在 http://www.stata.com/manuals14/tsmswitch.pdf 中找到。
[1]:
%matplotlib inline
from datetime import datetime
from io import BytesIO
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import statsmodels.api as sm
# NBER recessions
from pandas_datareader.data import DataReader
usrec = DataReader(
"USREC", "fred", start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)
)
Hamilton (1989) 切换模型的 GNP¶
这复制了 Hamilton (1989) 的开创性论文,介绍了马尔可夫切换模型。该模型是 4 阶的自回归模型,其中过程的均值在两个状态之间切换。它可以写成
每个时期,状态根据以下转移概率矩阵进行转换
其中 \(p_{ij}\) 是从状态 \(i\) 转移到状态 \(j\) 的概率。
模型类是 MarkovAutoregression,位于 statsmodels 的时间序列部分。为了创建模型,我们必须使用 k_regimes=2 指定状态数,并使用 order=4 指定自回归的阶数。默认模型还包括切换自回归系数,因此这里我们还需要指定 switching_ar=False 来避免这种情况。
创建后,模型通过最大似然估计进行 fit。在幕后,使用多个步骤的期望最大化 (EM) 算法找到良好的起始参数,并且应用拟牛顿 (BFGS) 算法来快速找到最大值。
[2]:
import requests
import shutil
def download_file(url):
local_filename = url.split('/')[-1]
with requests.get(url, stream=True) as r:
with open(local_filename, 'wb') as f:
shutil.copyfileobj(r.raw, f)
return local_filename
filename = download_file("https://www.stata-press.com/data/r14/rgnp.dta")
# Get the RGNP data to replicate Hamilton
dta = pd.read_stata(filename).iloc[1:]
dta.index = pd.DatetimeIndex(dta.date, freq="QS")
dta_hamilton = dta.rgnp
# Plot the data
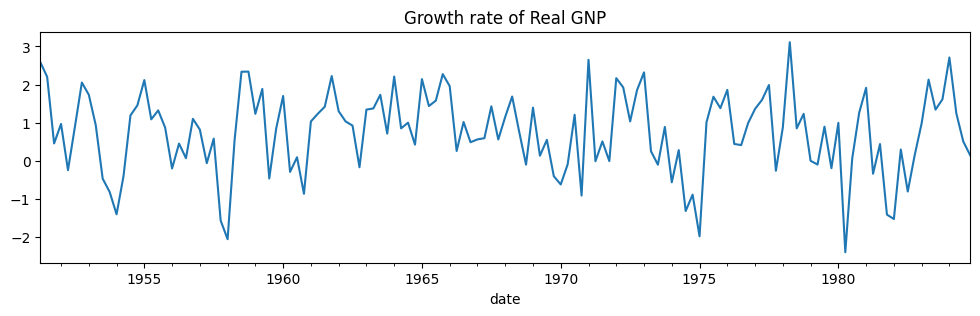
dta_hamilton.plot(title="Growth rate of Real GNP", figsize=(12, 3))
# Fit the model
mod_hamilton = sm.tsa.MarkovAutoregression(
dta_hamilton, k_regimes=2, order=4, switching_ar=False
)
res_hamilton = mod_hamilton.fit()
[3]:
res_hamilton.summary()
[3]:
| 因变量 | rgnp | 观察次数 | 131 |
|---|---|---|---|
| 模型 | MarkovAutoregression | 对数似然 | -181.263 |
| 日期 | 周四,2024 年 10 月 3 日 | AIC | 380.527 |
| 时间 | 15:44:58 | BIC | 406.404 |
| 样本 | 04-01-1951 | HQIC | 391.042 |
| - 10-01-1984 | |||
| 协方差类型 | approx |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 常数 | -0.3588 | 0.265 | -1.356 | 0.175 | -0.877 | 0.160 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 常数 | 1.1635 | 0.075 | 15.614 | 0.000 | 1.017 | 1.310 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.5914 | 0.103 | 5.761 | 0.000 | 0.390 | 0.793 |
| ar.L1 | 0.0135 | 0.120 | 0.112 | 0.911 | -0.222 | 0.249 |
| ar.L2 | -0.0575 | 0.138 | -0.418 | 0.676 | -0.327 | 0.212 |
| ar.L3 | -0.2470 | 0.107 | -2.310 | 0.021 | -0.457 | -0.037 |
| ar.L4 | -0.2129 | 0.111 | -1.926 | 0.054 | -0.430 | 0.004 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| p[0->0] | 0.7547 | 0.097 | 7.819 | 0.000 | 0.565 | 0.944 |
| p[1->0] | 0.0959 | 0.038 | 2.542 | 0.011 | 0.022 | 0.170 |
警告
[1] 使用数值 (复步) 微分计算的协方差矩阵。
我们绘制了衰退的滤波和平滑概率。滤波指的是在时间 \(t\) 基于截至时间 \(t\)(但不包括时间 \(t+1, ..., T\))的数据的概率估计。平滑指的是在时间 \(t\) 使用样本中的所有数据对概率进行的估计。
作为参考,阴影部分表示 NBER 衰退。
[4]:
fig, axes = plt.subplots(2, figsize=(7, 7))
ax = axes[0]
ax.plot(res_hamilton.filtered_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="k", alpha=0.1)
ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1])
ax.set(title="Filtered probability of recession")
ax = axes[1]
ax.plot(res_hamilton.smoothed_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="k", alpha=0.1)
ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1])
ax.set(title="Smoothed probability of recession")
fig.tight_layout()
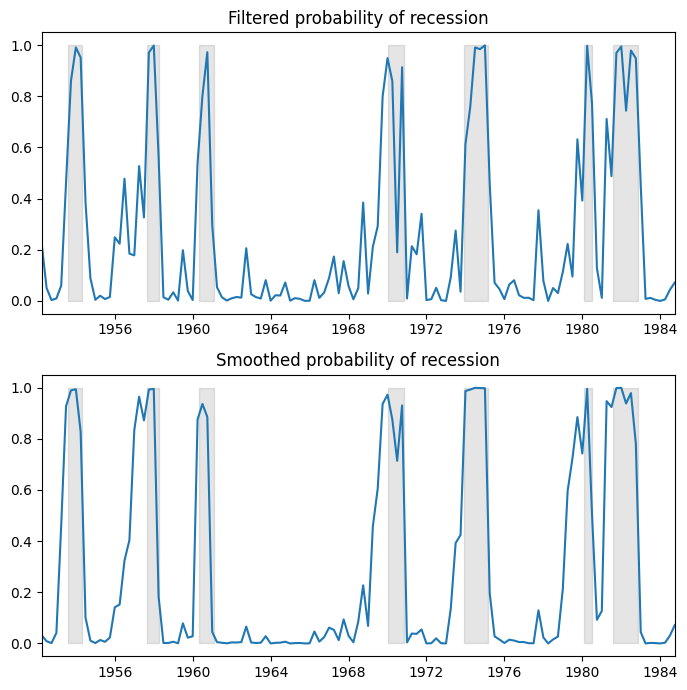
从估计的转移矩阵中,我们可以计算出衰退与扩张的预期持续时间。
[5]:
print(res_hamilton.expected_durations)
[ 4.07604744 10.42589389]
在这种情况下,预计衰退将持续大约一年(4 个季度),而扩张将持续大约两年半。
Kim, Nelson 和 Startz (1998) 三状态方差切换¶
该模型演示了具有状态异方差(方差切换)和无均值效应的估计。数据集可以在 http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn 中找到。
所讨论的模型是
由于没有自回归成分,因此可以使用 MarkovRegression 类拟合该模型。由于没有均值效应,因此我们指定 trend='n'。假设切换方差存在三个状态,因此我们指定 k_regimes=3 和 switching_variance=True(默认情况下,假定方差在各个状态之间是相同的)。
[6]:
# Get the dataset
ew_excs = requests.get("http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn").content
raw = pd.read_table(BytesIO(ew_excs), header=None, skipfooter=1, engine="python")
raw.index = pd.date_range("1926-01-01", "1995-12-01", freq="MS")
dta_kns = raw.loc[:"1986"] - raw.loc[:"1986"].mean()
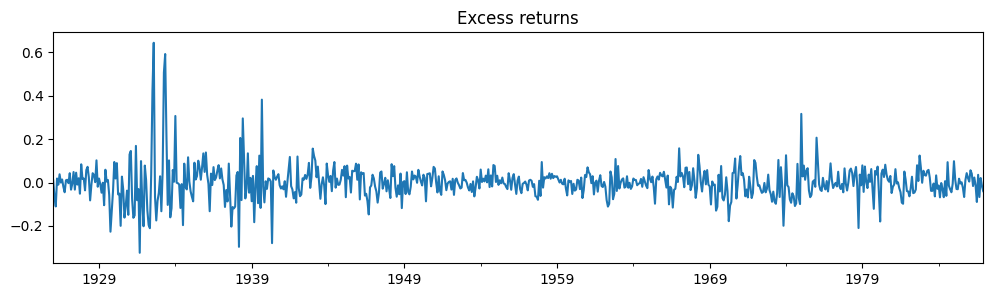
# Plot the dataset
dta_kns[0].plot(title="Excess returns", figsize=(12, 3))
# Fit the model
mod_kns = sm.tsa.MarkovRegression(
dta_kns, k_regimes=3, trend="n", switching_variance=True
)
res_kns = mod_kns.fit()
[7]:
res_kns.summary()
[7]:
| 因变量 | 0 | 观察次数 | 732 |
|---|---|---|---|
| 模型 | MarkovRegression | 对数似然 | 1001.895 |
| 日期 | 周四,2024 年 10 月 3 日 | AIC | -1985.790 |
| 时间 | 15:45:03 | BIC | -1944.428 |
| 样本 | 01-01-1926 | HQIC | -1969.834 |
| - 12-01-1986 | |||
| 协方差类型 | approx |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.0012 | 0.000 | 7.136 | 0.000 | 0.001 | 0.002 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.0040 | 0.000 | 8.489 | 0.000 | 0.003 | 0.005 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.0311 | 0.006 | 5.461 | 0.000 | 0.020 | 0.042 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| p[0->0] | 0.9747 | 0.000 | 7857.416 | 0.000 | 0.974 | 0.975 |
| p[1->0] | 0.0195 | 0.010 | 1.949 | 0.051 | -0.000 | 0.039 |
| p[2->0] | 2.354e-08 | nan | nan | nan | nan | nan |
| p[0->1] | 0.0253 | 3.97e-05 | 637.835 | 0.000 | 0.025 | 0.025 |
| p[1->1] | 0.9688 | 0.013 | 75.528 | 0.000 | 0.944 | 0.994 |
| p[2->1] | 0.0493 | 0.032 | 1.551 | 0.121 | -0.013 | 0.112 |
警告
[1] 使用数值 (复步) 微分计算的协方差矩阵。
下面我们绘制了处于每个状态的概率;只有在少数几个时期,高方差状态才有可能。
[8]:
fig, axes = plt.subplots(3, figsize=(10, 7))
ax = axes[0]
ax.plot(res_kns.smoothed_marginal_probabilities[0])
ax.set(title="Smoothed probability of a low-variance regime for stock returns")
ax = axes[1]
ax.plot(res_kns.smoothed_marginal_probabilities[1])
ax.set(title="Smoothed probability of a medium-variance regime for stock returns")
ax = axes[2]
ax.plot(res_kns.smoothed_marginal_probabilities[2])
ax.set(title="Smoothed probability of a high-variance regime for stock returns")
fig.tight_layout()
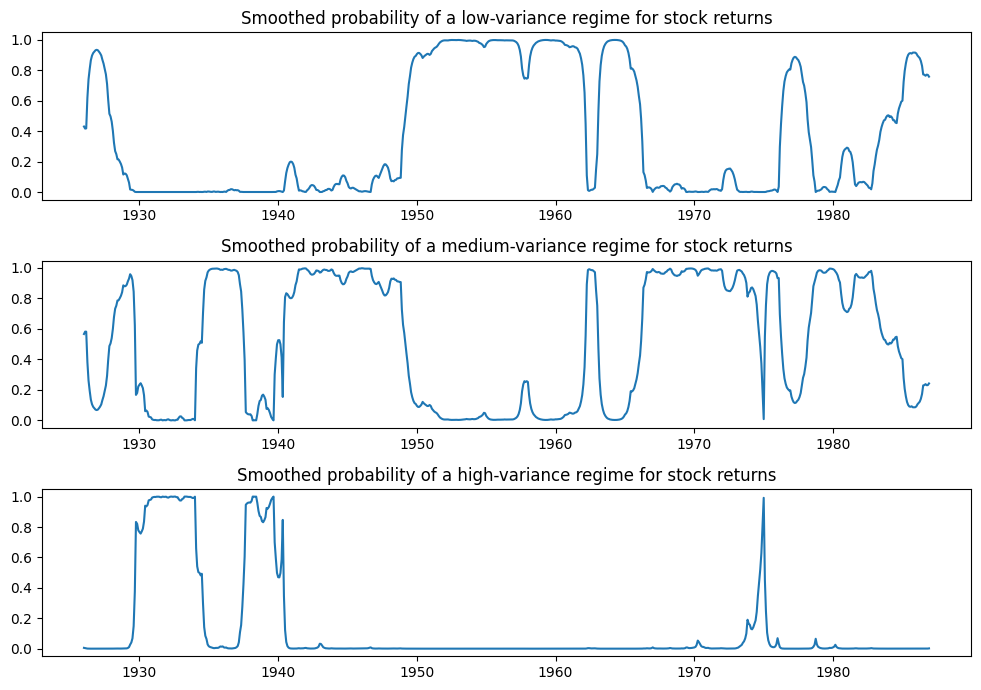
Filardo (1994) 时变转移概率¶
该模型演示了具有时变转移概率的估计。数据集可以在 http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn 中找到。
在上面的模型中,我们假设转移概率在时间上是恒定的。在这里,我们允许概率随着经济状况的变化而变化。否则,该模型与 Hamilton (1989) 的马尔可夫自回归模型相同。
每个时期,状态现在根据以下时变转移概率矩阵进行转换
其中 \(p_{ij,t}\) 是在时期 \(t\) 从状态 \(i\) 转移到状态 \(j\) 的概率,定义为
而不是将转移概率作为最大似然估计的一部分进行估计,回归系数 \(\beta_{ij}\) 是估计出来的。这些系数将转移概率与一组预先确定的或外生回归量 \(x_{t-1}\) 相关联。
[9]:
# Get the dataset
filardo = requests.get("http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn").content
dta_filardo = pd.read_table(
BytesIO(filardo), sep=" +", header=None, skipfooter=1, engine="python"
)
dta_filardo.columns = ["month", "ip", "leading"]
dta_filardo.index = pd.date_range("1948-01-01", "1991-04-01", freq="MS")
dta_filardo["dlip"] = np.log(dta_filardo["ip"]).diff() * 100
# Deflated pre-1960 observations by ratio of std. devs.
# See hmt_tvp.opt or Filardo (1994) p. 302
std_ratio = (
dta_filardo["dlip"]["1960-01-01":].std() / dta_filardo["dlip"][:"1959-12-01"].std()
)
dta_filardo.loc[:"1959-12-01", "dlip"] = dta_filardo["dlip"][:"1959-12-01"] * std_ratio
dta_filardo["dlleading"] = np.log(dta_filardo["leading"]).diff() * 100
dta_filardo["dmdlleading"] = dta_filardo["dlleading"] - dta_filardo["dlleading"].mean()
# Plot the data
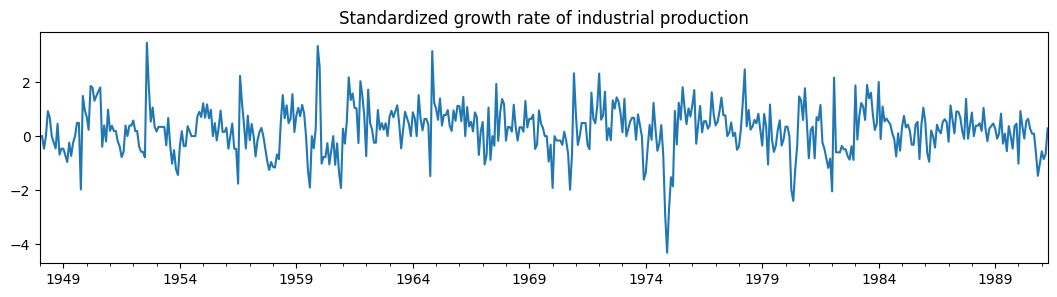
dta_filardo["dlip"].plot(
title="Standardized growth rate of industrial production", figsize=(13, 3)
)
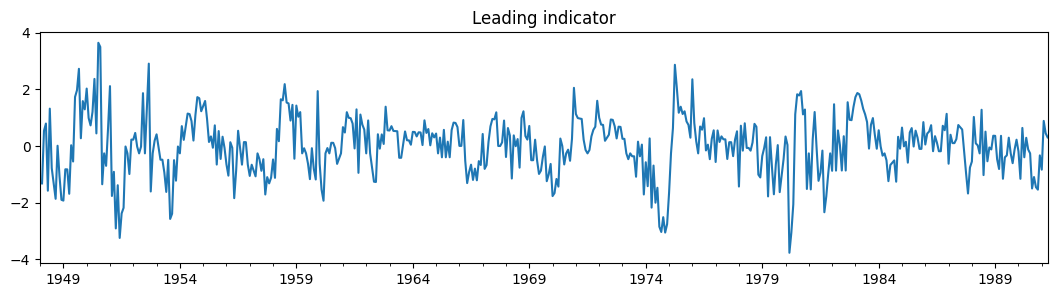
plt.figure()
dta_filardo["dmdlleading"].plot(title="Leading indicator", figsize=(13, 3))
[9]:
<Axes: title={'center': 'Leading indicator'}>
时变转移概率由 exog_tvtp 参数指定。
在这里,我们演示了模型拟合的另一个特征 - 使用随机搜索来寻找 MLE 起始参数。由于马尔可夫切换模型通常以似然函数的许多局部最大值为特征,因此执行初始优化步骤可能有助于找到最佳参数。
下面,我们指定从起始参数向量进行 20 次随机扰动,并使用最佳扰动作为实际起始参数。由于搜索的随机性,我们预先播种随机数生成器,以便能够复制结果。
[10]:
mod_filardo = sm.tsa.MarkovAutoregression(
dta_filardo.iloc[2:]["dlip"],
k_regimes=2,
order=4,
switching_ar=False,
exog_tvtp=sm.add_constant(dta_filardo.iloc[1:-1]["dmdlleading"]),
)
np.random.seed(12345)
res_filardo = mod_filardo.fit(search_reps=20)
[11]:
res_filardo.summary()
[11]:
| 因变量 | dlip | 观察次数 | 514 |
|---|---|---|---|
| 模型 | MarkovAutoregression | 对数似然 | -586.572 |
| 日期 | 周四,2024 年 10 月 3 日 | AIC | 1195.144 |
| 时间 | 15:45:14 | BIC | 1241.808 |
| 样本 | 03-01-1948 | HQIC | 1213.433 |
| - 04-01-1991 | |||
| 协方差类型 | approx |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 常数 | -0.8659 | 0.153 | -5.658 | 0.000 | -1.166 | -0.566 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 常数 | 0.5173 | 0.077 | 6.706 | 0.000 | 0.366 | 0.668 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.4844 | 0.037 | 13.172 | 0.000 | 0.412 | 0.556 |
| ar.L1 | 0.1895 | 0.050 | 3.761 | 0.000 | 0.091 | 0.288 |
| ar.L2 | 0.0793 | 0.051 | 1.552 | 0.121 | -0.021 | 0.180 |
| ar.L3 | 0.1109 | 0.052 | 2.136 | 0.033 | 0.009 | 0.213 |
| ar.L4 | 0.1223 | 0.051 | 2.418 | 0.016 | 0.023 | 0.221 |
| coef | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| p[0->0].tvtp0 | 1.6494 | 0.446 | 3.702 | 0.000 | 0.776 | 2.523 |
| p[1->0].tvtp0 | -4.3595 | 0.747 | -5.833 | 0.000 | -5.824 | -2.895 |
| p[0->0].tvtp1 | -0.9945 | 0.566 | -1.758 | 0.079 | -2.103 | 0.114 |
| p[1->0].tvtp1 | -1.7702 | 0.508 | -3.484 | 0.000 | -2.766 | -0.775 |
警告
[1] 使用数值 (复步) 微分计算的协方差矩阵。
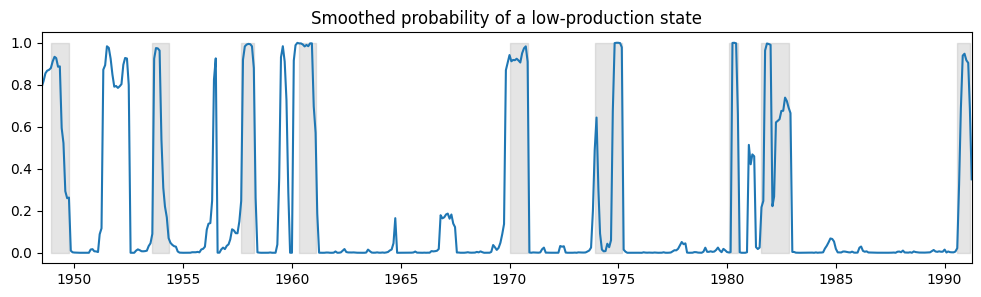
下面我们绘制了经济处于低生产状态的平滑概率,并再次包含 NBER 衰退以进行比较。
[12]:
fig, ax = plt.subplots(figsize=(12, 3))
ax.plot(res_filardo.smoothed_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="gray", alpha=0.2)
ax.set_xlim(dta_filardo.index[6], dta_filardo.index[-1])
ax.set(title="Smoothed probability of a low-production state")
[12]:
[Text(0.5, 1.0, 'Smoothed probability of a low-production state')]
使用时变转移概率,我们可以看到低生产状态的预期持续时间如何随时间变化
[13]:
res_filardo.expected_durations[0].plot(
title="Expected duration of a low-production state", figsize=(12, 3)
)
[13]:
<Axes: title={'center': 'Expected duration of a low-production state'}>
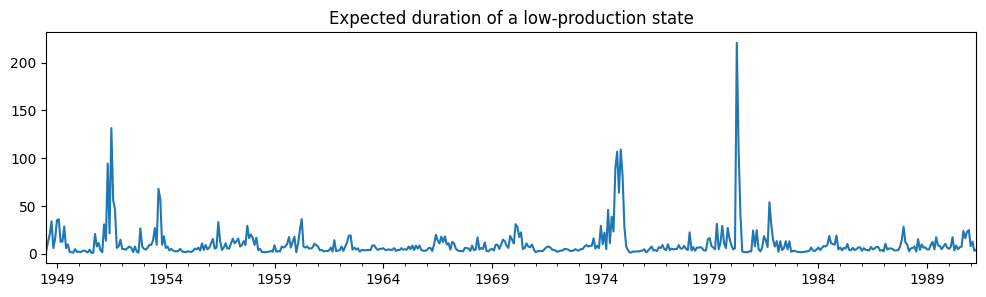
在衰退期间,低生产状态的预期持续时间远远高于扩张时期。