平稳性和去趋势 (ADF/KPSS)¶
平稳性意味着时间序列的统计特性(例如平均值、方差和协方差)不会随着时间推移而改变。许多统计模型要求序列是平稳的,以便进行有效且精确的预测。
可以使用两个统计检验来检查时间序列的平稳性 - 增广 Dickey Fuller (“ADF”) 检验和 Kwiatkowski-Phillips-Schmidt-Shin (“KPSS”) 检验。还应使用一种方法将非平稳时间序列转换为平稳序列。
第一个单元格导入标准包并将绘图设置为在内联中显示。
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
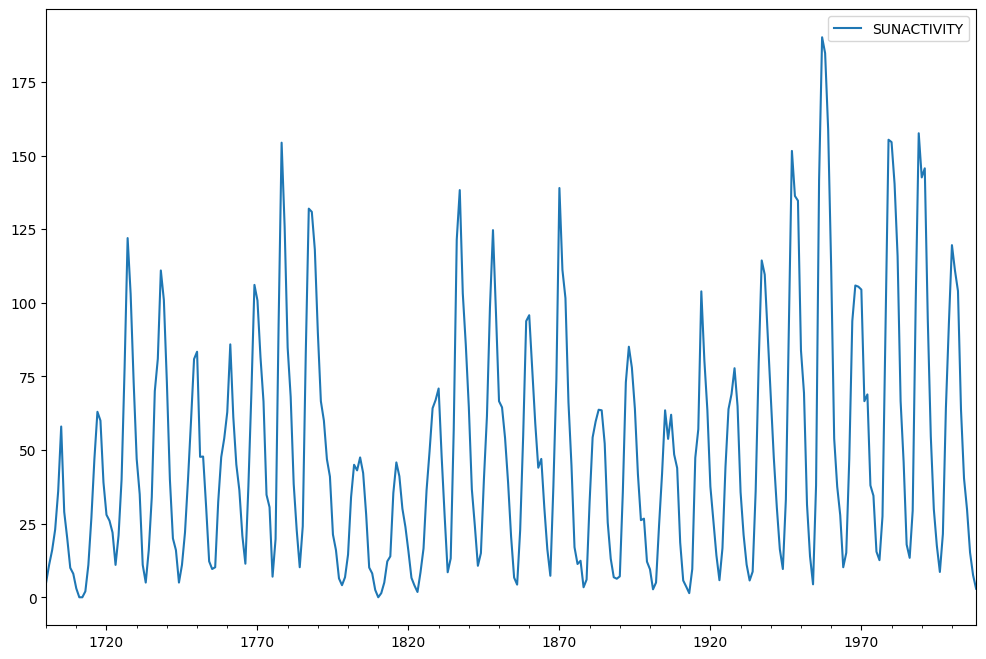
使用太阳黑子数据集。它包含来自国家地球物理数据中心的年度(1700-2008 年)太阳黑子数据。
[2]:
sunspots = sm.datasets.sunspots.load_pandas().data
对数据进行一些预处理。“YEAR” 列用于创建索引。
[3]:
sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range("1700", "2008"))
del sunspots["YEAR"]
现在绘制数据。
[4]:
sunspots.plot(figsize=(12, 8))
[4]:
<Axes: >
ADF 检验¶
ADF 检验用于确定序列中是否存在单位根,因此有助于了解序列是平稳的还是非平稳的。此检验的零假设和备择假设为
零假设:序列具有单位根。
备择假设:序列没有单位根。
如果未能拒绝零假设,此检验可能提供序列非平稳的证据。
创建一个函数来对时间序列进行 ADF 检验。
[5]:
from statsmodels.tsa.stattools import adfuller
def adf_test(timeseries):
print("Results of Dickey-Fuller Test:")
dftest = adfuller(timeseries, autolag="AIC")
dfoutput = pd.Series(
dftest[0:4],
index=[
"Test Statistic",
"p-value",
"#Lags Used",
"Number of Observations Used",
],
)
for key, value in dftest[4].items():
dfoutput["Critical Value (%s)" % key] = value
print(dfoutput)
KPSS 检验¶
KPSS 是另一种用于检查时间序列平稳性的检验。KPSS 检验的零假设和备择假设与 ADF 检验相反。
零假设:该过程是趋势平稳的。
备择假设:序列具有单位根(序列不平稳)。
创建一个函数来对时间序列进行 KPSS 检验。
[6]:
from statsmodels.tsa.stattools import kpss
def kpss_test(timeseries):
print("Results of KPSS Test:")
kpsstest = kpss(timeseries, regression="c", nlags="auto")
kpss_output = pd.Series(
kpsstest[0:3], index=["Test Statistic", "p-value", "Lags Used"]
)
for key, value in kpsstest[3].items():
kpss_output["Critical Value (%s)" % key] = value
print(kpss_output)
ADF 检验给出以下结果 - 检验统计量、p 值和 1%、5% 和 10% 置信区间处的临界值。
现在将 ADF 检验应用于数据。
[7]:
adf_test(sunspots["SUNACTIVITY"])
Results of Dickey-Fuller Test:
Test Statistic -2.837781
p-value 0.053076
#Lags Used 8.000000
Number of Observations Used 300.000000
Critical Value (1%) -3.452337
Critical Value (5%) -2.871223
Critical Value (10%) -2.571929
dtype: float64
根据 0.05 的显著性水平和 ADF 检验的 p 值,不能拒绝零假设。因此,该序列是非平稳的。
KPSS 检验给出以下结果 - 检验统计量、p 值和 1%、5% 和 10% 置信区间处的临界值。
现在将 KPSS 检验应用于数据。
[8]:
kpss_test(sunspots["SUNACTIVITY"])
Results of KPSS Test:
Test Statistic 0.669866
p-value 0.016285
Lags Used 7.000000
Critical Value (10%) 0.347000
Critical Value (5%) 0.463000
Critical Value (2.5%) 0.574000
Critical Value (1%) 0.739000
dtype: float64
根据 0.05 的显著性水平和 KPSS 检验的 p 值,有证据表明拒绝零假设而支持备择假设。因此,根据 KPSS 检验,该序列是非平稳的。
始终最好同时应用这两个检验,以确保序列确实是平稳的。应用这些平稳性检验的可能结果如下
这里,由于 ADF 检验和 KPSS 检验的结果不同,可以推断该序列是趋势平稳的,而不是严格平稳的。可以通过差分或模型拟合对序列进行去趋势。
通过差分去趋势¶
这是对时间序列进行去趋势的最简单方法之一。构建一个新的序列,其中当前时间步的值计算为原始观测值与前一时间步观测值之间的差值。
将差分应用于数据并绘制结果。
[9]:
sunspots["SUNACTIVITY_diff"] = sunspots["SUNACTIVITY"] - sunspots["SUNACTIVITY"].shift(
1
)
sunspots["SUNACTIVITY_diff"].dropna().plot(figsize=(12, 8))
[9]:
<Axes: >
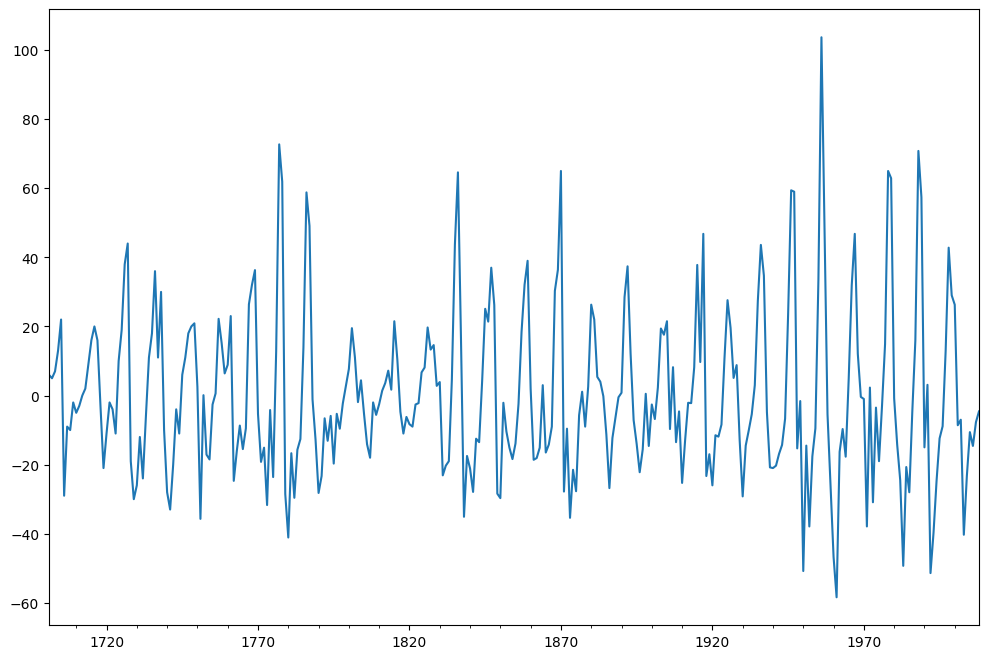
现在将 ADF 检验应用于这些去趋势值并检查平稳性。
[10]:
adf_test(sunspots["SUNACTIVITY_diff"].dropna())
Results of Dickey-Fuller Test:
Test Statistic -1.486166e+01
p-value 1.715552e-27
#Lags Used 7.000000e+00
Number of Observations Used 3.000000e+02
Critical Value (1%) -3.452337e+00
Critical Value (5%) -2.871223e+00
Critical Value (10%) -2.571929e+00
dtype: float64
根据 ADF 检验的 p 值,有证据表明拒绝零假设而支持备择假设。因此,该序列现在是严格平稳的。
现在将 KPSS 检验应用于这些去趋势值并检查平稳性。
[11]:
kpss_test(sunspots["SUNACTIVITY_diff"].dropna())
Results of KPSS Test:
Test Statistic 0.021193
p-value 0.100000
Lags Used 0.000000
Critical Value (10%) 0.347000
Critical Value (5%) 0.463000
Critical Value (2.5%) 0.574000
Critical Value (1%) 0.739000
dtype: float64
/tmp/ipykernel_4050/1512460390.py:6: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.
kpsstest = kpss(timeseries, regression="c", nlags="auto")
根据 KPSS 检验的 p 值,不能拒绝零假设。因此,该序列是平稳的。
结论¶
使用了两个用于检查时间序列平稳性的检验,即 ADF 检验和 KPSS 检验。通过差分进行去趋势。趋势平稳时间序列被转换为严格平稳时间序列。现在可以将必要的预测模型应用于平稳的时间序列数据。