ETS 模型¶
ETS 模型是一组时间序列模型,其底层状态空间模型包含一个水平成分、一个趋势成分 (T)、一个季节性成分 (S) 和一个误差项 (E)。
此笔记本展示了如何在 statsmodels 中使用它们。有关更深入的介绍,我们参考 [1] 第 8 章(免费在线资源),statsmodels 中的实现和本笔记本中使用的示例都基于此。
statsmodels 实现以下所有组合: - 加法和乘法误差模型 - 加法和乘法趋势,可能被抑制 - 加法和乘法季节性
但是,并非所有这些方法都是稳定的。有关模型稳定性的更多信息,请参考 [1] 及其引用。
[1] Hyndman,Rob J. 和 Athanasopoulos,George。预测:原理与实践,第 3 版,OTexts,2021。 https://otexts.com/fpp3/expsmooth.html
[1]:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
from statsmodels.tsa.exponential_smoothing.ets import ETSModel
[2]:
plt.rcParams["figure.figsize"] = (12, 8)
简单指数平滑¶
最简单的 ETS 模型也称为简单指数平滑。在 ETS 术语中,它对应于 (A, N, N) 模型,即一个具有加性误差、无趋势和无季节性的模型。Holt 方法的状态空间公式为
\begin{align} y_{t} &= y_{t-1} + e_t\\ l_{t} &= l_{t-1} + \alpha e_t\\ \end{align}
此状态空间公式可以转换为不同的公式,一个预测和一个平滑方程(所有 ETS 模型都可以这样做)
\begin{align} \hat{y}_{t|t-1} &= l_{t-1}\\ l_{t} &= \alpha y_{t-1} + (1 - \alpha) l_{t-1} \end{align}
这里,\(\hat{y}_{t|t-1}\) 是给定前一步信息时 \(y_t\) 的预测/预期值。在简单指数平滑模型中,预测对应于先前的水平。第二个方程(平滑方程)计算下一个水平作为先前水平和先前观测值的加权平均值。
[3]:
oildata = [
111.0091,
130.8284,
141.2871,
154.2278,
162.7409,
192.1665,
240.7997,
304.2174,
384.0046,
429.6622,
359.3169,
437.2519,
468.4008,
424.4353,
487.9794,
509.8284,
506.3473,
340.1842,
240.2589,
219.0328,
172.0747,
252.5901,
221.0711,
276.5188,
271.1480,
342.6186,
428.3558,
442.3946,
432.7851,
437.2497,
437.2092,
445.3641,
453.1950,
454.4096,
422.3789,
456.0371,
440.3866,
425.1944,
486.2052,
500.4291,
521.2759,
508.9476,
488.8889,
509.8706,
456.7229,
473.8166,
525.9509,
549.8338,
542.3405,
]
oil = pd.Series(oildata, index=pd.date_range("1965", "2013", freq="YS"))
oil.plot()
plt.ylabel("Annual oil production in Saudi Arabia (Mt)")
[3]:
Text(0, 0.5, 'Annual oil production in Saudi Arabia (Mt)')
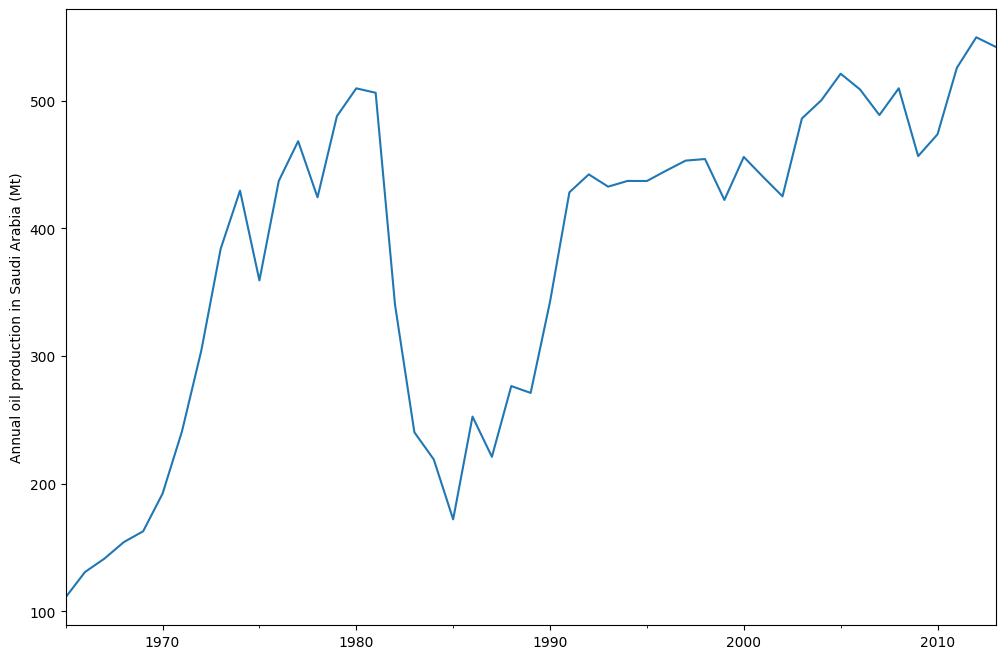
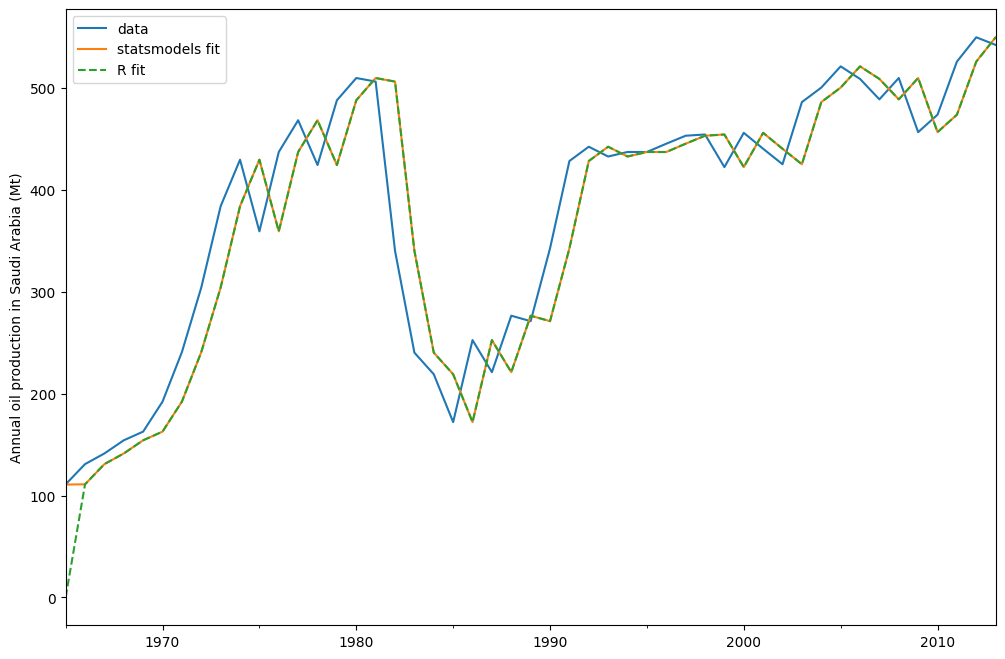
上图显示了沙特阿拉伯的年度石油产量(百万吨)。数据来自 R 包 fpp2(先前版本 [1] 的配套包)。下面您可以看到如何使用 statsmodels 的 ETS 实现将简单指数平滑模型拟合到此数据。此外,还显示了使用 R 中的 forecast 进行的拟合,以便进行比较。
[4]:
model = ETSModel(oil)
fit = model.fit(maxiter=10000)
oil.plot(label="data")
fit.fittedvalues.plot(label="statsmodels fit")
plt.ylabel("Annual oil production in Saudi Arabia (Mt)")
# obtained from R
params_R = [0.99989969, 0.11888177503085334, 0.80000197, 36.46466837, 34.72584983]
yhat = model.smooth(params_R).fittedvalues
yhat.plot(label="R fit", linestyle="--")
plt.legend()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 2 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 6.27365D+00 |proj g|= 8.99900D-01
At iterate 1 f= 5.31675D+00 |proj g|= 6.49880D-04
At iterate 2 f= 5.30939D+00 |proj g|= 5.55378D-04
At iterate 3 f= 5.29115D+00 |proj g|= 5.80869D-05
At iterate 4 f= 5.29096D+00 |proj g|= 1.95399D-06
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
2 4 13 5 0 1 1.954D-06 5.291D+00
F = 5.2909564634183583
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
[4]:
<matplotlib.legend.Legend at 0x7effba560f10>
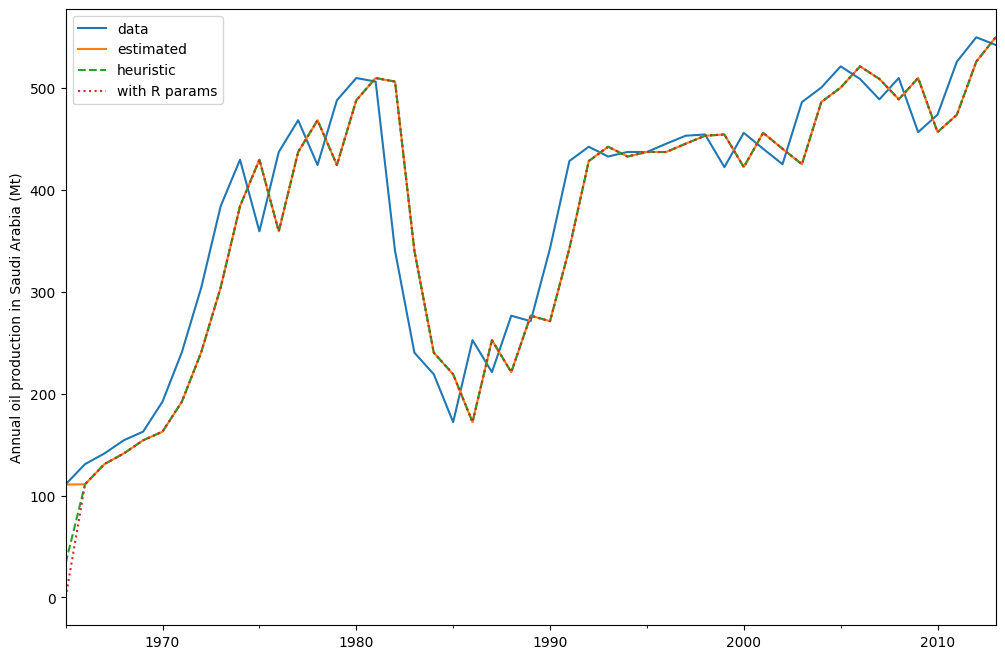
默认情况下,初始状态被认为是拟合参数,并通过最大化对数似然来估计。也可以只对初始值使用启发式方法
[5]:
model_heuristic = ETSModel(oil, initialization_method="heuristic")
fit_heuristic = model_heuristic.fit()
oil.plot(label="data")
fit.fittedvalues.plot(label="estimated")
fit_heuristic.fittedvalues.plot(label="heuristic", linestyle="--")
plt.ylabel("Annual oil production in Saudi Arabia (Mt)")
# obtained from R
params = [0.99989969, 0.11888177503085334, 0.80000197, 36.46466837, 34.72584983]
yhat = model.smooth(params).fittedvalues
yhat.plot(label="with R params", linestyle=":")
plt.legend()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 6.27365D+00 |proj g|= 8.99900D-01
At iterate 1 f= 5.31675D+00 |proj g|= 0.00000D+00
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1 1 2 1 0 1 0.000D+00 5.317D+00
F = 5.3167544390512402
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
[5]:
<matplotlib.legend.Legend at 0x7effba563940>
使用 fit.summary() 显示拟合参数和其他一些度量。在这里,我们可以看到使用拟合初始状态的模型的对数似然略低于使用初始状态的启发式方法的对数似然。
[6]:
print(fit.summary())
ETS Results
==============================================================================
Dep. Variable: y No. Observations: 49
Model: ETS(ANN) Log Likelihood -259.257
Date: Thu, 03 Oct 2024 AIC 524.514
Time: 15:51:25 BIC 530.189
Sample: 01-01-1965 HQIC 526.667
- 01-01-2013 Scale 2307.767
Covariance Type: approx
===================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
smoothing_level 0.9999 0.132 7.551 0.000 0.740 1.259
initial_level 110.7864 48.110 2.303 0.021 16.492 205.081
===================================================================================
Ljung-Box (Q): 1.87 Jarque-Bera (JB): 20.78
Prob(Q): 0.39 Prob(JB): 0.00
Heteroskedasticity (H): 0.49 Skew: -1.04
Prob(H) (two-sided): 0.16 Kurtosis: 5.42
===================================================================================
Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.
[7]:
print(fit_heuristic.summary())
ETS Results
==============================================================================
Dep. Variable: y No. Observations: 49
Model: ETS(ANN) Log Likelihood -260.521
Date: Thu, 03 Oct 2024 AIC 525.042
Time: 15:51:25 BIC 528.826
Sample: 01-01-1965 HQIC 526.477
- 01-01-2013 Scale 2429.964
Covariance Type: approx
===================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
smoothing_level 0.9999 0.132 7.559 0.000 0.741 1.259
==============================================
initialization method: heuristic
----------------------------------------------
initial_level 33.6309
===================================================================================
Ljung-Box (Q): 1.85 Jarque-Bera (JB): 18.42
Prob(Q): 0.40 Prob(JB): 0.00
Heteroskedasticity (H): 0.44 Skew: -1.02
Prob(H) (two-sided): 0.11 Kurtosis: 5.21
===================================================================================
Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.
Holt-Winters' 季节性方法¶
可以修改指数平滑方法以包含趋势和季节性成分。在加性 Holt-Winters' 方法中,季节性成分加到其余部分。此模型对应于 ETS(A, A, A) 模型,并具有以下状态空间公式
\begin{align} y_t &= l_{t-1} + b_{t-1} + s_{t-m} + e_t\\ l_{t} &= l_{t-1} + b_{t-1} + \alpha e_t\\ b_{t} &= b_{t-1} + \beta e_t\\ s_{t} &= s_{t-m} + \gamma e_t \end{align}
[8]:
austourists_data = [
30.05251300,
19.14849600,
25.31769200,
27.59143700,
32.07645600,
23.48796100,
28.47594000,
35.12375300,
36.83848500,
25.00701700,
30.72223000,
28.69375900,
36.64098600,
23.82460900,
29.31168300,
31.77030900,
35.17787700,
19.77524400,
29.60175000,
34.53884200,
41.27359900,
26.65586200,
28.27985900,
35.19115300,
42.20566386,
24.64917133,
32.66733514,
37.25735401,
45.24246027,
29.35048127,
36.34420728,
41.78208136,
49.27659843,
31.27540139,
37.85062549,
38.83704413,
51.23690034,
31.83855162,
41.32342126,
42.79900337,
55.70835836,
33.40714492,
42.31663797,
45.15712257,
59.57607996,
34.83733016,
44.84168072,
46.97124960,
60.01903094,
38.37117851,
46.97586413,
50.73379646,
61.64687319,
39.29956937,
52.67120908,
54.33231689,
66.83435838,
40.87118847,
51.82853579,
57.49190993,
65.25146985,
43.06120822,
54.76075713,
59.83447494,
73.25702747,
47.69662373,
61.09776802,
66.05576122,
]
index = pd.date_range("1999-03-01", "2015-12-01", freq="3MS")
austourists = pd.Series(austourists_data, index=index)
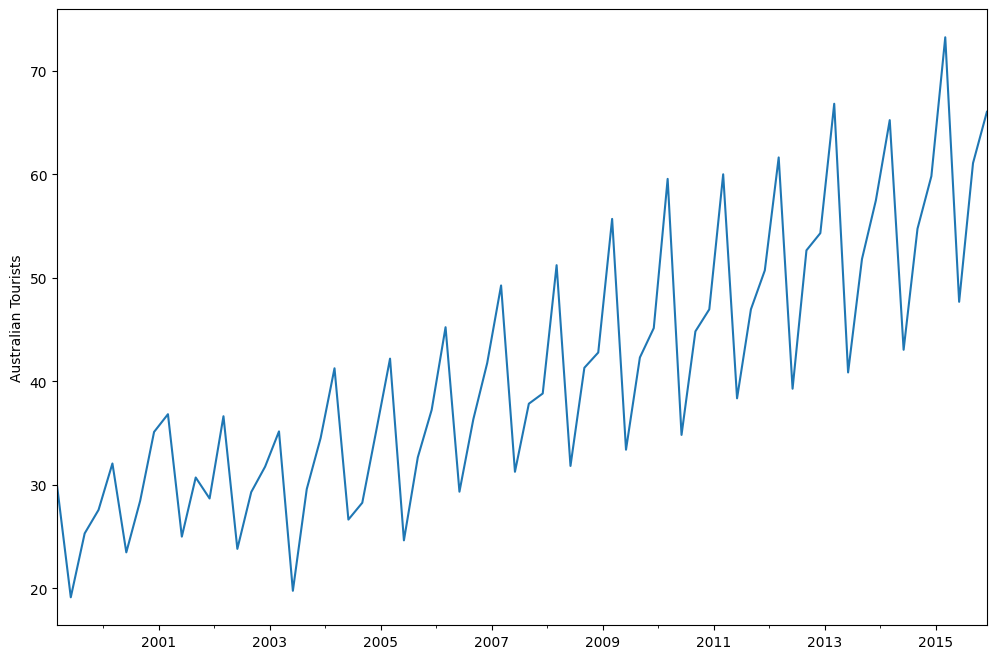
austourists.plot()
plt.ylabel("Australian Tourists")
[8]:
Text(0, 0.5, 'Australian Tourists')
[9]:
# fit in statsmodels
model = ETSModel(
austourists,
error="add",
trend="add",
seasonal="add",
damped_trend=True,
seasonal_periods=4,
)
fit = model.fit()
# fit with R params
params_R = [
0.35445427,
0.03200749,
0.39993387,
0.97999997,
24.01278357,
0.97770147,
1.76951063,
-0.50735902,
-6.61171798,
5.34956637,
]
fit_R = model.smooth(params_R)
austourists.plot(label="data")
plt.ylabel("Australian Tourists")
fit.fittedvalues.plot(label="statsmodels fit")
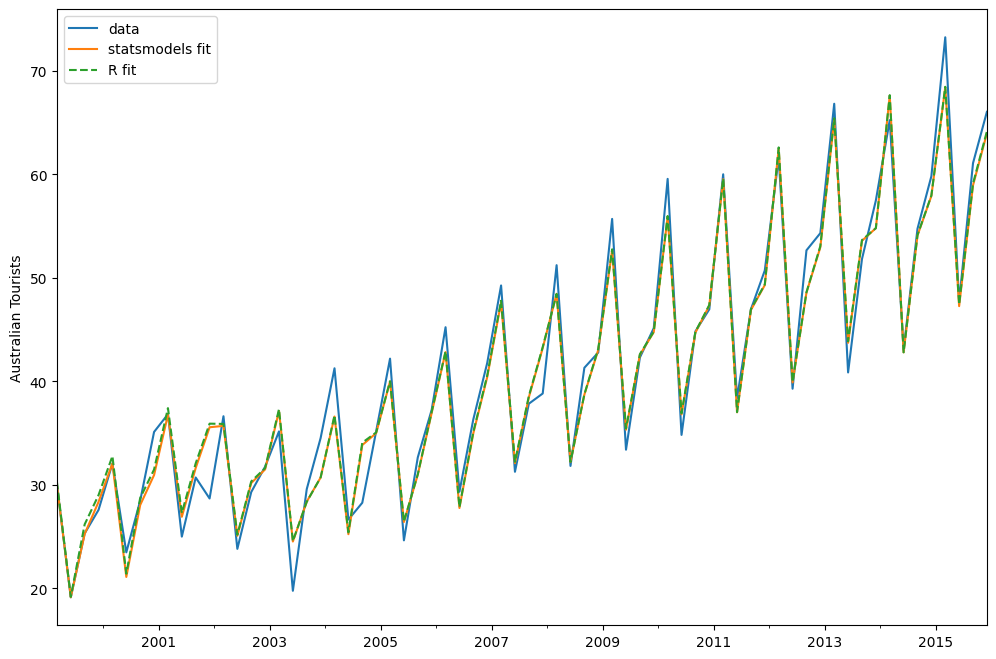
fit_R.fittedvalues.plot(label="R fit", linestyle="--")
plt.legend()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 9 M = 10
At X0 1 variables are exactly at the bounds
At iterate 0 f= 3.40132D+00 |proj g|= 9.88789D-01
At iterate 1 f= 2.58255D+00 |proj g|= 9.99244D-01
At iterate 2 f= 2.49918D+00 |proj g|= 2.90033D-01
At iterate 3 f= 2.48198D+00 |proj g|= 2.44942D-01
At iterate 4 f= 2.43118D+00 |proj g|= 7.29721D-02
At iterate 5 f= 2.42924D+00 |proj g|= 7.03572D-02
At iterate 6 f= 2.42851D+00 |proj g|= 4.66402D-02
At iterate 7 f= 2.42794D+00 |proj g|= 2.92421D-02
At iterate 8 f= 2.42784D+00 |proj g|= 2.53310D-02
At iterate 9 f= 2.42721D+00 |proj g|= 1.89539D-02
At iterate 10 f= 2.42622D+00 |proj g|= 3.18632D-02
At iterate 11 f= 2.42512D+00 |proj g|= 3.53022D-02
At iterate 12 f= 2.42383D+00 |proj g|= 3.65631D-02
At iterate 13 f= 2.42196D+00 |proj g|= 4.83553D-02
At iterate 14 f= 2.41828D+00 |proj g|= 5.99624D-02
At iterate 15 f= 2.41131D+00 |proj g|= 6.89742D-02
At iterate 16 f= 2.40200D+00 |proj g|= 7.65517D-02
At iterate 17 f= 2.39385D+00 |proj g|= 8.77242D-02
At iterate 18 f= 2.37916D+00 |proj g|= 1.52281D-01
At iterate 19 f= 2.35438D+00 |proj g|= 2.40327D-01
At iterate 20 f= 2.33828D+00 |proj g|= 2.52896D-01
At iterate 21 f= 2.33770D+00 |proj g|= 2.54660D-01
At iterate 22 f= 2.33762D+00 |proj g|= 2.49657D-01
At iterate 23 f= 2.33762D+00 |proj g|= 2.49697D-01
Positive dir derivative in projection
Using the backtracking step
At iterate 24 f= 2.32723D+00 |proj g|= 2.22951D-01
At iterate 25 f= 2.29779D+00 |proj g|= 1.15836D-01
At iterate 26 f= 2.29778D+00 |proj g|= 1.19145D-01
At iterate 27 f= 2.29778D+00 |proj g|= 1.21533D-01
At iterate 28 f= 2.29776D+00 |proj g|= 1.25497D-01
At iterate 29 f= 2.29070D+00 |proj g|= 7.52324D-02
At iterate 30 f= 2.27456D+00 |proj g|= 1.27062D-01
At iterate 31 f= 2.27409D+00 |proj g|= 8.96982D-02
At iterate 32 f= 2.27207D+00 |proj g|= 3.04527D-02
At iterate 33 f= 2.27170D+00 |proj g|= 1.70468D-02
At iterate 34 f= 2.27155D+00 |proj g|= 6.02962D-03
At iterate 35 f= 2.27150D+00 |proj g|= 4.19433D-03
At iterate 36 f= 2.27146D+00 |proj g|= 4.21130D-03
At iterate 37 f= 2.27115D+00 |proj g|= 1.59982D-02
At iterate 38 f= 2.27050D+00 |proj g|= 3.20307D-02
At iterate 39 f= 2.26874D+00 |proj g|= 5.83353D-02
At iterate 40 f= 2.26515D+00 |proj g|= 8.55094D-02
At iterate 41 f= 2.25988D+00 |proj g|= 9.47493D-02
At iterate 42 f= 2.25758D+00 |proj g|= 9.47586D-02
At iterate 43 f= 2.25540D+00 |proj g|= 3.96133D-02
At iterate 44 f= 2.25475D+00 |proj g|= 1.33489D-02
At iterate 45 f= 2.25465D+00 |proj g|= 8.38312D-03
At iterate 46 f= 2.25460D+00 |proj g|= 8.52429D-03
At iterate 47 f= 2.25451D+00 |proj g|= 1.19320D-02
At iterate 48 f= 2.25426D+00 |proj g|= 1.47960D-02
At iterate 49 f= 2.25359D+00 |proj g|= 2.79243D-02
At iterate 50 f= 2.25224D+00 |proj g|= 4.37239D-02
At iterate 51 f= 2.24962D+00 |proj g|= 5.66733D-02
At iterate 52 f= 2.24765D+00 |proj g|= 3.81767D-02
At iterate 53 f= 2.24588D+00 |proj g|= 3.82196D-02
At iterate 54 f= 2.24494D+00 |proj g|= 1.60805D-02
At iterate 55 f= 2.24481D+00 |proj g|= 1.56917D-02
At iterate 56 f= 2.24474D+00 |proj g|= 3.92202D-03
At iterate 57 f= 2.24470D+00 |proj g|= 4.88161D-03
At iterate 58 f= 2.24469D+00 |proj g|= 3.55689D-03
At iterate 59 f= 2.24469D+00 |proj g|= 1.18479D-03
At iterate 60 f= 2.24469D+00 |proj g|= 2.07274D-03
At iterate 61 f= 2.24468D+00 |proj g|= 4.24549D-03
At iterate 62 f= 2.24467D+00 |proj g|= 8.14029D-03
At iterate 63 f= 2.24464D+00 |proj g|= 1.21072D-02
At iterate 64 f= 2.24459D+00 |proj g|= 1.40037D-02
At iterate 65 f= 2.24454D+00 |proj g|= 9.93254D-03
At iterate 66 f= 2.24452D+00 |proj g|= 3.11324D-03
At iterate 67 f= 2.24452D+00 |proj g|= 6.95177D-04
At iterate 68 f= 2.24452D+00 |proj g|= 1.09637D-03
At iterate 69 f= 2.24452D+00 |proj g|= 1.09606D-03
At iterate 70 f= 2.24451D+00 |proj g|= 6.25722D-04
At iterate 71 f= 2.24451D+00 |proj g|= 3.55094D-04
At iterate 72 f= 2.24451D+00 |proj g|= 8.03047D-04
At iterate 73 f= 2.24451D+00 |proj g|= 2.00062D-04
At iterate 74 f= 2.24451D+00 |proj g|= 1.43974D-04
At iterate 75 f= 2.24451D+00 |proj g|= 3.35287D-05
At iterate 76 f= 2.24451D+00 |proj g|= 6.60361D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
9 76 95 84 0 1 6.604D-05 2.245D+00
F = 2.2445127181049198
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
[9]:
<matplotlib.legend.Legend at 0x7effba13d180>
[10]:
print(fit.summary())
ETS Results
==============================================================================
Dep. Variable: y No. Observations: 68
Model: ETS(AAdA) Log Likelihood -152.627
Date: Thu, 03 Oct 2024 AIC 327.254
Time: 15:51:27 BIC 351.668
Sample: 03-01-1999 HQIC 336.928
- 12-01-2015 Scale 5.213
Covariance Type: approx
======================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------
smoothing_level 0.3399 0.111 3.070 0.002 0.123 0.557
smoothing_trend 0.0259 0.008 3.154 0.002 0.010 0.042
smoothing_seasonal 0.4010 0.080 5.041 0.000 0.245 0.557
damping_trend 0.9800 nan nan nan nan nan
initial_level 29.4409 4.74e+04 0.001 1.000 -9.28e+04 9.29e+04
initial_trend 0.6147 0.392 1.567 0.117 -0.154 1.383
initial_seasonal.0 -3.4320 4.74e+04 -7.24e-05 1.000 -9.29e+04 9.28e+04
initial_seasonal.1 -5.9481 4.74e+04 -0.000 1.000 -9.29e+04 9.28e+04
initial_seasonal.2 -11.4855 4.74e+04 -0.000 1.000 -9.29e+04 9.28e+04
initial_seasonal.3 0 4.74e+04 0 1.000 -9.28e+04 9.28e+04
===================================================================================
Ljung-Box (Q): 5.76 Jarque-Bera (JB): 7.70
Prob(Q): 0.67 Prob(JB): 0.02
Heteroskedasticity (H): 0.46 Skew: -0.63
Prob(H) (two-sided): 0.07 Kurtosis: 4.05
===================================================================================
Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.
预测¶
ETS 模型也可用于预测。有多种不同的方法可用: - forecast:进行样本外预测 - predict:样本内和样本外预测 - simulate:运行状态空间模型的模拟 - get_prediction:样本内和样本外预测,以及预测区间
我们可以在之前拟合的模型上使用它们来预测 2014 年到 2020 年。
[11]:
pred = fit.get_prediction(start="2014", end="2020")
[12]:
df = pred.summary_frame(alpha=0.05)
df
[12]:
| 均值 | pi_lower | pi_upper | |
|---|---|---|---|
| 2014-03-01 | 67.610926 | 63.135953 | 72.085899 |
| 2014-06-01 | 42.814534 | 38.339561 | 47.289507 |
| 2014-09-01 | 54.106399 | 49.631426 | 58.581372 |
| 2014-12-01 | 57.928232 | 53.453259 | 62.403204 |
| 2015-03-01 | 68.422037 | 63.947064 | 72.897010 |
| 2015-06-01 | 47.278132 | 42.803159 | 51.753105 |
| 2015-09-01 | 58.954911 | 54.479938 | 63.429884 |
| 2015-12-01 | 63.982281 | 59.507308 | 68.457254 |
| 2016-03-01 | 75.905266 | 71.430293 | 80.380239 |
| 2016-06-01 | 51.417926 | 46.653727 | 56.182125 |
| 2016-09-01 | 63.703065 | 58.628997 | 68.777133 |
| 2016-12-01 | 67.977755 | 62.575199 | 73.380311 |
| 2017-03-01 | 78.315246 | 71.735000 | 84.895491 |
| 2017-06-01 | 53.779706 | 46.882508 | 60.676903 |
| 2017-09-01 | 66.017609 | 58.787255 | 73.247964 |
| 2017-12-01 | 70.246008 | 62.667652 | 77.824364 |
| 2018-03-01 | 80.538134 | 71.891483 | 89.184785 |
| 2018-06-01 | 55.958136 | 46.966880 | 64.949392 |
| 2018-09-01 | 68.152471 | 58.803847 | 77.501095 |
| 2018-12-01 | 72.338173 | 62.620421 | 82.055925 |
| 2019-03-01 | 82.588455 | 71.863153 | 93.313757 |
| 2019-06-01 | 57.967451 | 46.874297 | 69.060605 |
| 2019-09-01 | 70.121600 | 58.650477 | 81.592722 |
| 2019-12-01 | 74.267919 | 62.409479 | 86.126358 |
| 2020-03-01 | 84.479606 | 71.654614 | 97.304598 |
在这种情况下,预测区间是使用解析公式计算的。这并非适用于所有模型。对于这些其他模型,预测区间是通过执行多次模拟(默认情况下为 1000 次)并使用模拟结果的百分位数来计算的。这是由 get_prediction 方法在内部完成的。
我们也可以手动运行模拟,例如绘制模拟结果。由于数据范围到 2015 年底,因此我们必须从 2016 年第一季度模拟到 2020 年第一季度,这意味着 17 个步骤。
[13]:
simulated = fit.simulate(anchor="end", nsimulations=17, repetitions=100)
[14]:
for i in range(simulated.shape[1]):
simulated.iloc[:, i].plot(label="_", color="gray", alpha=0.1)
df["mean"].plot(label="mean prediction")
df["pi_lower"].plot(linestyle="--", color="tab:blue", label="95% interval")
df["pi_upper"].plot(linestyle="--", color="tab:blue", label="_")
pred.endog.plot(label="data")
plt.legend()
[14]:
<matplotlib.legend.Legend at 0x7effb7fdea40>
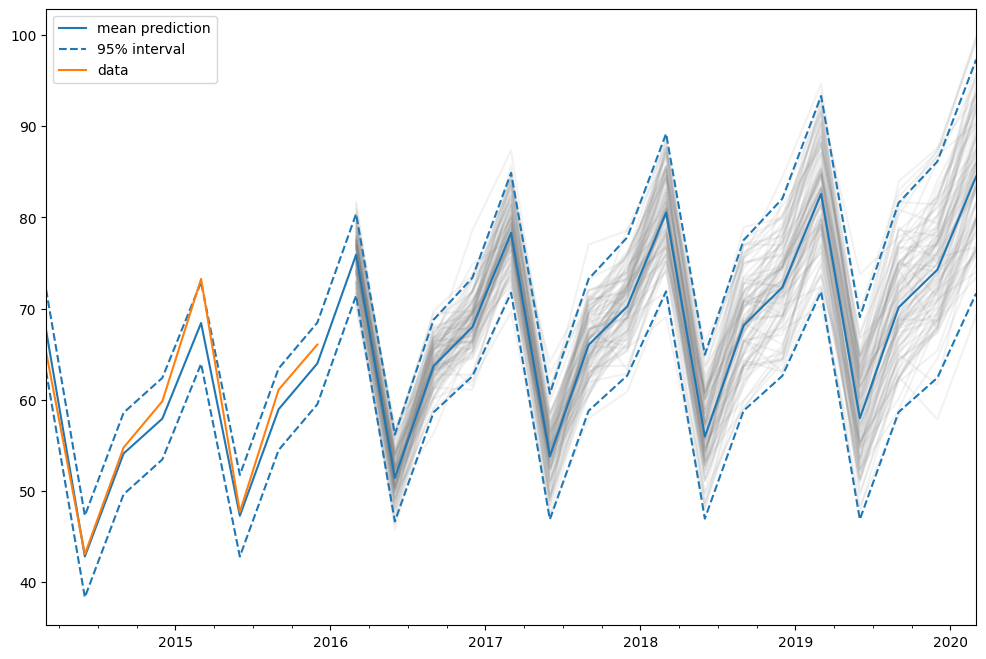
在这种情况下,我们选择“end”作为模拟锚,这意味着第一个模拟值将是第一个样本外值。也可以选择样本内的其他锚点。