失业率趋势和周期¶
在这里,我们考虑三种方法来分离经济数据中的趋势和周期。假设我们有一个时间序列 \(y_t\),基本思想是将它分解成这两个组成部分
\[y_t = \mu_t + \eta_t\]
其中 \(\mu_t\) 代表趋势或水平,而 \(\eta_t\) 代表周期性分量。在这种情况下,我们考虑一个随机趋势,因此 \(\mu_t\) 是一个随机变量,而不是时间的确定性函数。两种方法属于“未观测分量”模型,第三种是流行的霍德里克-普雷斯科特 (HP) 滤波器。与例如 Harvey 和 Jaeger (1993) 一致,我们发现这些模型都产生了相似的分解。
此笔记本演示了将这些模型应用于美国失业率以分离趋势和周期。
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
[3]:
from pandas_datareader.data import DataReader
endog = DataReader('UNRATE', 'fred', start='1954-01-01')
endog.index.freq = endog.index.inferred_freq
霍德里克-普雷斯科特 (HP) 滤波器¶
第一种方法是霍德里克-普雷斯科特 滤波器,它可以以非常直接的方法应用于数据序列。这里我们指定参数 \(\lambda=129600\),因为失业率是每月观测的。
[4]:
hp_cycle, hp_trend = sm.tsa.filters.hpfilter(endog, lamb=129600)
未观测分量和 ARIMA 模型 (UC-ARIMA)¶
下一个方法是未观测分量模型,其中趋势被建模为随机游走,周期被建模为 ARIMA 模型 - 特别是,这里我们使用 AR(4) 模型。时间序列的过程可以写成
\[\begin{split}\begin{align} y_t & = \mu_t + \eta_t \\ \mu_{t+1} & = \mu_t + \epsilon_{t+1} \\ \phi(L) \eta_t & = \nu_t \end{align}\end{split}\]
其中 \(\phi(L)\) 是 AR(4) 滞后多项式,\(\epsilon_t\) 和 \(\nu_t\) 是白噪声。
[5]:
mod_ucarima = sm.tsa.UnobservedComponents(endog, 'rwalk', autoregressive=4)
# Here the powell method is used, since it achieves a
# higher loglikelihood than the default L-BFGS method
res_ucarima = mod_ucarima.fit(method='powell', disp=False)
print(res_ucarima.summary())
Unobserved Components Results
==============================================================================
Dep. Variable: UNRATE No. Observations: 848
Model: random walk Log Likelihood -463.716
+ AR(4) AIC 939.431
Date: Thu, 03 Oct 2024 BIC 967.881
Time: 15:46:35 HQIC 950.331
Sample: 01-01-1954
- 08-01-2024
Covariance Type: opg
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
sigma2.level 5.487e-08 0.011 4.92e-06 1.000 -0.022 0.022
sigma2.ar 0.1746 0.015 11.697 0.000 0.145 0.204
ar.L1 1.0256 0.019 54.095 0.000 0.988 1.063
ar.L2 -0.1059 0.016 -6.600 0.000 -0.137 -0.074
ar.L3 0.0756 0.023 3.271 0.001 0.030 0.121
ar.L4 -0.0267 0.019 -1.421 0.155 -0.064 0.010
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 6657871.78
Prob(Q): 0.97 Prob(JB): 0.00
Heteroskedasticity (H): 9.13 Skew: 17.46
Prob(H) (two-sided): 0.00 Kurtosis: 435.94
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
具有随机周期的未观测分量 (UC)¶
最后一种方法也是一个未观测分量模型,但周期被明确建模。
\[\begin{split}\begin{align} y_t & = \mu_t + \eta_t \\ \mu_{t+1} & = \mu_t + \epsilon_{t+1} \\ \eta_{t+1} & = \eta_t \cos \lambda_\eta + \eta_t^* \sin \lambda_\eta + \tilde \omega_t \qquad & \tilde \omega_t \sim N(0, \sigma_{\tilde \omega}^2) \\ \eta_{t+1}^* & = -\eta_t \sin \lambda_\eta + \eta_t^* \cos \lambda_\eta + \tilde \omega_t^* & \tilde \omega_t^* \sim N(0, \sigma_{\tilde \omega}^2) \end{align}\end{split}\]
[6]:
mod_uc = sm.tsa.UnobservedComponents(
endog, 'rwalk',
cycle=True, stochastic_cycle=True, damped_cycle=True,
)
# Here the powell method gets close to the optimum
res_uc = mod_uc.fit(method='powell', disp=False)
# but to get to the highest loglikelihood we do a
# second round using the L-BFGS method.
res_uc = mod_uc.fit(res_uc.params, disp=False)
print(res_uc.summary())
Unobserved Components Results
=====================================================================================
Dep. Variable: UNRATE No. Observations: 848
Model: random walk Log Likelihood -472.478
+ damped stochastic cycle AIC 952.956
Date: Thu, 03 Oct 2024 BIC 971.913
Time: 15:46:37 HQIC 960.219
Sample: 01-01-1954
- 08-01-2024
Covariance Type: opg
===================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
sigma2.level 0.0183 0.033 0.552 0.581 -0.047 0.083
sigma2.cycle 0.1539 0.032 4.740 0.000 0.090 0.217
frequency.cycle 0.0437 0.029 1.495 0.135 -0.014 0.101
damping.cycle 0.9562 0.019 51.074 0.000 0.919 0.993
===================================================================================
Ljung-Box (L1) (Q): 1.53 Jarque-Bera (JB): 6560083.72
Prob(Q): 0.22 Prob(JB): 0.00
Heteroskedasticity (H): 9.47 Skew: 17.32
Prob(H) (two-sided): 0.00 Kurtosis: 433.26
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
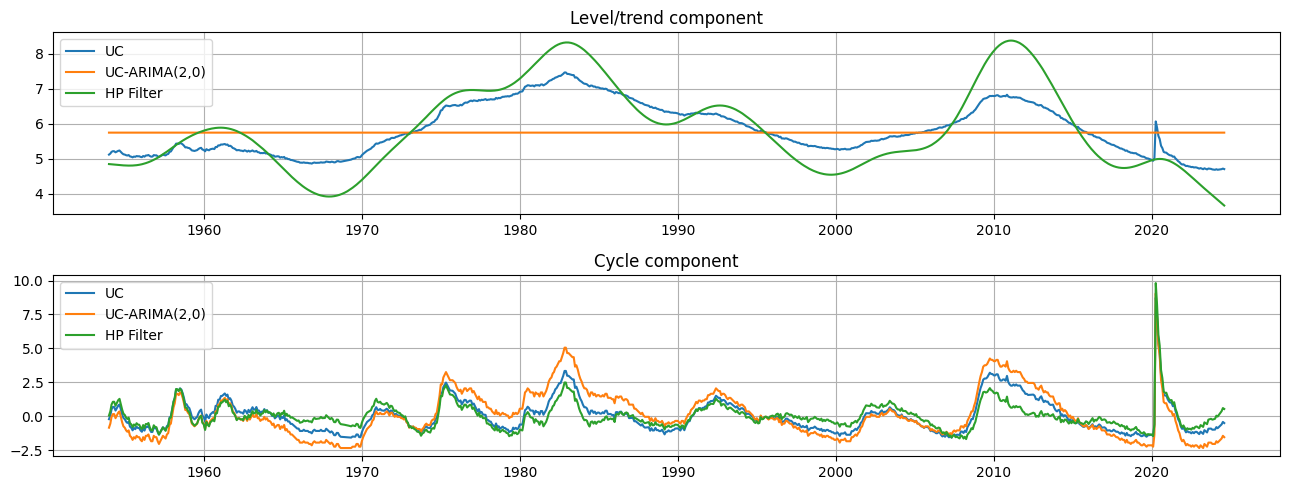
图形比较¶
这些模型的输出是趋势分量 \(\mu_t\) 的估计值和周期性分量 \(\eta_t\) 的估计值。从定性上讲,趋势和周期的估计值非常相似,尽管 HP 滤波器中的趋势分量比未观测分量模型中的趋势分量变化更大。这意味着,失业率变化中的相对模式归因于潜在趋势的变化,而不是暂时的周期性变化。
[7]:
fig, axes = plt.subplots(2, figsize=(13,5));
axes[0].set(title='Level/trend component')
axes[0].plot(endog.index, res_uc.level.smoothed, label='UC')
axes[0].plot(endog.index, res_ucarima.level.smoothed, label='UC-ARIMA(2,0)')
axes[0].plot(hp_trend, label='HP Filter')
axes[0].legend(loc='upper left')
axes[0].grid()
axes[1].set(title='Cycle component')
axes[1].plot(endog.index, res_uc.cycle.smoothed, label='UC')
axes[1].plot(endog.index, res_ucarima.autoregressive.smoothed, label='UC-ARIMA(2,0)')
axes[1].plot(hp_cycle, label='HP Filter')
axes[1].legend(loc='upper left')
axes[1].grid()
fig.tight_layout();
最后更新:2024 年 10 月 3 日