状态空间模型中的参数估计或指定¶
在本笔记本中，我们将展示如何在 statsmodels 的状态空间模型中固定某些参数的特定值，同时估计其他参数。
通常，状态空间模型允许用户
通过最大似然估计所有参数
固定一些参数并估计其余参数
固定所有参数（以便不估计任何参数）
[1]:
%matplotlib inline
from importlib import reload
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from pandas_datareader.data import DataReader
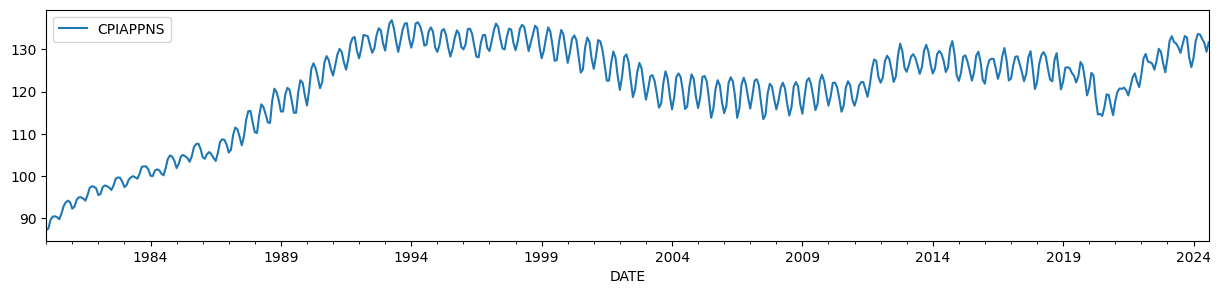
为了说明，我们将使用服装的消费者价格指数，该指数具有随时间变化的水平和强烈的季节性成分。
[2]:
endog = DataReader('CPIAPPNS', 'fred', start='1980').asfreq('MS')
endog.plot(figsize=(15, 3));
众所周知（例如，Harvey 和 Jaeger [1993]），HP 滤波器输出可以通过在参数上施加某些限制的非观测成分模型生成。
非观测成分模型为
\[\begin{split}\begin{aligned} y_t & = \mu_t + \varepsilon_t & \varepsilon_t \sim N(0, \sigma_\varepsilon^2) \\ \mu_t &= \mu_{t-1} + \beta_{t-1} + \eta_t & \eta_t \sim N(0, \sigma_\eta^2) \\ \beta_t &= \beta_{t-1} + \zeta_t & \zeta_t \sim N(0, \sigma_\zeta^2) \\ \end{aligned}\end{split}\]
为了使趋势与 HP 滤波器的输出相匹配，参数必须设置为如下所示
\[\begin{split}\begin{aligned} \frac{\sigma_\varepsilon^2}{\sigma_\zeta^2} & = \lambda \\ \sigma_\eta^2 & = 0 \end{aligned}\end{split}\]
其中 \(\lambda\) 是相关 HP 滤波器的参数。对于我们在此使用的月度数据，通常建议 \(\lambda = 129600\)。
[3]:
# Run the HP filter with lambda = 129600
hp_cycle, hp_trend = sm.tsa.filters.hpfilter(endog, lamb=129600)
# The unobserved components model above is the local linear trend, or "lltrend", specification
mod = sm.tsa.UnobservedComponents(endog, 'lltrend')
print(mod.param_names)
['sigma2.irregular', 'sigma2.level', 'sigma2.trend']
非观测成分模型 (UCM) 的参数写为
\(\sigma_\varepsilon^2 = \text{sigma2.irregular}\)
\(\sigma_\eta^2 = \text{sigma2.level}\)
\(\sigma_\zeta^2 = \text{sigma2.trend}\)
为了满足上述限制，我们将设置 \((\sigma_\varepsilon^2, \sigma_\eta^2, \sigma_\zeta^2) = (1, 0, 1 / 129600)\)。
由于我们在此固定所有参数，因此我们根本不需要使用 fit 方法，因为该方法用于执行最大似然估计。相反，我们可以直接使用 smooth 方法在选定的参数上运行卡尔曼滤波器和平滑器。
[4]:
res = mod.smooth([1., 0, 1. / 129600])
print(res.summary())
Unobserved Components Results
==============================================================================
Dep. Variable: CPIAPPNS No. Observations: 536
Model: local linear trend Log Likelihood -2997.309
Date: Thu, 03 Oct 2024 AIC 6000.619
Time: 15:45:23 BIC 6013.460
Sample: 01-01-1980 HQIC 6005.643
- 08-01-2024
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 1.0000 0.009 115.621 0.000 0.983 1.017
sigma2.level 0 0.000 0 1.000 -0.000 0.000
sigma2.trend 7.716e-06 1.98e-07 38.962 0.000 7.33e-06 8.1e-06
===================================================================================
Ljung-Box (L1) (Q): 254.28 Jarque-Bera (JB): 1.58
Prob(Q): 0.00 Prob(JB): 0.45
Heteroskedasticity (H): 2.21 Skew: 0.04
Prob(H) (two-sided): 0.00 Kurtosis: 2.75
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
与 HP 滤波器趋势估计相对应的估计由 level 的平滑估计给出（在上述符号中为 \(\mu_t\)）
[5]:
ucm_trend = pd.Series(res.level.smoothed, index=endog.index)
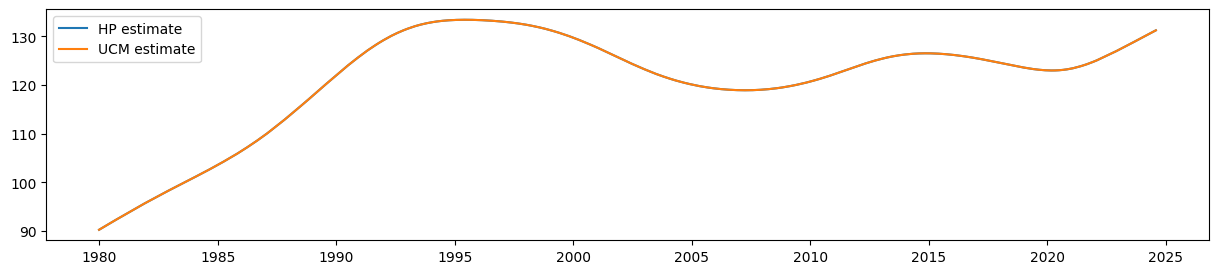
很容易看出，UCM 平滑水平的估计等于 HP 滤波器的输出
[6]:
fig, ax = plt.subplots(figsize=(15, 3))
ax.plot(hp_trend, label='HP estimate')
ax.plot(ucm_trend, label='UCM estimate')
ax.legend();
添加季节性成分¶
然而，非观测成分模型比 HP 滤波器更灵活。例如，上面显示的数据显然具有季节性，但具有随时间变化的季节性效应（季节性在开始时比在结束时弱得多）。非观测成分框架的优势之一是我们可以添加随机季节性成分。在这种情况下，我们将通过最大似然估计季节性成分的方差，同时仍然包含上述参数的限制，以便趋势对应于 HP 滤波器概念。
添加随机季节性成分会增加一个新的参数，sigma2.seasonal。
[7]:
# Construct a local linear trend model with a stochastic seasonal component of period 1 year
mod = sm.tsa.UnobservedComponents(endog, 'lltrend', seasonal=12, stochastic_seasonal=True)
print(mod.param_names)
['sigma2.irregular', 'sigma2.level', 'sigma2.trend', 'sigma2.seasonal']
在这种情况下，我们将继续像上面描述的那样限制前三个参数，但我们希望通过最大似然估计 sigma2.seasonal 的值。因此，我们将使用 fit 方法以及 fix_params 上下文管理器。
fix_params 方法接受参数名称和关联值的字典。在生成的上下文中，这些参数将在所有情况下使用。对于 fit 方法，只有未固定的参数将被估计。
[8]:
# Here we restrict the first three parameters to specific values
with mod.fix_params({'sigma2.irregular': 1, 'sigma2.level': 0, 'sigma2.trend': 1. / 129600}):
# Now we fit any remaining parameters, which in this case
# is just `sigma2.seasonal`
res_restricted = mod.fit()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 3.87642D+00 |proj g|= 2.27476D-01
At iterate 5 f= 3.25868D+00 |proj g|= 2.20983D-06
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1 5 12 1 0 0 2.210D-06 3.259D+00
F = 3.2586810226319427
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
或者，我们可以简单地使用 fit_constrained 方法，该方法也接受约束字典
[9]:
res_restricted = mod.fit_constrained({'sigma2.irregular': 1, 'sigma2.level': 0, 'sigma2.trend': 1. / 129600})
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 3.87642D+00 |proj g|= 2.27476D-01
At iterate 5 f= 3.25868D+00 |proj g|= 2.20983D-06
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1 5 12 1 0 0 2.210D-06 3.259D+00
F = 3.2586810226319427
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
摘要输出包括所有参数，但表明前三个是固定的（因此未被估计）。
[10]:
print(res_restricted.summary())
Unobserved Components Results
=====================================================================================
Dep. Variable: CPIAPPNS No. Observations: 536
Model: local linear trend Log Likelihood -1746.653
+ stochastic seasonal(12) AIC 3495.306
Date: Thu, 03 Oct 2024 BIC 3499.566
Time: 15:45:24 HQIC 3496.974
Sample: 01-01-1980
- 08-01-2024
Covariance Type: opg
============================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------------
sigma2.irregular (fixed) 1.0000 nan nan nan nan nan
sigma2.level (fixed) 0 nan nan nan nan nan
sigma2.trend (fixed) 7.716e-06 nan nan nan nan nan
sigma2.seasonal 0.0924 0.007 12.672 0.000 0.078 0.107
===================================================================================
Ljung-Box (L1) (Q): 459.85 Jarque-Bera (JB): 38.49
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 2.44 Skew: 0.30
Prob(H) (two-sided): 0.00 Kurtosis: 4.19
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
为了比较，我们构建了不受约束的最大似然估计 (MLE)。在这种情况下，水平的估计将不再对应于 HP 滤波器概念。
[11]:
res_unrestricted = mod.fit()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 4 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 3.63596D+00 |proj g|= 1.07339D-01
This problem is unconstrained.
At iterate 5 f= 2.03169D+00 |proj g|= 4.05225D-01
ys=-5.696E-01 -gs= 2.818E-01 BFGS update SKIPPED
At iterate 10 f= 1.59907D+00 |proj g|= 7.62230D-01
At iterate 15 f= 1.44540D+00 |proj g|= 2.77893D-01
At iterate 20 f= 1.39111D+00 |proj g|= 1.56723D-01
At iterate 25 f= 1.38688D+00 |proj g|= 1.41002D-03
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
4 28 58 1 1 0 2.548D-06 1.387D+00
F = 1.3868826049230436
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
最后，我们可以检索趋势和季节性成分的平滑估计。
[12]:
# Construct the smoothed level estimates
unrestricted_trend = pd.Series(res_unrestricted.level.smoothed, index=endog.index)
restricted_trend = pd.Series(res_restricted.level.smoothed, index=endog.index)
# Construct the smoothed estimates of the seasonal pattern
unrestricted_seasonal = pd.Series(res_unrestricted.seasonal.smoothed, index=endog.index)
restricted_seasonal = pd.Series(res_restricted.seasonal.smoothed, index=endog.index)
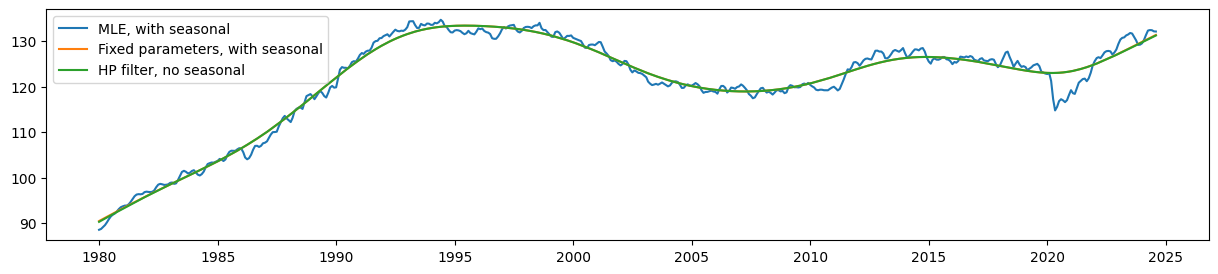
比较估计的水平，很明显，具有固定参数的季节性 UCM 仍然产生一个趋势，该趋势非常接近（虽然不再完全相同）HP 滤波器输出。
同时，来自没有参数限制的模型（MLE 模型）的估计水平比这些水平要平滑得多。
[13]:
fig, ax = plt.subplots(figsize=(15, 3))
ax.plot(unrestricted_trend, label='MLE, with seasonal')
ax.plot(restricted_trend, label='Fixed parameters, with seasonal')
ax.plot(hp_trend, label='HP filter, no seasonal')
ax.legend();
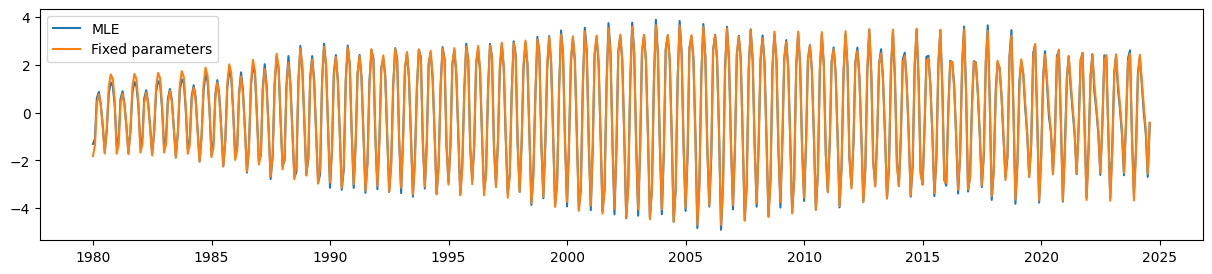
最后，具有参数限制的 UCM 仍然能够很好地捕捉到随时间变化的季节性成分。
[14]:
fig, ax = plt.subplots(figsize=(15, 3))
ax.plot(unrestricted_seasonal, label='MLE')
ax.plot(restricted_seasonal, label='Fixed parameters')
ax.legend();
上次更新：2024 年 10 月 3 日