TVP-VAR、MCMC 和稀疏模拟平滑¶
[1]:
%matplotlib inline
from importlib import reload
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy.stats import invwishart, invgamma
# Get the macro dataset
dta = sm.datasets.macrodata.load_pandas().data
dta.index = pd.date_range('1959Q1', '2009Q3', freq='QS')
背景¶
近年来,通过马尔可夫链蒙特卡罗 (MCMC) 方法对线性高斯状态空间模型进行贝叶斯分析已经变得司空见惯且相对简单,这得益于对给定数据和模型参数的条件下,对未观测状态向量联合后验进行采样的进展(特别是在 Carter 和 Kohn (1994)、de Jong 和 Shephard (1995) 以及 Durbin 和 Koopman (2002) 的研究中)。这对于吉布斯采样 MCMC 方法尤其有用。
虽然这些程序利用了递归卡尔曼滤波器和平滑器的正向/反向应用,但最近的另一项研究采取了不同的方法,并一次性构建了整个状态向量联合后验分布 - 特别是,Chan 和 Jeliazkov (2009) 给出了计量经济学时间序列处理,而 McCausland 等人 (2011) 则进行了更全面的调查。特别是,后验均值和精度矩阵是显式构建的,后者是一个稀疏带状矩阵。然后利用稀疏带状矩阵的 Cholesky 分解的有效算法;这减少了内存成本,并且可以提高性能。根据 McCausland 等人 (2011) 的说法,我们将这种方法称为“Cholesky 因子算法”(CFA)方法。
与基于更典型的卡尔曼滤波器和平滑器 (KFS) 的方法相比,基于 CFA 的模拟平滑器具有一些优点和一些缺点。
CFA 的优点:
联合后验分布的推导相对简单易懂。
在某些情况下,可以比 KFS 方法更快,并且内存占用更少。
在本笔记本末尾的附录中,我们简要讨论了 TVP-VAR 模型中两种模拟平滑器的性能。总而言之:对一台机器进行的简单测试表明,对于 TVP-VAR 模型,Statsmodels 中的 CFA 和 KFS 实现具有大致相同的运行时间,而这两种实现的速度大约是 Chan 和 Jeliazkov (2009) 提供的 Matlab 编写的复制代码的两倍。
CFA 的缺点:
主要缺点是这种方法尚未(至少到目前为止)达到 KFS 方法的普遍性。例如
它不能用于具有观测或状态方程中降秩误差项的模型。
这意味着典型的状态空间模型技巧(即在状态方程中包含恒等式以适应自回归模型中的高阶滞后)不适用。这些模型仍然可以通过 CFA 方法处理,但需要为每个包含的滞后提供略有不同的实现。
例如,将 ARMA 和 VARMA 过程表示为状态空间形式的标准方法确实在观测和/或状态方程中包含恒等式,因此 Chan 和 Jeliazkov (2009) 中给出的基本公式不直接适用于这些模型。
状态初始化/先验中可用的灵活性较低。
在 Statsmodels 中的实现¶
Statsmodels 中已实现了类似于 Chan 和 Jeliazkov (2009) 中给出的基本公式的 CFA 模拟平滑器。
注意:
因此,Statsmodels 中的 CFA 模拟平滑器到目前为止只支持状态转换是真正的阶一马尔可夫过程的情况(即,它不支持使用恒等式叠加成阶一过程的阶 p 马尔可夫过程)。
相比之下,Statsmodels 中的 KFS 平滑器是完全通用的,可用于任何状态空间模型,包括那些具有叠加阶 p 马尔可夫过程或观测和状态方程中其他恒等式的模型。
可以使用 simulation_smoother 方法从状态空间模型构建 KFS 或 CFA 模拟平滑器。为了说明基本原理,我们首先考虑一个简单的例子。
局部水平模型¶
局部水平模型将观测系列 \(y_t\) 分解为一个持久趋势 \(\mu_t\) 和一个瞬态误差分量
该模型满足 CFA 模拟平滑器的要求,因为观测误差项 \(\varepsilon_t\) 和状态创新项 \(\eta_t\) 都是非退化的 - 也就是说,它们的协方差矩阵是满秩的。
我们将此模型应用于通货膨胀,并考虑从联合状态向量的后验中模拟抽取样本。也就是说,我们感兴趣的是从以下内容中进行采样
其中我们定义 \(\mu^t \equiv (\mu_1, \dots, \mu_T)'\) 和 \(y^t \equiv (y_1, \dots, y_T)'\).
在 Statsmodels 中,局部水平模型属于更通用的“未观测分量”模型类别,可以按如下方式构建
[2]:
# Construct a local level model for inflation
mod = sm.tsa.UnobservedComponents(dta.infl, 'llevel')
# Fit the model's parameters (sigma2_varepsilon and sigma2_eta)
# via maximum likelihood
res = mod.fit()
print(res.params)
# Create simulation smoother objects
sim_kfs = mod.simulation_smoother() # default method is KFS
sim_cfa = mod.simulation_smoother(method='cfa') # can specify CFA method
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 2 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.40814D+00 |proj g|= 1.27979D-01
At iterate 5 f= 2.24982D+00 |proj g|= 9.50561D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
2 7 9 1 0 0 2.953D-07 2.250D+00
F = 2.2498167187365663
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
sigma2.irregular 3.373368
sigma2.level 0.744712
dtype: float64
This problem is unconstrained.
模拟平滑器对象 sim_kfs 和 sim_cfa 具有 simulate 方法,用于执行模拟平滑。每次调用 simulate 时,simulated_state 属性将使用从后验中抽取的新的模拟样本重新填充。
下面,我们使用 KFS 和 CFA 方法构建了趋势的 20 个模拟路径,其中模拟是在最大似然参数估计处进行的。
[3]:
nsimulations = 20
simulated_state_kfs = pd.DataFrame(
np.zeros((mod.nobs, nsimulations)), index=dta.index)
simulated_state_cfa = pd.DataFrame(
np.zeros((mod.nobs, nsimulations)), index=dta.index)
for i in range(nsimulations):
# Apply KFS simulation smoothing
sim_kfs.simulate()
# Save the KFS simulated state
simulated_state_kfs.iloc[:, i] = sim_kfs.simulated_state[0]
# Apply CFA simulation smoothing
sim_cfa.simulate()
# Save the CFA simulated state
simulated_state_cfa.iloc[:, i] = sim_cfa.simulated_state[0]
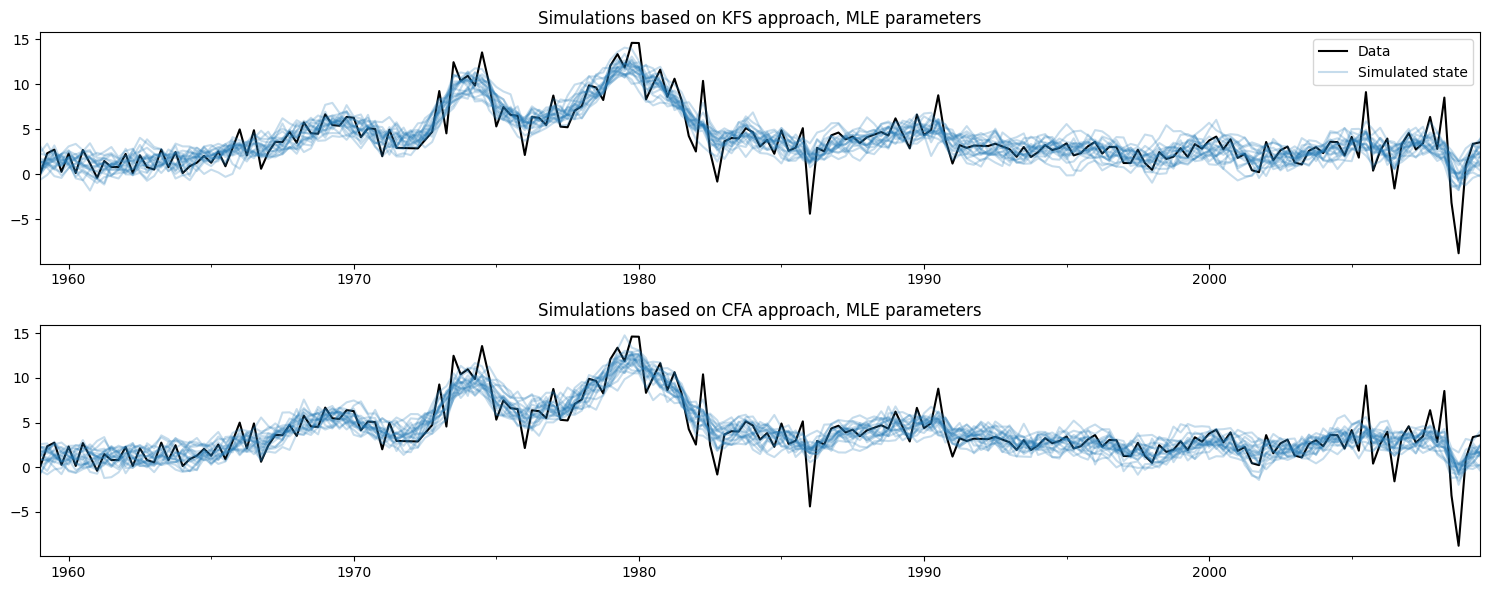
在下面绘制观测数据和使用每种方法创建的模拟,不难看出这两种方法做的事情是一样的。
[4]:
# Plot the inflation data along with simulated trends
fig, axes = plt.subplots(2, figsize=(15, 6))
# Plot data and KFS simulations
dta.infl.plot(ax=axes[0], color='k')
axes[0].set_title('Simulations based on KFS approach, MLE parameters')
simulated_state_kfs.plot(ax=axes[0], color='C0', alpha=0.25, legend=False)
# Plot data and CFA simulations
dta.infl.plot(ax=axes[1], color='k')
axes[1].set_title('Simulations based on CFA approach, MLE parameters')
simulated_state_cfa.plot(ax=axes[1], color='C0', alpha=0.25, legend=False)
# Add a legend, clean up layout
handles, labels = axes[0].get_legend_handles_labels()
axes[0].legend(handles[:2], ['Data', 'Simulated state'])
fig.tight_layout();
更新模型的参数¶
模拟平滑器与模型实例(此处为变量 mod)绑定。只要使用新参数更新模型实例,模拟平滑器就会在将来对 simulate 方法的调用中考虑这些新参数。
这对 MCMC 算法很方便,MCMC 算法反复地 (a) 更新模型参数,(b) 抽取状态向量的样本,然后 (c) 抽取模型参数的新值。
这里我们将模型更改为不同的参数化,从而产生更平滑的趋势,并展示模拟值如何变化(为了简洁,我们只显示了来自 KFS 方法的模拟,但来自 CFA 方法的模拟将是相同的)。
[5]:
fig, ax = plt.subplots(figsize=(15, 3))
# Update the model's parameterization to one that attributes more
# variation in inflation to the observation error and so has less
# variation in the trend component
mod.update([4, 0.05])
# Plot simulations
for i in range(nsimulations):
sim_kfs.simulate()
ax.plot(dta.index, sim_kfs.simulated_state[0],
color='C0', alpha=0.25, label='Simulated state')
# Plot data
dta.infl.plot(ax=ax, color='k', label='Data', zorder=-1)
# Add title, legend, clean up layout
ax.set_title('Simulations with alternative parameterization yielding a smoother trend')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[-2:], labels[-2:])
fig.tight_layout();

应用:通过 MCMC 对 TVP-VAR 模型进行贝叶斯分析¶
Chan 和 Jeliazkov (2009) 考虑的一个应用是通过贝叶斯吉布斯采样 (MCMC) 方法估计的时变参数向量自回归 (TVP-VAR) 模型。他们将此应用于对四个宏观经济时间序列的共同运动进行建模
实际 GDP 增长
通货膨胀
失业率
短期利率
我们将复制他们的示例,使用 Statsmodels 中包含的非常相似的 dataset。
[6]:
# Subset to the four variables of interest
y = dta[['realgdp', 'cpi', 'unemp', 'tbilrate']].copy()
y.columns = ['gdp', 'inf', 'unemp', 'int']
# Convert to real GDP growth and CPI inflation rates
y[['gdp', 'inf']] = np.log(y[['gdp', 'inf']]).diff() * 100
y = y.iloc[1:]
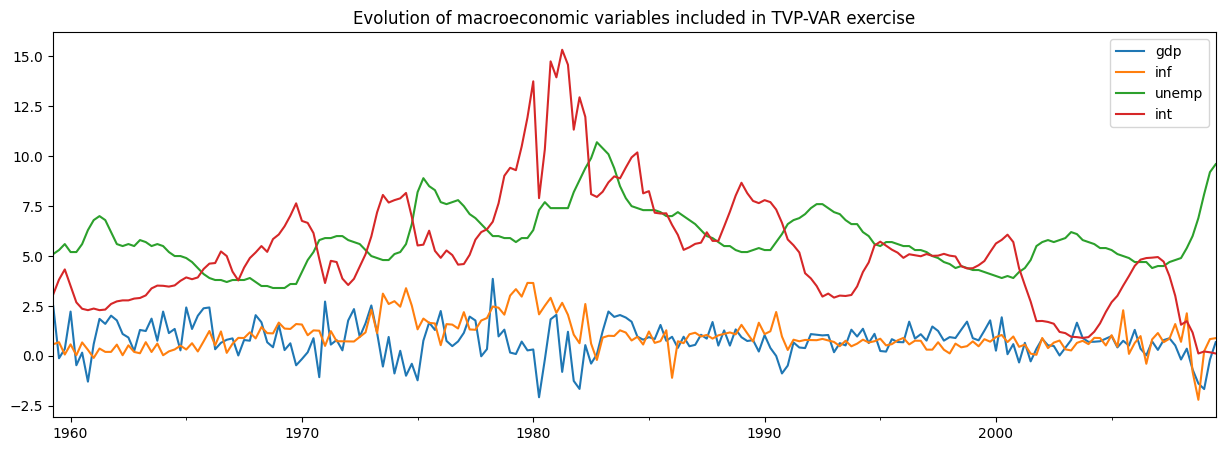
fig, ax = plt.subplots(figsize=(15, 5))
y.plot(ax=ax)
ax.set_title('Evolution of macroeconomic variables included in TVP-VAR exercise');
TVP-VAR 模型¶
注意:本节基于 Chan 和 Jeliazkov (2009) 的第 3.1 节,可以参考该节以获取更多详细信息。
通常(时间不变)VAR(1) 模型通常写成
其中 \(y_t\) 是在时间 \(t\) 观测到的 \(p \times 1\) 变量向量,\(H\) 是协方差矩阵。
TVP-VAR(1) 模型对它进行了推广,允许系数随时间变化。根据 \(\alpha_t = \text{vec}([\mu_t : \Phi_t])\) 将所有参数堆叠成一个向量,其中 \(\text{vec}\) 表示将矩阵的列堆叠成向量的操作,我们根据以下公式对它们随时间的演化进行建模
换句话说,每个参数都根据随机游走独立演化。
请注意,\(\mu_t\) 中有 \(p\) 个系数,\(\Phi_t\) 中有 \(p^2\) 个系数,因此完整的状态向量 \(\alpha\) 的形状为 \(p * (p + 1) \times 1\).
将 TVP-VAR(1) 模型转换为状态空间形式相对简单,实际上我们只需要将观测方程重新写成 SUR 形式即可
其中
只要 \(H\) 满秩且每个方差 \(\sigma_i^2\) 不为零,该模型就满足 CFA 仿真平滑器的要求。
我们还需要为初始状态 \(\alpha_1\) 指定初始化/先验。这里我们将遵循 Chan 和 Jeliazkov (2009) 的方法,使用 \(\alpha_1 \sim N(0, 5 I)\),尽管我们也可以将其建模为弥散的。
除了时变系数 \(\alpha_t\) 外,我们还需要估计的其他参数是协方差矩阵 \(H\) 中的项和随机游走方差 \(\sigma_i^2\)。
Statsmodels 中的 TVP-VAR 模型¶
在 Statsmodels 中以编程方式构建此模型也比较简单,因为基本上有四个步骤
创建一个新的
TVPVAR类作为sm.tsa.statespace.MLEModel的子类填写状态空间系统矩阵的固定值
指定 \(\alpha_1\) 的初始化
创建一个方法,使用协方差矩阵 \(H\) 和随机游走方差 \(\sigma_i^2\) 的新值来更新状态空间系统矩阵。
为此,首先要注意 Statsmodels 使用的通用状态空间表示是
然后 TVP-VAR(1) 模型意味着以下专门化
截距项为零,即 \(c_t = d_t = 0\)
设计矩阵 \(Z_t\) 是时变的,但其值是固定的,如上所述(即,其值包含 1 和 \(y_t\) 的滞后值)
观测协方差矩阵不是时变的,即 \(H_t = H_{t+1} = H\)
转移矩阵不是时变的,并且等于单位矩阵,即 \(T_t = T_{t+1} = I\)
选择矩阵 \(R_t\) 不是时变的,并且也等于单位矩阵,即 \(R_t = R_{t+1} = I\)
状态协方差矩阵 \(Q_t\) 不是时变的,并且是对角线的,即 \(Q_t = Q_{t+1} = \text{diag}(\{\sigma_i^2\})\)
[7]:
# 1. Create a new TVPVAR class as a subclass of sm.tsa.statespace.MLEModel
class TVPVAR(sm.tsa.statespace.MLEModel):
# Steps 2-3 are best done in the class "constructor", i.e. the __init__ method
def __init__(self, y):
# Create a matrix with [y_t' : y_{t-1}'] for t = 2, ..., T
augmented = sm.tsa.lagmat(y, 1, trim='both', original='in', use_pandas=True)
# Separate into y_t and z_t = [1 : y_{t-1}']
p = y.shape[1]
y_t = augmented.iloc[:, :p]
z_t = sm.add_constant(augmented.iloc[:, p:])
# Recall that the length of the state vector is p * (p + 1)
k_states = p * (p + 1)
super().__init__(y_t, exog=z_t, k_states=k_states)
# Note that the state space system matrices default to contain zeros,
# so we don't need to explicitly set c_t = d_t = 0.
# Construct the design matrix Z_t
# Notes:
# -> self.k_endog = p is the dimension of the observed vector
# -> self.k_states = p * (p + 1) is the dimension of the observed vector
# -> self.nobs = T is the number of observations in y_t
self['design'] = np.zeros((self.k_endog, self.k_states, self.nobs))
for i in range(self.k_endog):
start = i * (self.k_endog + 1)
end = start + self.k_endog + 1
self['design', i, start:end, :] = z_t.T
# Construct the transition matrix T = I
self['transition'] = np.eye(k_states)
# Construct the selection matrix R = I
self['selection'] = np.eye(k_states)
# Step 3: Initialize the state vector as alpha_1 ~ N(0, 5I)
self.ssm.initialize('known', stationary_cov=5 * np.eye(self.k_states))
# Step 4. Create a method that we can call to update H and Q
def update_variances(self, obs_cov, state_cov_diag):
self['obs_cov'] = obs_cov
self['state_cov'] = np.diag(state_cov_diag)
# Finally, it can be convenient to define human-readable names for
# each element of the state vector. These will be available in output
@property
def state_names(self):
state_names = np.empty((self.k_endog, self.k_endog + 1), dtype=object)
for i in range(self.k_endog):
endog_name = self.endog_names[i]
state_names[i] = (
['intercept.%s' % endog_name] +
['L1.%s->%s' % (other_name, endog_name) for other_name in self.endog_names])
return state_names.ravel().tolist()
上述类为任何给定数据集定义了状态空间模型。现在我们需要使用之前创建的包含实际 GDP 增长、通货膨胀、失业率和利率的数据集创建它的特定实例。
[8]:
# Create an instance of our TVPVAR class with our observed dataset y
mod = TVPVAR(y)
使用 H、Q 中的临时参数进行初步调查¶
在下面的分析中,我们需要从一些初始参数化开始我们的 MCMC 迭代。遵循 Chan 和 Jeliazkov (2009) 的方法,我们将设置 \(H\) 为数据集的样本协方差矩阵,并将设置 \(\sigma_i^2 = 0.01\) 对于每个 \(i\)。
在讨论允许我们对模型进行推断的 MCMC 方案之前,首先我们可以考虑在简单地插入这些初始参数时模型的输出。为了填写这些参数,我们使用之前定义的 update_variances 方法,然后执行以这些参数为条件的卡尔曼滤波和平滑。
警告:此练习仅作为解释 - 我们必须等待 MCMC 练习的输出,以有意义的方式研究模型的实际含义.
[9]:
initial_obs_cov = np.cov(y.T)
initial_state_cov_diag = [0.01] * mod.k_states
# Update H and Q
mod.update_variances(initial_obs_cov, initial_state_cov_diag)
# Perform Kalman filtering and smoothing
# (the [] is just an empty list that in some models might contain
# additional parameters. Here, we don't have any additional parameters
# so we just pass an empty list)
initial_res = mod.smooth([])
initial_res 变量包含卡尔曼滤波和平滑的输出,以这些初始参数为条件。特别是,我们可能对“平滑状态”感兴趣,即 \(E[\alpha_t \mid y^t, H, \{\sigma_i^2\}]\)。
首先,让我们创建一个函数,该函数随时间绘制系数,并将其分成观察变量方程式的方程。
[10]:
def plot_coefficients_by_equation(states):
fig, axes = plt.subplots(2, 2, figsize=(15, 8))
# The way we defined Z_t implies that the first 5 elements of the
# state vector correspond to the first variable in y_t, which is GDP growth
ax = axes[0, 0]
states.iloc[:, :5].plot(ax=ax)
ax.set_title('GDP growth')
ax.legend()
# The next 5 elements correspond to inflation
ax = axes[0, 1]
states.iloc[:, 5:10].plot(ax=ax)
ax.set_title('Inflation rate')
ax.legend();
# The next 5 elements correspond to unemployment
ax = axes[1, 0]
states.iloc[:, 10:15].plot(ax=ax)
ax.set_title('Unemployment equation')
ax.legend()
# The last 5 elements correspond to the interest rate
ax = axes[1, 1]
states.iloc[:, 15:20].plot(ax=ax)
ax.set_title('Interest rate equation')
ax.legend();
return ax
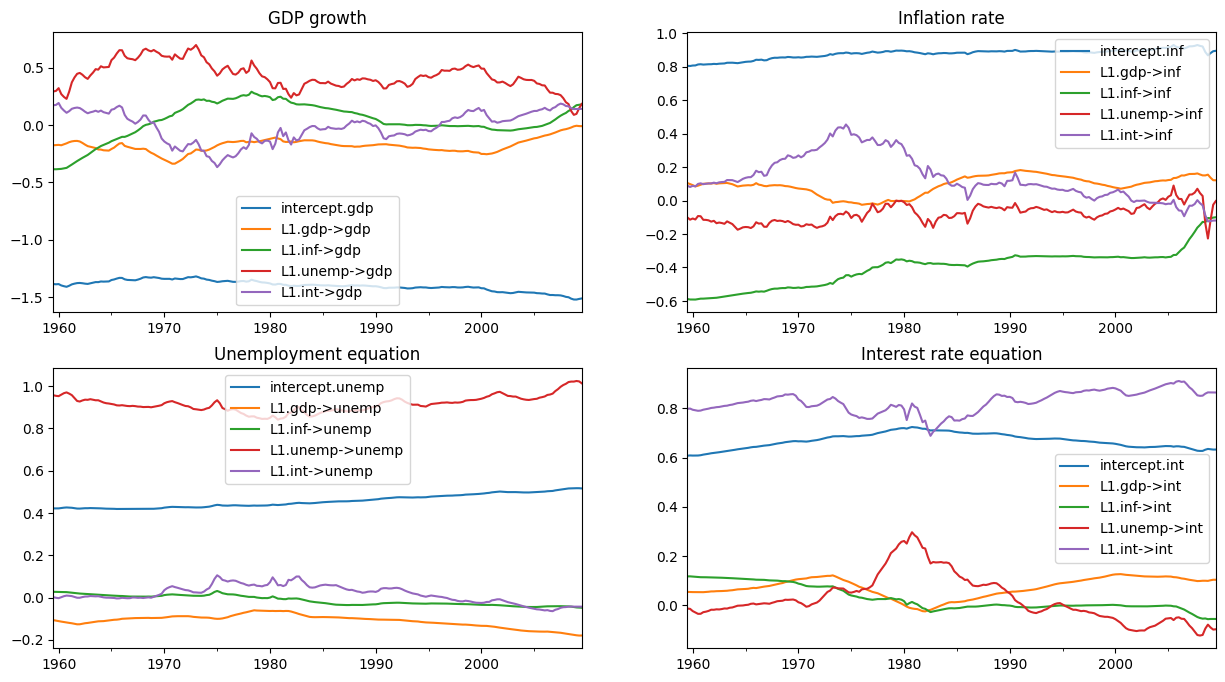
现在,我们对平滑状态感兴趣,这些状态在我们结果对象 initial_res 的 states.smoothed 属性中可用。
如下图所示,初始参数化意味着某些系数存在大量的时间变化。
[11]:
# Here, for illustration purposes only, we plot the time-varying
# coefficients conditional on an ad-hoc parameterization
# Recall that `initial_res` contains the Kalman filtering and smoothing,
# and the `states.smoothed` attribute contains the smoothed states
plot_coefficients_by_equation(initial_res.states.smoothed);
通过 MCMC 进行贝叶斯估计¶
我们现在将实现 Chan 和 Jeliazkov (2009) 中算法 2 中描述的吉布斯采样方案。
我们使用以下(条件共轭)先验
其中 \(\mathcal{IW}\) 表示逆 Wishart 分布,\(\mathcal{IG}\) 表示逆 Gamma 分布。我们将先验超参数设置为
[12]:
# Prior hyperparameters
# Prior for obs. cov. is inverse-Wishart(v_1^0=k + 3, S10=I)
v10 = mod.k_endog + 3
S10 = np.eye(mod.k_endog)
# Prior for state cov. variances is inverse-Gamma(v_{i2}^0 / 2 = 3, S+{i2}^0 / 2 = 0.005)
vi20 = 6
Si20 = 0.01
在运行 MCMC 迭代之前,还有几个实际步骤
创建数组以存储状态向量、观测协方差矩阵和状态误差方差的抽取。
将 H 和 Q 的初始值(如上所述)放入存储向量中
构造与
TVPVAR实例关联的仿真平滑器对象,以抽取状态向量
[13]:
# Gibbs sampler setup
niter = 11000
nburn = 1000
# 1. Create storage arrays
store_states = np.zeros((niter + 1, mod.nobs, mod.k_states))
store_obs_cov = np.zeros((niter + 1, mod.k_endog, mod.k_endog))
store_state_cov = np.zeros((niter + 1, mod.k_states))
# 2. Put in the initial values
store_obs_cov[0] = initial_obs_cov
store_state_cov[0] = initial_state_cov_diag
mod.update_variances(store_obs_cov[0], store_state_cov[0])
# 3. Construct posterior samplers
sim = mod.simulation_smoother(method='cfa')
如前所述,我们可以使用基于卡尔曼滤波和平滑器的仿真平滑器或基于 Cholesky 因子算法的仿真平滑器。
[14]:
for i in range(niter):
mod.update_variances(store_obs_cov[i], store_state_cov[i])
sim.simulate()
# 1. Sample states
store_states[i + 1] = sim.simulated_state.T
# 2. Simulate obs cov
fitted = np.matmul(mod['design'].transpose(2, 0, 1), store_states[i + 1][..., None])[..., 0]
resid = mod.endog - fitted
store_obs_cov[i + 1] = invwishart.rvs(v10 + mod.nobs, S10 + resid.T @ resid)
# 3. Simulate state cov variances
resid = store_states[i + 1, 1:] - store_states[i + 1, :-1]
sse = np.sum(resid**2, axis=0)
for j in range(mod.k_states):
rv = invgamma.rvs((vi20 + mod.nobs - 1) / 2, scale=(Si20 + sse[j]) / 2)
store_state_cov[i + 1, j] = rv
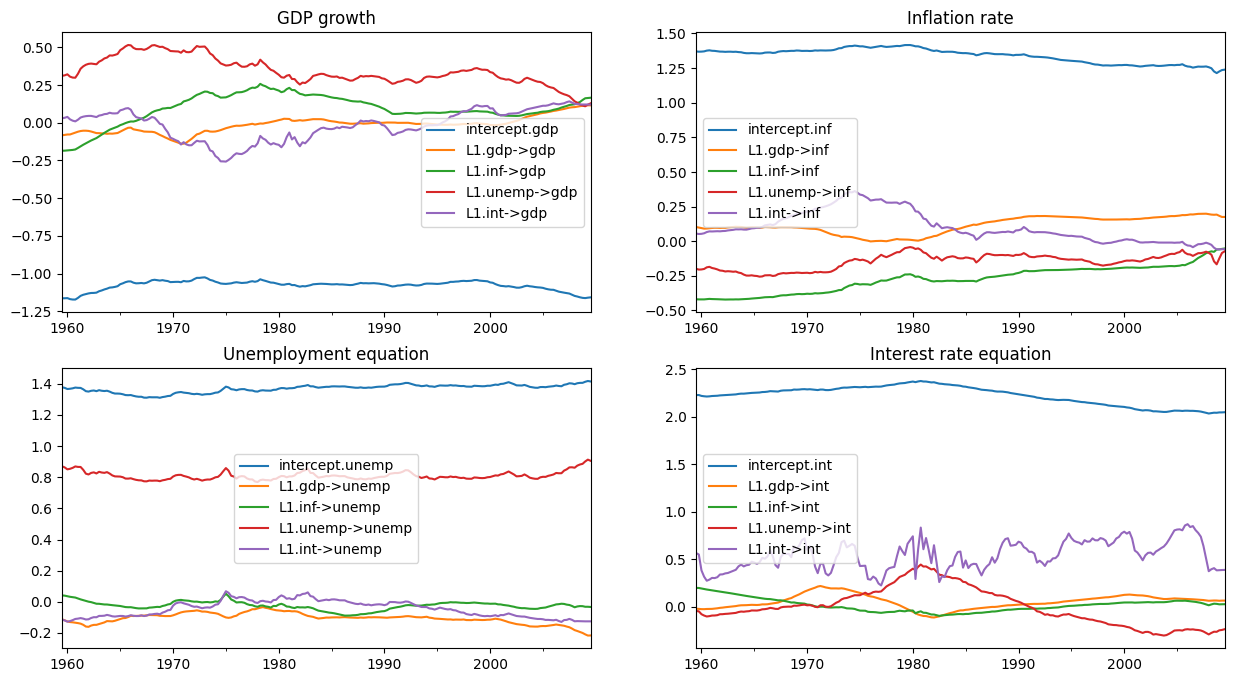
删除一些初始抽取后,后验的剩余抽取允许我们进行推断。下面,我们绘制时变回归系数的后验均值。
(注意:这些图与 Chan 和 Jeliazkov (2009) 发布版本中的图 1 不同,但与在 http://joshuachan.org/code/code_TVPVAR.html 可用的 Matlab 复制代码中生成的图非常相似)
[15]:
# Collect the posterior means of each time-varying coefficient
states_posterior_mean = pd.DataFrame(
np.mean(store_states[nburn + 1:], axis=0),
index=mod._index, columns=mod.state_names)
# Plot these means over time
plot_coefficients_by_equation(states_posterior_mean);
Python 还有一些库可以帮助探索贝叶斯模型。在这里,我们只使用 arviz 包来探索每个协方差和方差参数的可信区间,尽管它提供了一套更广泛的分析工具。
[16]:
import arviz as az
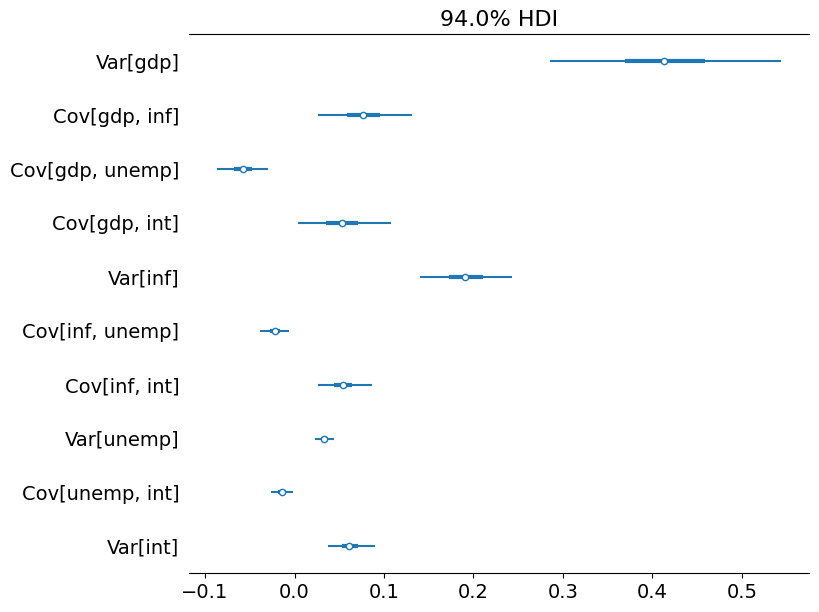
# Collect the observation error covariance parameters
az_obs_cov = az.convert_to_inference_data({
('Var[%s]' % mod.endog_names[i] if i == j else
'Cov[%s, %s]' % (mod.endog_names[i], mod.endog_names[j])):
store_obs_cov[nburn + 1:, i, j]
for i in range(mod.k_endog) for j in range(i, mod.k_endog)})
# Plot the credible intervals
az.plot_forest(az_obs_cov, figsize=(8, 7));
[17]:
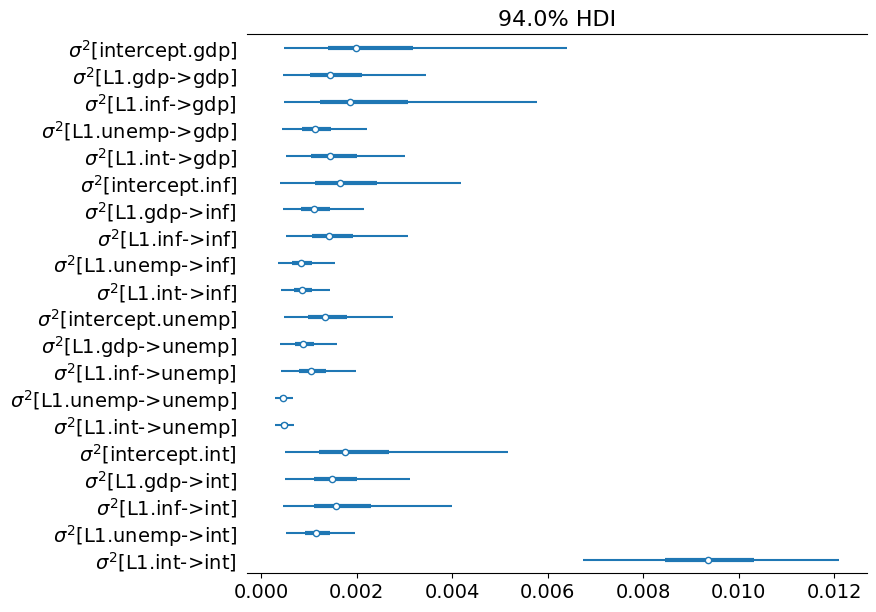
# Collect the state innovation variance parameters
az_state_cov = az.convert_to_inference_data({
r'$\sigma^2$[%s]' % mod.state_names[i]: store_state_cov[nburn + 1:, i]
for i in range(mod.k_states)})
# Plot the credible intervals
az.plot_forest(az_state_cov, figsize=(8, 7));
附录:性能¶
最后,我们运行一些简单的测试,通过使用 %timeit Jupyter 笔记本魔法来比较 KFS 和 CFA 仿真平滑器的性能。
一个警告是,KFS 仿真平滑器可以生成各种输出,而不仅仅是后验状态向量的模拟,并且这些额外的计算可能会使结果产生偏差。为了使结果具有可比性,我们将告诉 KFS 仿真平滑器仅通过使用 simulation_output 参数来计算状态的模拟。
[18]:
from statsmodels.tsa.statespace.simulation_smoother import SIMULATION_STATE
sim_cfa = mod.simulation_smoother(method='cfa')
sim_kfs = mod.simulation_smoother(simulation_output=SIMULATION_STATE)
然后我们可以使用以下代码执行基本的计时练习
%timeit -n 10000 -r 3 sim_cfa.simulate()
%timeit -n 10000 -r 3 sim_kfs.simulate()
在测试过的机器上,这导致了以下结果
2.06 ms ± 26.5 µs per loop (mean ± std. dev. of 3 runs, 10000 loops each)
2.02 ms ± 68.4 µs per loop (mean ± std. dev. of 3 runs, 10000 loops each)
这些结果表明 - 至少对于该模型 - CFA 方法相对于 KFS 方法没有明显的计算收益。但是,这并不排除以下情况
Statsmodels 对 CFA 仿真平滑器的实现可能会进一步优化
CFA 方法可能只在某些模型中显示改进(例如,具有大量
endog变量的模型)
评估第一个可能性的一个简单方法是将 Statsmodels 对 CFA 仿真平滑器的运行时间与 Chan 和 Jeliazkov (2009) 的复制代码(可在 http://joshuachan.org/code/code_TVPVAR.html 获得)中的 Matlab 实现进行比较。
虽然 Statsmodels 版本的 CFA 仿真平滑器是用 Cython 编写的,并编译成 C 代码,但 Matlab 版本利用了 Matlab 的稀疏矩阵功能。因此,即使它不是编译后的代码,我们也可能期望它具有相对良好的性能。
在测试过的机器上,Matlab 版本通常在 70-75 秒内运行 11,000 次迭代的 MCMC 循环,而本笔记本中使用 Statsmodels CFA 仿真平滑器(见上文)的 MCMC 循环,同样是 11,000 次迭代,在 40-45 秒内运行。这证明了 Statsmodels 对 CFA 平滑器的实现已经表现得比较出色(尽管它并不排除可能还有进一步的改进)。
参考文献¶
Carter, Chris K. 和 Robert Kohn。“关于状态空间模型的 Gibbs 采样”。《生物统计学》第 81 卷,第 3 期(1994 年):541-553。
Chan, Joshua CC 和 Ivan Jeliazkov。“状态空间模型中有效的模拟和积分似然估计”。《数学建模与数值优化国际期刊》第 1 卷,第 1-2 期(2009 年):101-120。
De Jong, Piet 和 Neil Shephard。“时间序列模型的仿真平滑器”。《生物统计学》第 82 卷,第 2 期(1995 年):339-350。
Durbin, James 和 Siem Jan Koopman。“用于状态空间时间序列分析的简单高效的仿真平滑器”。《生物统计学》第 89 卷,第 3 期(2002 年):603-616。
McCausland, William J.,Shirley Miller 和 Denis Pelletier。“状态空间模型的仿真平滑:计算效率分析”。《计算统计与数据分析》第 55 卷,第 1 期(2011 年):199-212。