去趋势化、典型特征和商业周期

在影响力很大的文章中，Harvey 和 Jaeger (1993) 描述了使用未观测成分模型（也称为“结构化时间序列模型”）来推导出商业周期的典型特征。

他们的论文开头部分指出

"Establishing the 'stylized facts' associated with a set of time series is widely considered a crucial step
in macroeconomic research ... For such facts to be useful they should (1) be consistent with the stochastic
properties of the data and (2) present meaningful information."

特别是，他们认为，与流行的 Hodrick-Prescott 滤波器或 Box-Jenkins ARIMA 建模技术相比，这些目标通常更适合使用未观测成分方法来实现。

statsmodels 能够执行所有三种类型的分析，下面我们将按照他们论文的步骤进行操作，使用略微更新的数据集。

[1]:

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

from IPython.display import display, Latex

未观测成分

statsmodels 中可用的未观测成分模型可以写成

\[y_t = \underbrace{\mu_{t}}_{\text{trend}} + \underbrace{\gamma_{t}}_{\text{seasonal}} + \underbrace{c_{t}}_{\text{cycle}} + \sum_{j=1}^k \underbrace{\beta_j x_{jt}}_{\text{explanatory}} + \underbrace{\varepsilon_t}_{\text{irregular}}\]

参见 Durbin 和 Koopman 2012，第 3 章了解符号和更多细节。请注意，不同个别成分的不同规范可以支持各种模型。论文和下面考虑的特定模型是这个一般方程的特殊化。

趋势

趋势成分是包含截距和线性时间趋势的回归模型的动态扩展。

\[\begin{split}\begin{align} \underbrace{\mu_{t+1}}_{\text{level}} & = \mu_t + \nu_t + \eta_{t+1} \qquad & \eta_{t+1} \sim N(0, \sigma_\eta^2) \\\\ \underbrace{\nu_{t+1}}_{\text{trend}} & = \nu_t + \zeta_{t+1} & \zeta_{t+1} \sim N(0, \sigma_\zeta^2) \\ \end{align}\end{split}\]

其中，水平是截距项的推广，它可以在时间上动态变化，趋势是时间趋势的推广，使得斜率可以在时间上动态变化。

对于这两个元素（水平和趋势），我们可以考虑以下模型

  • 元素包含与否（如果包含趋势，则必须也包含水平）。

  • 元素是确定性的还是随机的（即误差项的方差是否限于零或不为零）。

通过 MLE 估计的唯一附加参数是任何包含的随机成分的方差。

这导致以下规范

水平

趋势

随机水平

随机趋势

常数

✓

局部水平（随机游走）

✓

✓

确定性趋势

✓

✓

具有确定性趋势的局部水平（带有漂移的随机游走）

✓

✓

✓

局部线性趋势

✓

✓

✓

✓

平滑趋势（积分随机游走）

✓

✓

✓

季节性

季节性成分写成

\[\gamma_t = - \sum_{j=1}^{s-1} \gamma_{t+1-j} + \omega_t \qquad \omega_t \sim N(0, \sigma_\omega^2)\]

周期性（季节数）为 s，其定义特征是（没有误差项），季节性成分在一个完整周期内之和为零。误差项的包含允许季节性效应随着时间的推移而变化。

该模型的变体有

  • 周期性 s

  • 是否将季节性效应设为随机。

如果季节性效应是随机的，那么通过 MLE 估计一个额外参数（误差项的方差）。

周期

周期性成分旨在捕获比季节性成分捕获的时间范围长得多的周期性效应。例如，在经济学中，周期性项通常旨在捕获商业周期，然后预计其周期在“1.5 到 12 年”之间（参见 Durbin 和 Koopman）。

周期写成

\[\begin{split}\begin{align} c_{t+1} & = c_t \cos \lambda_c + c_t^* \sin \lambda_c + \tilde \omega_t \qquad & \tilde \omega_t \sim N(0, \sigma_{\tilde \omega}^2) \\\\ c_{t+1}^* & = -c_t \sin \lambda_c + c_t^* \cos \lambda_c + \tilde \omega_t^* & \tilde \omega_t^* \sim N(0, \sigma_{\tilde \omega}^2) \end{align}\end{split}\]

参数 \(\lambda_c\)（周期的频率）是通过 MLE 估计的额外参数。如果季节性效应是随机的，那么需要估计另一个参数（误差项的方差 - 请注意，这里两个误差项共享相同的方差，但假设具有独立的抽取）。

不规则

不规则成分被假定为白噪声误差项。其方差是通过 MLE 估计的参数；即

\[\varepsilon_t \sim N(0, \sigma_\varepsilon^2)\]

在某些情况下，我们可能希望通过允许自回归效应来推广不规则成分

\[\varepsilon_t = \rho(L) \varepsilon_{t-1} + \epsilon_t, \qquad \epsilon_t \sim N(0, \sigma_\epsilon^2)\]

在这种情况下，自回归参数也将通过 MLE 估计。

回归效应

我们可能希望通过包含附加项来允许解释变量

\[\sum_{j=1}^k \beta_j x_{jt}\]

或通过包含干预效应来允许

\[\begin{split}\begin{align} \delta w_t \qquad \text{where} \qquad w_t & = 0, \qquad t < \tau, \\\\ & = 1, \qquad t \ge \tau \end{align}\end{split}\]

这些附加参数可以通过 MLE 估计，也可以通过将它们作为状态空间公式的组成部分来包含。

数据

按照 Harvey 和 Jaeger 的说法，我们将考虑以下时间序列

  • 美国实际 GNP，“产出”，(GNPC96)

  • 美国 GNP 隐含价格平减指数，“价格”，(GNPDEF)

  • 美国货币基础，“货币”，(AMBSL)

原始论文中时间范围因系列而异，但大体上是 1954-1989 年。下面我们使用所有系列 1948-2008 年期间的数据。虽然未观测成分方法允许在模型内隔离季节性成分，但论文和本文中考虑的系列已经过季节性调整。

这里考虑的所有数据系列都取自 联邦储备经济数据 (FRED)。方便的是，Python 库 Pandas 能够直接从 FRED 下载数据。

[2]:

# Datasets
from pandas_datareader.data import DataReader

# Get the raw data
start = '1948-01'
end = '2008-01'
us_gnp = DataReader('GNPC96', 'fred', start=start, end=end)
us_gnp_deflator = DataReader('GNPDEF', 'fred', start=start, end=end)
us_monetary_base = DataReader('AMBSL', 'fred', start=start, end=end).resample('QS').mean()
recessions = DataReader('USRECQ', 'fred', start=start, end=end).resample('QS').last().values[:,0]

# Construct the dataframe
dta = pd.concat(map(np.log, (us_gnp, us_gnp_deflator, us_monetary_base)), axis=1)
dta.columns = ['US GNP','US Prices','US monetary base']
dta.index.freq = dta.index.inferred_freq
dates = dta.index._mpl_repr()

为了了解这三个变量在时间范围内的变化趋势，我们可以将它们绘制出来

[3]:

# Plot the data
ax = dta.plot(figsize=(13,3))
ylim = ax.get_ylim()
ax.xaxis.grid()
ax.fill_between(dates, ylim[0]+1e-5, ylim[1]-1e-5, recessions, facecolor='k', alpha=0.1);
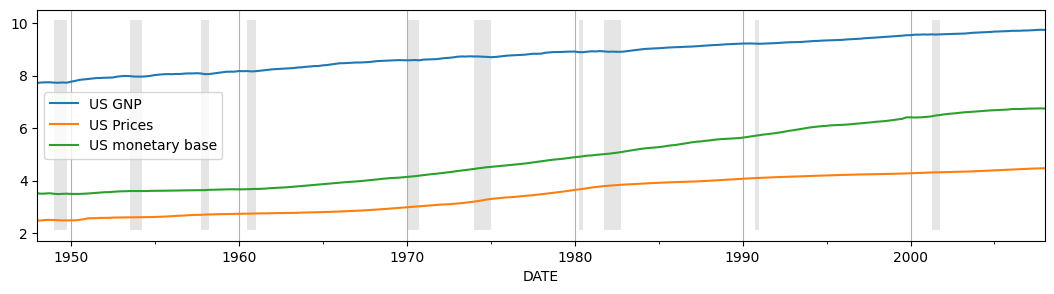
../../../_images/examples_notebooks_generated_statespace_structural_harvey_jaeger_6_0.png

模型

由于数据已经过季节性调整，并且没有明显的解释变量，因此考虑的一般模型是

\[y_t = \underbrace{\mu_{t}}_{\text{trend}} + \underbrace{c_{t}}_{\text{cycle}} + \underbrace{\varepsilon_t}_{\text{irregular}}\]

假设不规则成分为白噪声，周期成分为随机且阻尼的。最终的建模选择是要使用的趋势成分规范。Harvey 和 Jaeger 考虑了两个模型

  1. 局部线性趋势（“无限制”模型）

  2. 平滑趋势（“限制”模型，因为我们强制 \(\sigma_\eta = 0\)）

下面，我们为每种模型类型构建 kwargs 字典。请注意，有两种方法可以指定模型。一种方法是直接指定组件，如上表所示。另一种方法是使用字符串名称，这些名称映射到各种规范。

[4]:

# Model specifications

# Unrestricted model, using string specification
unrestricted_model = {
    'level': 'local linear trend', 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
}

# Unrestricted model, setting components directly
# This is an equivalent, but less convenient, way to specify a
# local linear trend model with a stochastic damped cycle:
# unrestricted_model = {
#     'irregular': True, 'level': True, 'stochastic_level': True, 'trend': True, 'stochastic_trend': True,
#     'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
# }

# The restricted model forces a smooth trend
restricted_model = {
    'level': 'smooth trend', 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
}

# Restricted model, setting components directly
# This is an equivalent, but less convenient, way to specify a
# smooth trend model with a stochastic damped cycle. Notice
# that the difference from the local linear trend model is that
# `stochastic_level=False` here.
# unrestricted_model = {
#     'irregular': True, 'level': True, 'stochastic_level': False, 'trend': True, 'stochastic_trend': True,
#     'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
# }

我们现在拟合以下模型

  1. 产出，无限制模型

  2. 价格，无限制模型

  3. 价格，限制模型

  4. 货币，无限制模型

  5. 货币，限制模型

[5]:

# Output
output_mod = sm.tsa.UnobservedComponents(dta['US GNP'], **unrestricted_model)
output_res = output_mod.fit(method='powell', disp=False)

# Prices
prices_mod = sm.tsa.UnobservedComponents(dta['US Prices'], **unrestricted_model)
prices_res = prices_mod.fit(method='powell', disp=False)

prices_restricted_mod = sm.tsa.UnobservedComponents(dta['US Prices'], **restricted_model)
prices_restricted_res = prices_restricted_mod.fit(method='powell', disp=False)

# Money
money_mod = sm.tsa.UnobservedComponents(dta['US monetary base'], **unrestricted_model)
money_res = money_mod.fit(method='powell', disp=False)

money_restricted_mod = sm.tsa.UnobservedComponents(dta['US monetary base'], **restricted_model)
money_restricted_res = money_restricted_mod.fit(method='powell', disp=False)

一旦我们拟合了这些模型，就可以通过多种方式来显示信息。查看美国 GNP 模型，我们可以使用拟合对象上的 summary 方法来总结模型的拟合情况。

[6]:

print(output_res.summary())

                            Unobserved Components Results
=====================================================================================
Dep. Variable:                        US GNP   No. Observations:                  241
Model:                    local linear trend   Log Likelihood                 769.972
                   + damped stochastic cycle   AIC                          -1527.945
Date:                       Thu, 03 Oct 2024   BIC                          -1507.136
Time:                               15:50:16   HQIC                         -1519.558
Sample:                           01-01-1948
                                - 01-01-2008
Covariance Type:                         opg
====================================================================================
                       coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------------
sigma2.irregular  1.399e-06   7.35e-06      0.190      0.849    -1.3e-05    1.58e-05
sigma2.level      2.775e-06   4.97e-05      0.056      0.955   -9.47e-05       0.000
sigma2.trend      3.199e-06   1.48e-06      2.162      0.031    2.99e-07     6.1e-06
sigma2.cycle      3.871e-05   2.55e-05      1.517      0.129   -1.13e-05    8.87e-05
frequency.cycle      0.4496      0.047      9.548      0.000       0.357       0.542
damping.cycle        0.8672      0.042     20.564      0.000       0.785       0.950
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):                 9.27
Prob(Q):                              1.00   Prob(JB):                         0.01
Heteroskedasticity (H):               0.26   Skew:                            -0.04
Prob(H) (two-sided):                  0.00   Kurtosis:                         3.97
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

对于未观测成分模型，尤其是当探索与引言中第 (2) 点一致的典型特征时，通常更具指导意义的是绘制估计的未观测成分（例如水平、趋势和周期）本身，以查看它们是否提供了对数据的有意义描述。

拟合对象的 plot_components 方法可用于显示每个估计状态的图和置信区间，以及观测数据与模型一步预测的图，以评估拟合情况。

[7]:

fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));

/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/structural.py:1738: RuntimeWarning: invalid value encountered in sqrt
  std_errors = np.sqrt(component_bunch['%s_cov' % which])
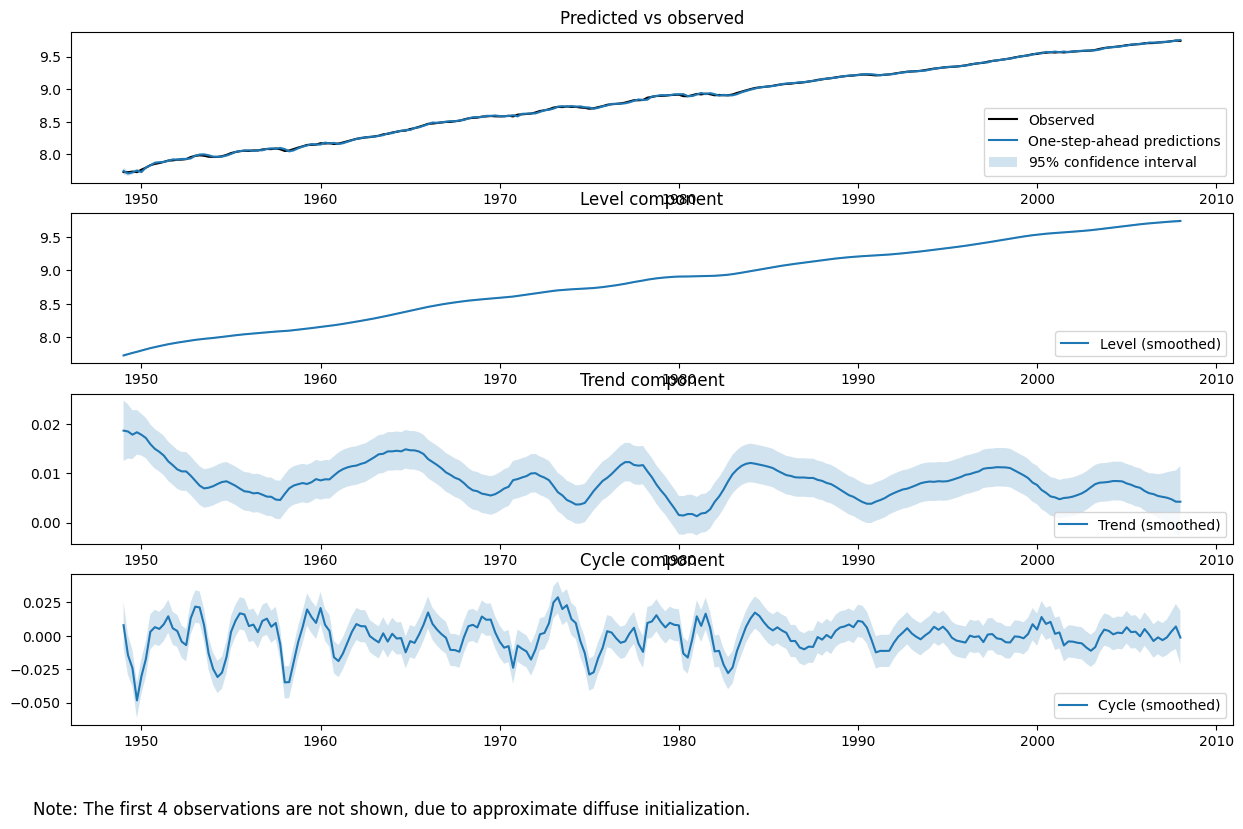
../../../_images/examples_notebooks_generated_statespace_structural_harvey_jaeger_14_1.png

最后，Harvey 和 Jaeger 以另一种方式总结了模型，以突出显示趋势和周期性成分的相对重要性；下面我们复制他们的表格 I。我们找到的值大体上与他们的表格中的值一致，但在细节上有所不同。

[8]:

# Create Table I
table_i = np.zeros((5,6))

start = dta.index[0]
end = dta.index[-1]
time_range = '%d:%d-%d:%d' % (start.year, start.quarter, end.year, end.quarter)
models = [
    ('US GNP', time_range, 'None'),
    ('US Prices', time_range, 'None'),
    ('US Prices', time_range, r'$\sigma_\eta^2 = 0$'),
    ('US monetary base', time_range, 'None'),
    ('US monetary base', time_range, r'$\sigma_\eta^2 = 0$'),
]
index = pd.MultiIndex.from_tuples(models, names=['Series', 'Time range', 'Restrictions'])
parameter_symbols = [
    r'$\sigma_\zeta^2$', r'$\sigma_\eta^2$', r'$\sigma_\kappa^2$', r'$\rho$',
    r'$2 \pi / \lambda_c$', r'$\sigma_\varepsilon^2$',
]

i = 0
for res in (output_res, prices_res, prices_restricted_res, money_res, money_restricted_res):
    if res.model.stochastic_level:
        (sigma_irregular, sigma_level, sigma_trend,
         sigma_cycle, frequency_cycle, damping_cycle) = res.params
    else:
        (sigma_irregular, sigma_level,
         sigma_cycle, frequency_cycle, damping_cycle) = res.params
        sigma_trend = np.nan
    period_cycle = 2 * np.pi / frequency_cycle

    table_i[i, :] = [
        sigma_level*1e7, sigma_trend*1e7,
        sigma_cycle*1e7, damping_cycle, period_cycle,
        sigma_irregular*1e7
    ]
    i += 1

pd.set_option('float_format', lambda x: '%.4g' % np.round(x, 2) if not np.isnan(x) else '-')
table_i = pd.DataFrame(table_i, index=index, columns=parameter_symbols)
table_i

[8]:
$\sigma_\zeta^2$ $\sigma_\eta^2$ $\sigma_\kappa^2$ $\rho$ $2 \pi / \lambda_c$ $\sigma_\varepsilon^2$
系列 时间范围 限制
美国 GNP 1948:1-2008:1 无 27.75 31.99 387.1 0.87 13.98 13.99
美国价格 1948:1-2008:1 无 0 61.88 20.71 0.43 6.55 0
$\sigma_\eta^2 = 0$ 61.92 NaN 20.69 0.43 6.55 0
美国货币基础 1948:1-2008:1 无 68.75 18.86 192.7 0.89 23.19 0
$\sigma_\eta^2 = 0$ 18.92 NaN 247.1 0.89 23.8 0
最后更新：2024 年 10 月 3 日