动态因素和同期指标¶
因子模型通常试图找到少数未观察到的“因素”,这些因素影响着大量观察变量中的大部分变化,并且它们与主成分分析等降维技术相关。动态因子模型明确地对未观察到的因素的转移动力学进行建模,因此通常应用于时间序列数据。
宏观经济同期指标旨在捕捉“商业周期”的共同组成部分;假设这种组成部分会同时影响许多宏观经济变量。虽然同期指数的估计和使用(例如同期经济指标指数)早于动态因子模型,但在几篇有影响力的论文中,Stock 和 Watson (1989, 1991) 使用动态因子模型为其提供了理论基础。
下面,我们遵循 Kim 和 Nelson (1999) 在 Stock 和 Watson (1991) 模型中找到的处理方法,来制定一个动态因子模型,通过最大似然估计其参数,并创建一个同期指数。
宏观经济数据¶
同期指数是通过考虑四个宏观经济变量的共同变动创建的(这些变量的版本可在FRED 上获得;下面使用的系列 ID 在括号中给出)
工业生产 (IPMAN)
实际总收入(不包括转移支付)(W875RX1)
制造业和贸易销售额 (CMRMTSPL)
非农业就业人员 (PAYEMS)
在所有情况下,数据均为月度频率,并且已经过季节性调整;所考虑的时间范围为 1972 年至 2005 年。
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
np.set_printoptions(precision=4, suppress=True, linewidth=120)
[2]:
from pandas_datareader.data import DataReader
# Get the datasets from FRED
start = '1979-01-01'
end = '2014-12-01'
indprod = DataReader('IPMAN', 'fred', start=start, end=end)
income = DataReader('W875RX1', 'fred', start=start, end=end)
sales = DataReader('CMRMTSPL', 'fred', start=start, end=end)
emp = DataReader('PAYEMS', 'fred', start=start, end=end)
# dta = pd.concat((indprod, income, sales, emp), axis=1)
# dta.columns = ['indprod', 'income', 'sales', 'emp']
注意:在 FRED 的最近更新(2015 年 8 月 12 日)中,时间序列 CMRMTSPL 被截断,从 1997 年开始;这可能是由于 CMRMTSPL 是一个拼接序列,因此早期来自系列 HMRMT,而后期由 CMRMT 定义造成的错误。
此后(2016 年 2 月 11 日)已更正,但是该序列也可以通过手动从 HMRMT 和 CMRMT 中构建,如下所示(过程取自 Alfred xls 文件中的说明)。
[3]:
# HMRMT = DataReader('HMRMT', 'fred', start='1967-01-01', end=end)
# CMRMT = DataReader('CMRMT', 'fred', start='1997-01-01', end=end)
[4]:
# HMRMT_growth = HMRMT.diff() / HMRMT.shift()
# sales = pd.Series(np.zeros(emp.shape[0]), index=emp.index)
# # Fill in the recent entries (1997 onwards)
# sales[CMRMT.index] = CMRMT
# # Backfill the previous entries (pre 1997)
# idx = sales.loc[:'1997-01-01'].index
# for t in range(len(idx)-1, 0, -1):
# month = idx[t]
# prev_month = idx[t-1]
# sales.loc[prev_month] = sales.loc[month] / (1 + HMRMT_growth.loc[prev_month].values)
[5]:
dta = pd.concat((indprod, income, sales, emp), axis=1)
dta.columns = ['indprod', 'income', 'sales', 'emp']
dta.index.freq = dta.index.inferred_freq
[6]:
dta.loc[:, 'indprod':'emp'].plot(subplots=True, layout=(2, 2), figsize=(15, 6));
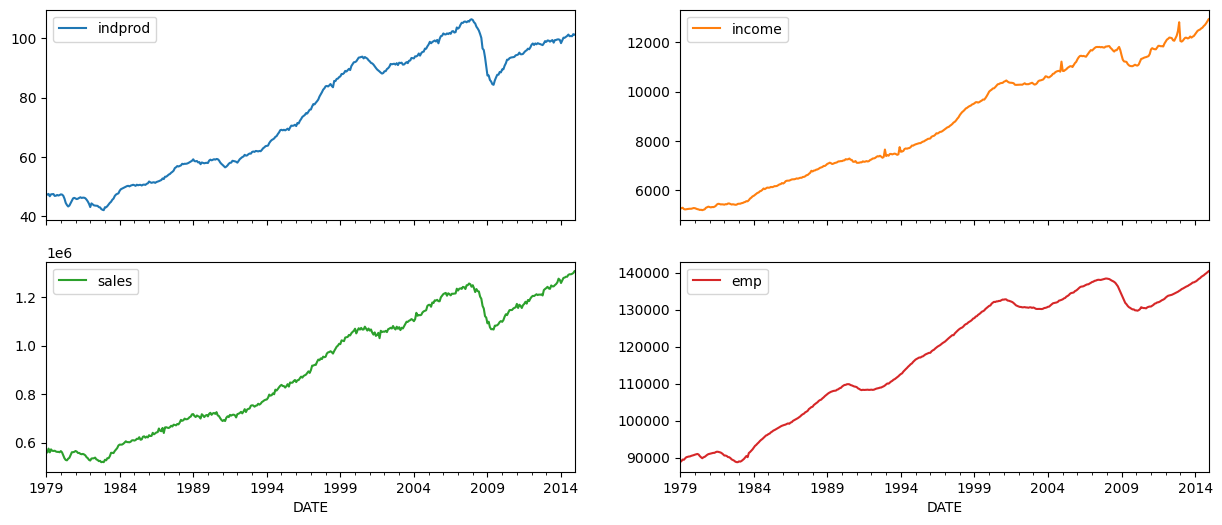
Stock 和 Watson (1991) 报告说,对于他们的数据集,他们无法拒绝每个序列中存在单位根的零假设(因此序列是集成的),但他们没有发现强有力证据表明序列是协整的。
因此,他们建议使用变量的第一差分(对数)进行模型估计,这些差分经过去均值和标准化。
[7]:
# Create log-differenced series
dta['dln_indprod'] = (np.log(dta.indprod)).diff() * 100
dta['dln_income'] = (np.log(dta.income)).diff() * 100
dta['dln_sales'] = (np.log(dta.sales)).diff() * 100
dta['dln_emp'] = (np.log(dta.emp)).diff() * 100
# De-mean and standardize
dta['std_indprod'] = (dta['dln_indprod'] - dta['dln_indprod'].mean()) / dta['dln_indprod'].std()
dta['std_income'] = (dta['dln_income'] - dta['dln_income'].mean()) / dta['dln_income'].std()
dta['std_sales'] = (dta['dln_sales'] - dta['dln_sales'].mean()) / dta['dln_sales'].std()
dta['std_emp'] = (dta['dln_emp'] - dta['dln_emp'].mean()) / dta['dln_emp'].std()
动态因素¶
一般动态因子模型写成
其中 \(y_t\) 是观察到的数据,\(f_t\) 是未观察到的因素(作为向量自回归演化),\(x_t\) 是(可选的)外生变量,而 \(u_t\) 是误差或“特性”过程(\(u_t\) 也可选地允许自相关)。\(\Lambda\) 矩阵通常被称为“因素载荷”矩阵。因素误差项的方差被设置为单位矩阵以确保未观察到的因素的识别。
该模型可以转换为状态空间形式,并且可以通过卡尔曼滤波器估计未观察到的因素。似然可以作为滤波递归的副产品进行评估,并且可以使用最大似然估计来估计参数。
模型规范¶
此应用程序中的特定动态因子模型具有 1 个未观察到的因素,该因素被假定为遵循 AR(2) 过程。创新 \(\varepsilon_t\) 被假定为独立的(因此 \(\Sigma\) 是一个对角矩阵),并且与每个方程相关的误差项 \(u_{i,t}\) 被假定为遵循独立的 AR(2) 过程。
因此,这里考虑的规范是
其中 \(i\) 是以下之一:[indprod, income, sales, emp ]。
此模型可以使用 statsmodels 中内置的 DynamicFactor 模型来制定。特别是,我们有以下规范
k_factors = 1- (有 1 个未观察到的因素)factor_order = 2- (它遵循 AR(2) 过程)error_var = False- (误差作为独立的 AR 过程而不是作为 VAR 共同演化 - 请注意,这是默认选项,因此在下面未指定)error_order = 2- (误差为 2 阶自相关:即 AR(2) 过程)error_cov_type = 'diagonal'- (创新不相关;这也是默认值)
创建模型后,可以通过最大似然估计参数;这是使用 fit() 方法完成的。
注意:请记住我们已经对数据进行了去均值和标准化;这对于解释以下结果很重要。
旁注:在他们的经验示例中,Kim 和 Nelson (1999) 实际上考虑了一个略有不同的模型,其中允许就业变量也依赖于因素的滞后值 - 此模型不适合内置的 DynamicFactor 类,但可以通过使用子类来实现所需的新的参数和限制来适应 - 请参见下面的附录 A。
参数估计¶
多元模型可能具有相对较多的参数,并且可能难以从局部最小值中逃逸以找到最大似然。为了尽量减少这个问题,我使用 Scipy 中可用的修改后的 Powell 方法执行初始最大化步骤(从模型定义的起始参数开始)(有关更多信息,请参阅最小化文档)。然后将生成的参数用作标准 LBFGS 优化方法的起始参数。
[8]:
# Get the endogenous data
endog = dta.loc['1979-02-01':, 'std_indprod':'std_emp']
# Create the model
mod = sm.tsa.DynamicFactor(endog, k_factors=1, factor_order=2, error_order=2)
initial_res = mod.fit(method='powell', disp=False)
res = mod.fit(initial_res.params, disp=False)
估计值¶
模型估计后,我们可以使用两个组件进行分析或推断
估计的参数
估计的因素
参数¶
估计的参数有助于理解模型的含义,尽管在具有更多观察变量和/或未观察因素的模型中,它们可能难以解释。
这种困难的一个原因是由于因素载荷和未观察到的因素之间的识别问题。一个容易看到的识别问题是载荷和因素的符号:与下面显示的模型等效的模型将来自反转所有因素载荷和未观察到的因素的符号。
在这里,此模型中一个易于解释的含义是未观察到的因素的持久性:我们发现它表现出相当大的持久性。
[9]:
print(res.summary(separate_params=False))
Statespace Model Results
=================================================================================================================
Dep. Variable: ['std_indprod', 'std_income', 'std_sales', 'std_emp'] No. Observations: 431
Model: DynamicFactor(factors=1, order=2) Log Likelihood -1586.566
+ AR(2) errors AIC 3209.133
Date: Thu, 03 Oct 2024 BIC 3282.323
Time: 16:05:06 HQIC 3238.031
Sample: 02-01-1979
- 12-01-2014
Covariance Type: opg
====================================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------------------------
loading.f1.std_indprod 0.5044 0.007 70.635 0.000 0.490 0.518
loading.f1.std_income 0.2313 0.021 10.956 0.000 0.190 0.273
loading.f1.std_sales 0.2707 0.020 13.249 0.000 0.231 0.311
loading.f1.std_emp 0.6354 0.011 56.890 0.000 0.613 0.657
sigma2.std_indprod 0.0023 3.89e-05 59.178 0.000 0.002 0.002
sigma2.std_income 0.8423 0.022 37.629 0.000 0.798 0.886
sigma2.std_sales 0.7672 0.053 14.516 0.000 0.664 0.871
sigma2.std_emp 0.0553 0.001 91.451 0.000 0.054 0.056
L1.f1.f1 0.3455 0.024 14.605 0.000 0.299 0.392
L2.f1.f1 0.4471 0.025 17.718 0.000 0.398 0.497
L1.e(std_indprod).e(std_indprod) -1.9726 0.001 -3312.592 0.000 -1.974 -1.971
L2.e(std_indprod).e(std_indprod) -1.0000 2.82e-06 -3.54e+05 0.000 -1.000 -1.000
L1.e(std_income).e(std_income) -0.2412 0.019 -12.760 0.000 -0.278 -0.204
L2.e(std_income).e(std_income) -0.1400 0.033 -4.202 0.000 -0.205 -0.075
L1.e(std_sales).e(std_sales) -0.3118 0.043 -7.299 0.000 -0.396 -0.228
L2.e(std_sales).e(std_sales) -0.0287 0.030 -0.958 0.338 -0.088 0.030
L1.e(std_emp).e(std_emp) 0.3580 0.009 40.009 0.000 0.340 0.376
L2.e(std_emp).e(std_emp) 0.4870 0.010 50.717 0.000 0.468 0.506
================================================================================================
Ljung-Box (L1) (Q): nan, 0.15, 0.62, 6.97 Jarque-Bera (JB): nan, 10067.99, 9.30, 4015.88
Prob(Q): nan, 0.70, 0.43, 0.01 Prob(JB): nan, 0.00, 0.01, 0.00
Heteroskedasticity (H): nan, 4.25, 0.50, 0.37 Skew: nan, -0.91, 0.02, 1.12
Prob(H) (two-sided): nan, 0.00, 0.00, 0.00 Kurtosis: nan, 26.61, 3.72, 17.79
================================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/stattools.py:1431: RuntimeWarning: invalid value encountered in divide
test_statistic = numer_squared_sum / denom_squared_sum
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/stattools.py:702: RuntimeWarning: invalid value encountered in divide
acf = avf[: nlags + 1] / avf[0]
估计的因素¶
虽然绘制未观察到的因素可能很有用,但在这里可能不如人们想象的那样有用,原因有两个
上面描述的与符号相关的识别问题。
由于数据已差分,因此估计的因素解释了差分数据的变化,而不是原始数据的变化。
正是出于这些原因,创建了同期指数(见下文)。
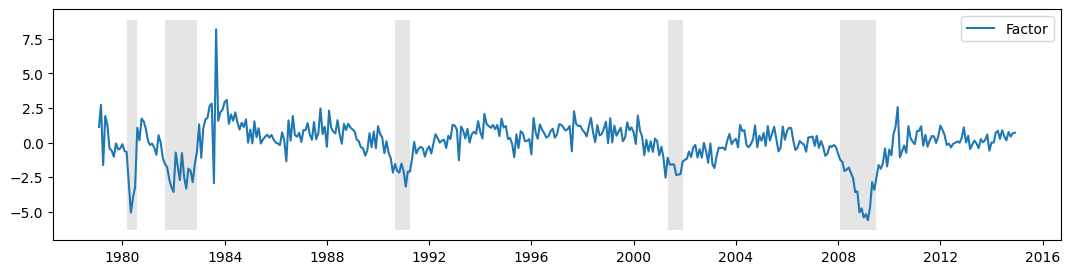
考虑到这些保留意见,下面绘制了未观察到的因素,以及美国经济衰退的 NBER 指标。该因素似乎成功地捕捉到了一些商业周期活动。
[10]:
fig, ax = plt.subplots(figsize=(13,3))
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, res.factors.filtered[0], label='Factor')
ax.legend()
# Retrieve and also plot the NBER recession indicators
rec = DataReader('USREC', 'fred', start=start, end=end)
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
估计后¶
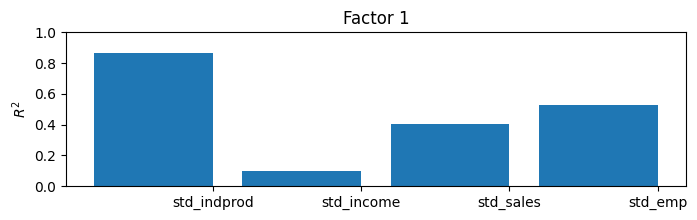
虽然这里我们将能够通过构建同期指数来解释模型的结果,但有一种有用且通用的方法可以了解估计的因素所捕捉到的内容。通过将估计的因素视为已知,将它们(以及一个常数)分别(一次一个)回归到每个观察到的变量上,并记录决定系数(\(R^2\) 值),我们可以了解每个因素解释了大部分方差的变量以及它没有解释的变量。
在具有更多变量和更多因素的模型中,这有时可以赋予因素意义(例如,有时一个因素将主要加载到实际变量上,而另一个因素将加载到名义变量上)。
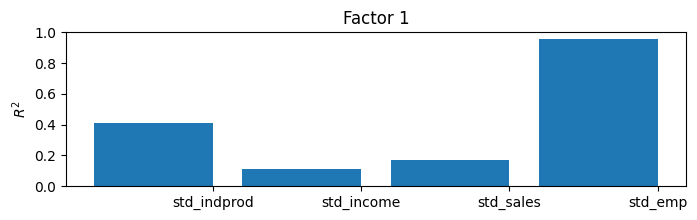
在这个模型中,只有四个内生变量和一个因子,很容易理解一个简单的 \(R^2\) 值表,但在更大的模型中就不容易了。因此,通常会使用条形图;从图中我们可以很容易地看到,该因子解释了工业生产指数的大部分变异,以及销售和就业变异的大部分,但在解释收入方面帮助不大。
[11]:
res.plot_coefficients_of_determination(figsize=(8,2));
同步指数¶
如上所述,该模型的目标是创建一个可解释的序列,可用于理解宏观经济的当前状况。这就是同步指数的设计目的。它在下面构建。对于那些对构建解释感兴趣的读者,请参阅 Kim 和 Nelson (1999) 或 Stock 和 Watson (1991)。
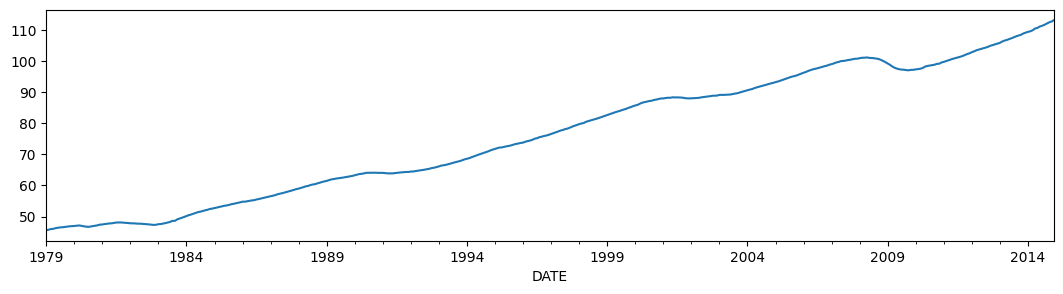
本质上,所做的是重建(差分)因子的均值。我们将把它与费城联邦储备银行发布的同步指数进行比较(FRED 上的 USPHCI)。
[12]:
usphci = DataReader('USPHCI', 'fred', start='1979-01-01', end='2014-12-01')['USPHCI']
usphci.plot(figsize=(13,3));
[13]:
dusphci = usphci.diff()[1:].values
def compute_coincident_index(mod, res):
# Estimate W(1)
spec = res.specification
design = mod.ssm['design']
transition = mod.ssm['transition']
ss_kalman_gain = res.filter_results.kalman_gain[:,:,-1]
k_states = ss_kalman_gain.shape[0]
W1 = np.linalg.inv(np.eye(k_states) - np.dot(
np.eye(k_states) - np.dot(ss_kalman_gain, design),
transition
)).dot(ss_kalman_gain)[0]
# Compute the factor mean vector
factor_mean = np.dot(W1, dta.loc['1972-02-01':, 'dln_indprod':'dln_emp'].mean())
# Normalize the factors
factor = res.factors.filtered[0]
factor *= np.std(usphci.diff()[1:]) / np.std(factor)
# Compute the coincident index
coincident_index = np.zeros(mod.nobs+1)
# The initial value is arbitrary; here it is set to
# facilitate comparison
coincident_index[0] = usphci.iloc[0] * factor_mean / dusphci.mean()
for t in range(0, mod.nobs):
coincident_index[t+1] = coincident_index[t] + factor[t] + factor_mean
# Attach dates
coincident_index = pd.Series(coincident_index, index=dta.index).iloc[1:]
# Normalize to use the same base year as USPHCI
coincident_index *= (usphci.loc['1992-07-01'] / coincident_index.loc['1992-07-01'])
return coincident_index
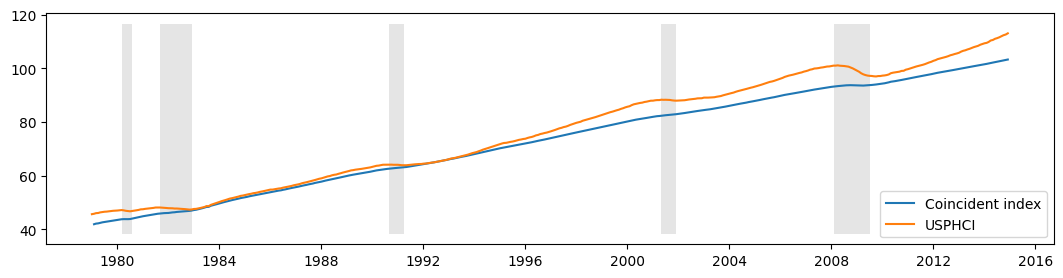
下面我们绘制了计算出的同步指数以及美国经济衰退和比较同步指数 USPHCI。
[14]:
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
coincident_index = compute_coincident_index(mod, res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, label='Coincident index')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
附录 1:扩展动态因子模型¶
回想一下,之前的规范由以下描述
以状态空间形式写出,模型的先前规范具有以下观测方程
和转移方程
the DynamicFactor 模型处理状态空间表示的设置,并在 DynamicFactor.update 方法中,它将拟合的参数值填充到相应的位置。
扩展的规范与之前的示例相同,只是我们还希望允许就业依赖于因子的滞后值。这会对 \(y_{\text{emp},t}\) 方程产生变化。现在我们有
现在,相应的观测方程应如下所示
注意,我们引入了两个新的状态变量,\(f_{t-2}\) 和 \(f_{t-3}\),这意味着我们需要更新转移方程
该模型不能由 DynamicFactor 类直接处理,但可以通过创建子类来处理,子类以适当的方式更改状态空间表示。
首先,请注意,如果我们设置了 factor_order = 4,我们几乎就得到了我们想要的东西。在这种情况下,观测方程的最后一行将是
转移方程的第一行将是
相对于我们想要的,我们有以下差异
在上述情况下,\(\lambda_{\text{emp}, j}\) 被迫为零,对于 \(j > 0\),而我们希望将它们作为参数估计。
我们只希望因子根据 AR(2) 进行转换,但在上述情况下,它是 AR(4)。
我们的策略将是子类化 DynamicFactor,并让它完成大部分工作(设置状态空间表示等),假设 factor_order = 4。我们将在子类中实际做的唯一事情是解决这两个问题。
首先,以下是子类的完整代码;下面将对其进行讨论。在开始时需要注意的是,以下定义的任何方法都不能省略。事实上,方法 __init__、start_params、param_names、transform_params、untransform_params 和 update 构成了 statsmodels 中所有状态空间模型的核心,而不仅仅是 DynamicFactor 类。
[15]:
from statsmodels.tsa.statespace import tools
class ExtendedDFM(sm.tsa.DynamicFactor):
def __init__(self, endog, **kwargs):
# Setup the model as if we had a factor order of 4
super(ExtendedDFM, self).__init__(
endog, k_factors=1, factor_order=4, error_order=2,
**kwargs)
# Note: `self.parameters` is an ordered dict with the
# keys corresponding to parameter types, and the values
# the number of parameters of that type.
# Add the new parameters
self.parameters['new_loadings'] = 3
# Cache a slice for the location of the 4 factor AR
# parameters (a_1, ..., a_4) in the full parameter vector
offset = (self.parameters['factor_loadings'] +
self.parameters['exog'] +
self.parameters['error_cov'])
self._params_factor_ar = np.s_[offset:offset+2]
self._params_factor_zero = np.s_[offset+2:offset+4]
@property
def start_params(self):
# Add three new loading parameters to the end of the parameter
# vector, initialized to zeros (for simplicity; they could
# be initialized any way you like)
return np.r_[super(ExtendedDFM, self).start_params, 0, 0, 0]
@property
def param_names(self):
# Add the corresponding names for the new loading parameters
# (the name can be anything you like)
return super(ExtendedDFM, self).param_names + [
'loading.L%d.f1.%s' % (i, self.endog_names[3]) for i in range(1,4)]
def transform_params(self, unconstrained):
# Perform the typical DFM transformation (w/o the new parameters)
constrained = super(ExtendedDFM, self).transform_params(
unconstrained[:-3])
# Redo the factor AR constraint, since we only want an AR(2),
# and the previous constraint was for an AR(4)
ar_params = unconstrained[self._params_factor_ar]
constrained[self._params_factor_ar] = (
tools.constrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[constrained, unconstrained[-3:]]
def untransform_params(self, constrained):
# Perform the typical DFM untransformation (w/o the new parameters)
unconstrained = super(ExtendedDFM, self).untransform_params(
constrained[:-3])
# Redo the factor AR unconstrained, since we only want an AR(2),
# and the previous unconstrained was for an AR(4)
ar_params = constrained[self._params_factor_ar]
unconstrained[self._params_factor_ar] = (
tools.unconstrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[unconstrained, constrained[-3:]]
def update(self, params, transformed=True, **kwargs):
# Peform the transformation, if required
if not transformed:
params = self.transform_params(params)
params[self._params_factor_zero] = 0
# Now perform the usual DFM update, but exclude our new parameters
super(ExtendedDFM, self).update(params[:-3], transformed=True, **kwargs)
# Finally, set our new parameters in the design matrix
self.ssm['design', 3, 1:4] = params[-3:]
那么我们究竟做了什么?
``__init__``
这里重要的步骤是指定我们正在使用的基本动态因子模型。具体而言,如上所述,我们使用 factor_order=4 初始化,即使我们最终将得到因子的 AR(2) 模型。我们还执行了一些与一般设置相关的任务。
``start_params``
start_params 用作优化器中的初始值。由于我们添加了三个新参数,因此我们需要将它们传递进去。如果我们没有这样做,优化器将使用默认的起始值,这些值将缺少三个元素。
``param_names``
param_names 用于多个地方,但尤其是在结果类中。下面我们获得了完整的 result 摘要,这只有在所有参数都有关联名称时才有可能。
``transform_params`` 和 ``untransform_params``
优化器以无约束的方式选择可能的参数值。这通常不是我们想要的(例如,方差不能为负),并且 transform_params 用于将优化器使用的无约束值转换为适合模型的约束值。方差项通常被平方(以强制它们为正),而 AR 滞后系数通常被约束为导致平稳模型。 untransform_params 用于反向操作(并且很重要,因为起始参数通常以适合模型的值来指定,并且我们需要将它们转换为适合优化器的参数,然后才能开始优化例程)。
即使我们不需要转换或反转换新参数(理论上载荷可以取任何值),我们仍然需要修改此函数,原因有两个。
DynamicFactor类中的版本期望的参数比我们现在少 3 个。至少,我们需要处理这三个新参数。DynamicFactor类中的版本将因子滞后系数约束为平稳的,就好像它是 AR(4) 模型一样。由于我们实际上有 AR(2) 模型,我们需要重新进行约束。我们还将最后两个自回归系数设置为零。
``update``
我们需要指定一个新的 update 方法的最重要原因是我们有三个需要放入状态空间公式中的新参数。特别是,我们让父 DynamicFactor.update 类处理将所有参数(除了三个新的参数之外)放入状态空间表示中,然后我们手动添加最后三个参数。
[16]:
# Create the model
extended_mod = ExtendedDFM(endog)
initial_extended_res = extended_mod.fit(maxiter=1000, disp=False)
extended_res = extended_mod.fit(initial_extended_res.params, method='nm', maxiter=1000)
print(extended_res.summary(separate_params=False))
Optimization terminated successfully.
Current function value: 4.686378
Iterations: 279
Function evaluations: 479
Statespace Model Results
=================================================================================================================
Dep. Variable: ['std_indprod', 'std_income', 'std_sales', 'std_emp'] No. Observations: 431
Model: DynamicFactor(factors=1, order=4) Log Likelihood -2019.829
+ AR(2) errors AIC 4085.658
Date: Thu, 03 Oct 2024 BIC 4179.178
Time: 16:08:10 HQIC 4122.583
Sample: 02-01-1979
- 12-01-2014
Covariance Type: opg
====================================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------------------------
loading.f1.std_indprod -0.7064 0.036 -19.661 0.000 -0.777 -0.636
loading.f1.std_income -0.2505 0.039 -6.460 0.000 -0.327 -0.175
loading.f1.std_sales -0.4504 0.023 -19.252 0.000 -0.496 -0.405
loading.f1.std_emp -0.4117 0.038 -10.805 0.000 -0.486 -0.337
sigma2.std_indprod 0.2338 0.045 5.156 0.000 0.145 0.323
sigma2.std_income 0.8735 0.030 29.571 0.000 0.816 0.931
sigma2.std_sales 0.5226 0.035 15.117 0.000 0.455 0.590
sigma2.std_emp 0.2599 0.023 11.352 0.000 0.215 0.305
L1.f1.f1 0.2845 0.054 5.300 0.000 0.179 0.390
L2.f1.f1 0.3890 0.058 6.686 0.000 0.275 0.503
L3.f1.f1 0 3.92e-10 0 1.000 -7.68e-10 7.68e-10
L4.f1.f1 0 3.92e-10 0 1.000 -7.68e-10 7.68e-10
L1.e(std_indprod).e(std_indprod) -0.2225 0.119 -1.864 0.062 -0.456 0.011
L2.e(std_indprod).e(std_indprod) -0.1977 0.094 -2.098 0.036 -0.382 -0.013
L1.e(std_income).e(std_income) -0.2009 0.023 -8.915 0.000 -0.245 -0.157
L2.e(std_income).e(std_income) -0.0981 0.047 -2.099 0.036 -0.190 -0.006
L1.e(std_sales).e(std_sales) -0.4842 0.047 -10.269 0.000 -0.577 -0.392
L2.e(std_sales).e(std_sales) -0.2280 0.050 -4.543 0.000 -0.326 -0.130
L1.e(std_emp).e(std_emp) 0.2325 0.041 5.707 0.000 0.153 0.312
L2.e(std_emp).e(std_emp) 0.4893 0.049 10.044 0.000 0.394 0.585
loading.L1.f1.std_emp -0.0824 0.037 -2.257 0.024 -0.154 -0.011
loading.L2.f1.std_emp -0.0065 0.035 -0.185 0.854 -0.076 0.063
loading.L3.f1.std_emp -0.1730 0.028 -6.094 0.000 -0.229 -0.117
=====================================================================================================
Ljung-Box (L1) (Q): 0.13, 0.01, 1.06, 4.34 Jarque-Bera (JB): 272.57, 10233.58, 25.49, 3815.68
Prob(Q): 0.72, 0.92, 0.30, 0.04 Prob(JB): 0.00, 0.00, 0.00, 0.00
Heteroskedasticity (H): 0.75, 4.84, 0.44, 0.44 Skew: 0.26, -0.98, 0.26, 0.78
Prob(H) (two-sided): 0.08, 0.00, 0.00, 0.00 Kurtosis: 6.86, 26.79, 4.07, 17.49
=====================================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 7.43e+17. Standard errors may be unstable.
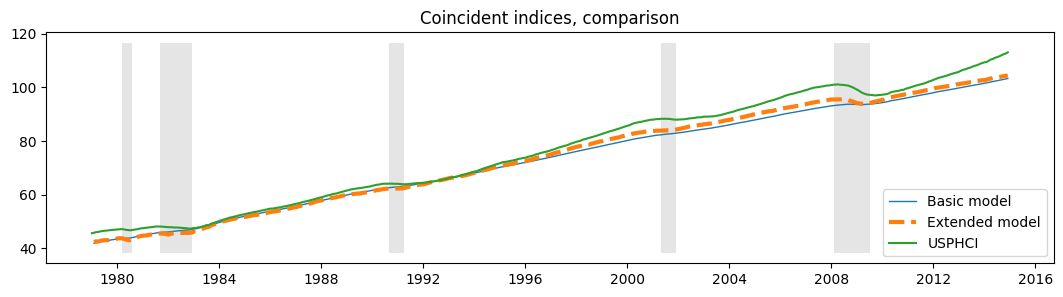
虽然此模型提高了似然性,但 AIC 和 BIC 度量并不喜欢它,因为它们会对这三个额外的参数进行惩罚。
此外,定性结果没有改变,我们可以从更新的 \(R^2\) 图表和新的同步指数中看到这一点,它们与之前的结果几乎相同。
[17]:
extended_res.plot_coefficients_of_determination(figsize=(8,2));
[18]:
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
extended_coincident_index = compute_coincident_index(extended_mod, extended_res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, '-', linewidth=1, label='Basic model')
ax.plot(dates, extended_coincident_index, '--', linewidth=3, label='Extended model')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
ax.set(title='Coincident indices, comparison')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);