预测、更新数据集和“新闻”¶
在本笔记本中,我们将描述如何使用 Statsmodels 计算更新或修订后的数据集对样本外预测或样本内缺失数据估计的影响。我们遵循“现在预测”文献的方法(见文末参考文献),使用状态空间模型来计算传入数据的“新闻”和影响。
注意:本笔记本适用于 Statsmodels v0.12+。此外,它只适用于状态空间模型或相关类,即:sm.tsa.statespace.ExponentialSmoothing、sm.tsa.arima.ARIMA、sm.tsa.SARIMAX、sm.tsa.UnobservedComponents、sm.tsa.VARMAX 和 sm.tsa.DynamicFactor。
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
macrodata = sm.datasets.macrodata.load_pandas().data
macrodata.index = pd.period_range('1959Q1', '2009Q3', freq='Q')
预测练习通常从一组固定的历史数据开始,这些数据用于模型选择和参数估计。然后,可以使用拟合的选定模型(或模型)来创建样本外预测。大多数情况下,这还不是故事的结尾。随着新数据的到来,您可能需要评估您的预测误差,可能需要更新您的模型并创建更新的样本外预测。这有时被称为“实时”预测练习(相比之下,伪实时练习是指模拟此过程的练习)。
如果所有重要的事情都是根据预测误差(如 MSE)最小化某些损失函数,那么当有新数据进来时,您可能只想使用更新的数据点完全重新进行模型选择、参数估计和样本外预测。如果这样做,您的新预测将因为两个原因而发生变化
您收到了提供新信息的新数据
您的预测模型或估计的参数不同
在本笔记本中,我们专注于隔离第一个效应的方法。我们实现此方法的方式来自所谓的“现在预测”文献,尤其是 Bańbura、Giannone 和 Reichlin (2011)、Bańbura 和 Modugno (2014) 以及 Bańbura 等人 (2014)。他们将此练习描述为计算“新闻”,我们将在 Statsmodels 中遵循他们的说法。
这些方法可能在多元模型中最有用,因为多个变量可能会同时更新,并且无法立即清楚地知道哪些更新的变量会造成哪些预测变化。但是,它们仍然可以用来思考单变量模型中的预测修正。因此,我们将从更简单的单变量情况开始解释事物的工作原理,然后转到多变量情况。
关于修正的说明:我们正在使用的框架旨在分解从新观察到的数据点中获得的预测变化。它还可以考虑先前发布的数据点的修正,但不会单独分解它们。相反,它只显示“修正”的总体影响。
关于 ``exog`` 数据的说明:我们正在使用的框架只分解从建模变量的新观察数据点中获得的预测变化。这些是 Statsmodels 中在 endog 参数中给出的“左侧”变量。此框架不会分解或考虑对未建模的“右侧”变量的变化,例如包含在 exog 参数中的变量。
简单的单变量示例:AR(1)¶
我们将从一个简单的自回归模型开始,即 AR(1)
参数 \(\phi\) 捕获了序列的持久性
我们将使用此模型来预测通货膨胀。
为了使本笔记本中预测更新的描述更简单,我们将使用已去均值化的通货膨胀数据,但在实践中,用均值项来扩充模型是直接的。
[2]:
# De-mean the inflation series
y = macrodata['infl'] - macrodata['infl'].mean()
步骤 1:在可用数据集上拟合模型¶
在这里,我们将模拟一个样本外练习,通过构建和拟合我们的模型来使用除最后五个观察值之外的所有数据。我们将假设我们还没有观察到这些值,然后在后续步骤中,我们将它们重新添加到分析中。
[3]:
y_pre = y.iloc[:-5]
y_pre.plot(figsize=(15, 3), title='Inflation');
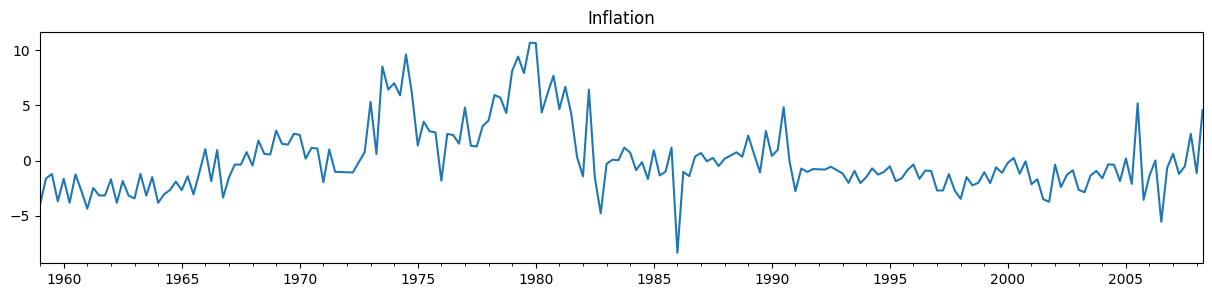
要构建预测,我们首先估计模型的参数。这将返回一个结果对象,我们可以使用它来生成预测。
[4]:
mod_pre = sm.tsa.arima.ARIMA(y_pre, order=(1, 0, 0), trend='n')
res_pre = mod_pre.fit()
print(res_pre.summary())
SARIMAX Results
==============================================================================
Dep. Variable: infl No. Observations: 198
Model: ARIMA(1, 0, 0) Log Likelihood -446.407
Date: Thu, 03 Oct 2024 AIC 896.813
Time: 15:47:15 BIC 903.390
Sample: 03-31-1959 HQIC 899.475
- 06-30-2008
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.6751 0.043 15.858 0.000 0.592 0.759
sigma2 5.3027 0.367 14.459 0.000 4.584 6.022
===================================================================================
Ljung-Box (L1) (Q): 15.65 Jarque-Bera (JB): 43.04
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 0.85 Skew: 0.18
Prob(H) (two-sided): 0.50 Kurtosis: 5.26
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
从结果对象 res 创建预测很容易 - 您只需调用 forecast 方法,并指定要构建的预测数量即可。在本例中,我们将构建四个样本外预测。
[5]:
# Compute the forecasts
forecasts_pre = res_pre.forecast(4)
# Plot the last 3 years of data and the four out-of-sample forecasts
y_pre.iloc[-12:].plot(figsize=(15, 3), label='Data', legend=True)
forecasts_pre.plot(label='Forecast', legend=True);
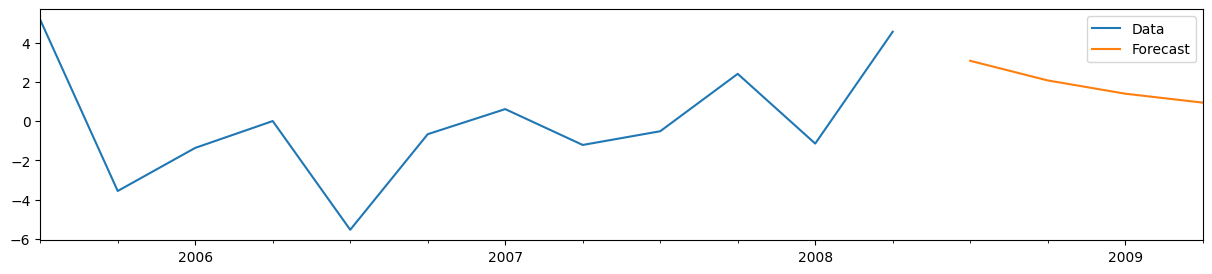
对于 AR(1) 模型,手动构建预测也很容易。将最后一个观察变量表示为 \(y_T\),将 \(h\) 步超前预测表示为 \(y_{T+h|T}\),我们有
其中 \(\hat \phi\) 是我们估计的 AR(1) 系数值。从上面的摘要输出中,我们可以看到这是模型的第一个参数,我们可以从结果对象的 params 属性中访问它。
[6]:
# Get the estimated AR(1) coefficient
phi_hat = res_pre.params[0]
# Get the last observed value of the variable
y_T = y_pre.iloc[-1]
# Directly compute the forecasts at the horizons h=1,2,3,4
manual_forecasts = pd.Series([phi_hat * y_T, phi_hat**2 * y_T,
phi_hat**3 * y_T, phi_hat**4 * y_T],
index=forecasts_pre.index)
# We'll print the two to double-check that they're the same
print(pd.concat([forecasts_pre, manual_forecasts], axis=1))
predicted_mean 0
2008Q3 3.084388 3.084388
2008Q4 2.082323 2.082323
2009Q1 1.405812 1.405812
2009Q2 0.949088 0.949088
/tmp/ipykernel_4399/554023716.py:2: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
phi_hat = res_pre.params[0]
步骤 2:从新观察结果计算“新闻”¶
假设时间已经过去,我们现在已经收到了另一个观察结果。我们的数据集现在更大,我们可以评估我们的预测误差并生成后续季度的更新预测。
[7]:
# Get the next observation after the "pre" dataset
y_update = y.iloc[-5:-4]
# Print the forecast error
print('Forecast error: %.2f' % (y_update.iloc[0] - forecasts_pre.iloc[0]))
Forecast error: -10.21
要计算基于更新数据集的预测,我们将使用 append 方法创建一个更新的结果对象 res_post,将我们的新观察结果追加到先前的 数据集。
请注意,默认情况下,append 方法不会重新估计模型的参数。这正是我们想要的,因为我们想要隔离仅新信息对预测的影响。
[8]:
# Create a new results object by passing the new observations to the `append` method
res_post = res_pre.append(y_update)
# Since we now know the value for 2008Q3, we will only use `res_post` to
# produce forecasts for 2008Q4 through 2009Q2
forecasts_post = pd.concat([y_update, res_post.forecast('2009Q2')])
print(forecasts_post)
2008Q3 -7.121330
2008Q4 -4.807732
2009Q1 -3.245783
2009Q2 -2.191284
Freq: Q-DEC, dtype: float64
在本例中,预测误差相当大 - 通货膨胀比 AR(1) 模型的预测低了 10 个百分点以上。(这主要是由于全球金融危机期间油价的大幅波动)。
为了更深入地分析这一点,我们可以使用 Statsmodels 来隔离新信息 - 或“新闻” - 对我们预测的影响。这意味着我们还不希望更改我们的模型或重新估计参数。相反,我们将使用状态空间模型结果对象中可用的 news 方法。
在 Statsmodels 中计算新闻始终需要一个先前的结果对象或数据集,以及一个更新的结果对象或数据集。在这里,我们将使用原始结果对象 res_pre 作为先前结果,并使用我们刚刚创建的 res_post 结果对象作为更新结果。
一旦我们有了先前和更新的结果对象或数据集,我们就可以通过调用 news 方法来计算新闻。在这里,我们将调用 res_pre.news,第一个参数将是更新的结果,res_post(但是,如果您有两个结果对象,则可以在这两个对象上调用 news 方法)。
除了将比较对象或数据集指定为第一个参数外,还接受各种其他参数。最重要的参数指定您要考虑的“影响期间”。这些“影响期间”对应于感兴趣的预测期间;即这些日期指定预测修正将被分解的期间。
要指定影响期间,您必须传递两个 start、end 和 periods(类似于 Pandas date_range 方法)。如果您的时间序列是一个与日期或期间索引相关联的 Pandas 对象,那么您可以将日期作为 start 和 end 的值传递,就像我们在下面所做的那样。
[9]:
# Compute the impact of the news on the four periods that we previously
# forecasted: 2008Q3 through 2009Q2
news = res_pre.news(res_post, start='2008Q3', end='2009Q2')
# Note: one alternative way to specify these impact dates is
# `start='2008Q3', periods=4`
变量 news 是 NewsResults 类的对象,它包含有关 res_post 中数据更新相对于 res_pre 的详细信息,更新数据集中的新信息以及新信息对 start 和 end 之间期间预测的影响。
一种简单的总结结果的方法是使用 summary 方法。
[10]:
print(news.summary())
News
===============================================================================
Model: ARIMA Original sample: 1959Q1
Date: Thu, 03 Oct 2024 - 2008Q2
Time: 15:47:16 Update through: 2008Q3
# of revisions: 0
# of new datapoints: 1
Impacts for [impacted variable = infl]
=========================================================
impact date estimate (prev) impact of news estimate (new)
---------------------------------------------------------
2008Q3 3.08 -10.21 -7.12
2008Q4 2.08 -6.89 -4.81
2009Q1 1.41 -4.65 -3.25
2009Q2 0.95 -3.14 -2.19
News from updated observations:
===================================================================
update date updated variable observed forecast (prev) news
-------------------------------------------------------------------
2008Q3 infl -7.12 3.08 -10.21
===================================================================
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -7.12
Name: observed, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 3.08
Name: forecast (prev), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -10.21
Name: news, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
摘要输出:此新闻结果对象的默认摘要打印了四个表格
模型和数据集的摘要
更新数据中的新闻详情
新信息对
start='2008Q3'和end='2009Q2'之间预测的影响摘要更新的数据如何导致
start='2008Q3'和end='2009Q2'之间预测的影响的详细信息
这些将在下面更详细地描述。
注意:
可以向
summary方法传递许多参数来控制此输出。有关详细信息,请查看文档/docstring。如果模型是多元的,存在多个更新,或者选择了大量的冲击日期,则显示更新和影响详细信息的表 (4) 会变得非常大。它仅在默认情况下对单变量模型显示。
第一个表格:模型和数据集的摘要
上面的第一个表格显示了
用于生成预测的模型类型。这里是一个 ARIMA 模型,因为 AR(1) 是 ARIMA(p,d,q) 模型的特例。
计算分析的日期和时间。
原始样本期间,这里对应于
y_pre更新样本期间的结束点,这里对应于
y_post中的最后一个日期
第二个表格:更新数据中的新闻
此表格只显示了先前结果中对更新样本中更新的观测值的预测。
注意:
我们的更新数据集
y_post不包含对先前观察到的数据点的任何修订。如果有,将有一个额外的表格显示每个此类修订的先前值和更新值。
第三个表格:新信息的冲击摘要
列:
上面的第三个表格显示了
每个冲击日期的先前预测,位于“估计(先前)”列中
新信息(“新闻”)对每个冲击日期预测的影响,位于“新闻影响”列中
每个冲击日期的更新预测,位于“估计(新)”列中
注意:
在多元模型中,此表包含额外的列,描述与每行相关的受影响变量。
我们的更新数据集
y_post不包含对先前观察到的数据点的任何修订。如果有,此表中将有额外的列,显示这些修订对冲击日期预测的影响。请注意,
estimate (new) = estimate (prev) + impact of news可以使用
summary_impacts方法独立访问此表。
在我们的示例中:
请注意,在我们的示例中,该表显示了我们之前计算的值
“估计(先前)”列与我们先前模型的预测相同,包含在
forecasts_pre变量中。“估计(新)”列与我们的
forecasts_post变量相同,其中包含 2008Q3 的观察值以及更新模型对 2008Q4-2009Q2 的预测。
第四个表格:更新和影响的详细信息
上面的第四个表格显示了每个新的观察结果如何转换为每个冲击日期的特定影响。
列:
前三列表格描述了相关的更新(“更新”是新的观察结果)
第一列(“更新日期”)显示更新的变量的日期。
第二列(“预测(先前)”)显示基于先前结果/数据集在更新日期对更新变量的预测值。
第三列(“观察”)显示更新结果/数据集中该更新变量/更新日期的实际观察值。
最后四列描述了给定更新的影响(影响是在“影响期间”内改变的预测)。
第四列(“冲击日期”)给出给定更新产生影响的日期。
第五列(“新闻”)显示与给定更新相关的“新闻”(这对于给定更新的每个影响都是相同的,但默认情况下不会进行稀疏化)
第六列(“权重”)描述给定更新的“新闻”在冲击日期对受影响变量的权重。通常,权重在每个“更新变量”/“更新日期”/“受影响变量”/“冲击日期”组合之间会有所不同。
第七列(“冲击”)显示给定更新对给定“受影响变量”/“冲击日期”的影响。
注意:
在多元模型中,此表包含额外的列,显示与每行相关的更新变量和受影响变量。这里,只有一个变量(“infl”),因此这些列被抑制以节省空间。
默认情况下,此表中的更新使用空格进行“稀疏化”,以避免在表格的每一行中重复相同的“更新日期”、“预测(先前)”和“观察”值。可以使用
sparsify参数覆盖此行为。请注意,
impact = news * weight。可以使用
summary_details方法独立访问此表。
在我们的示例中:
对于 2008Q3 的更新和 2008Q3 的冲击日期,权重等于 1。这是因为我们只有一个变量,并且在整合了 2008Q3 的数据后,关于该日期“预测”的剩余歧义就消失了。因此,关于该变量在 2008Q3 的所有“新闻”都直接传递到“预测”中。
附录:手动计算新闻、权重和影响¶
对于这个具有单变量模型的简单示例,可以直接手动计算上面显示的所有值。首先,回顾一下预测 \(y_{T+h|T} = \phi^h y_T\) 的公式,并注意由此我们可以得到 \(y_{T+h|T+1} = \phi^h y_{T+1}\)。最后,请注意 \(y_{T|T+1} = y_T\),因为如果我们知道通过 \(T+1\) 的观测值,我们就知道 \(y_T\) 的值。
新闻:“新闻”只不过是与新观察结果之一相关的预测误差。因此,与观察结果 \(T+1\) 相关的新闻是
冲击:新闻的影响是更新预测和先前预测之间的差值,\(i_h \equiv y_{T+h|T+1} - y_{T+h|T}\).
对于 \(h=1, \dots, 4\) 的先前预测是:\(\begin{pmatrix} \phi y_T & \phi^2 y_T & \phi^3 y_T & \phi^4 y_T \end{pmatrix}'\).
对于 \(h=1, \dots, 4\) 的更新预测是:\(\begin{pmatrix} y_{T+1} & \phi y_{T+1} & \phi^2 y_{T+1} & \phi^3 y_{T+1} \end{pmatrix}'\).
因此,冲击是
权重:要计算权重,我们只需要注意到我们可以立即用预测误差 \(n_{T+1}\) 来重写冲击。
然后权重就是 \(w = \begin{pmatrix} 1 \\ \phi \\ \phi^2 \\ \phi^3 \end{pmatrix}\)
我们可以检查一下这是否是 news 方法计算的结果。
[11]:
# Print the news, computed by the `news` method
print(news.news)
# Manually compute the news
print()
print((y_update.iloc[0] - phi_hat * y_pre.iloc[-1]).round(6))
update date updated variable
2008Q3 infl -10.205718
Name: news, dtype: float64
-10.205718
[12]:
# Print the total impacts, computed by the `news` method
# (Note: news.total_impacts = news.revision_impacts + news.update_impacts, but
# here there are no data revisions, so total and update impacts are the same)
print(news.total_impacts)
# Manually compute the impacts
print()
print(forecasts_post - forecasts_pre)
impacted variable infl
impact date
2008Q3 -10.205718
2008Q4 -6.890055
2009Q1 -4.651595
2009Q2 -3.140371
2008Q3 -10.205718
2008Q4 -6.890055
2009Q1 -4.651595
2009Q2 -3.140371
Freq: Q-DEC, dtype: float64
[13]:
# Print the weights, computed by the `news` method
print(news.weights)
# Manually compute the weights
print()
print(np.array([1, phi_hat, phi_hat**2, phi_hat**3]).round(6))
impact date 2008Q3 2008Q4 2009Q1 2009Q2
impacted variable infl infl infl infl
update date updated variable
2008Q3 infl 1.0 0.675117 0.455783 0.307707
[1. 0.675117 0.455783 0.307707]
多元示例:动态因子¶
在这个示例中,我们将考虑使用动态因子模型,根据个人消费支出(PCE)价格指数和消费者价格指数(CPI)来预测核心月度通货膨胀率。这两个指标都跟踪美国经济中的价格,并基于类似的源数据,但它们在定义上存在一些差异。尽管如此,它们在跟踪方面还是相对一致的,因此使用单个动态因子共同建模似乎是合理的。
这种方法之所以有用,其中一个原因是 CPI 比 PCE 早发布。因此,在 CPI 发布后,我们可以用这些额外的资料点来更新我们的动态因子模型,并获得对当月 PCE 发布的更精确预测。Knotek 和 Zaman (2017) 提供了这种分析的更复杂版本。
我们首先从 FRED 下载核心 CPI 和 PCE 价格指数数据,将其转换为年度化月度通货膨胀率,去除两个异常值,并对每个序列进行去均值处理(动态因子模型不会
[14]:
import pandas_datareader as pdr
levels = pdr.get_data_fred(['PCEPILFE', 'CPILFESL'], start='1999', end='2019').to_period('M')
infl = np.log(levels).diff().iloc[1:] * 1200
infl.columns = ['PCE', 'CPI']
# Remove two outliers and de-mean the series
infl.loc['2001-09':'2001-10', 'PCE'] = np.nan
为了展示其工作原理,我们将假设现在是 2017 年 4 月 14 日,这是 2017 年 3 月 CPI 发布的日期。为了展示多个更新同时生效的效果,我们将假设自 1 月底以来我们尚未更新数据,因此
我们的先前数据集将包括截至 2017 年 1 月的 PCE 和 CPI 的所有值
我们的更新数据集将额外包含 2017 年 2 月和 3 月的 CPI 以及 2017 年 2 月的 PCE 数据。但它不会包含 PCE(2017 年 3 月的 PCE 价格指数直到 2017 年 5 月 1 日才发布)。
[15]:
# Previous dataset runs through 2017-02
y_pre = infl.loc[:'2017-01'].copy()
const_pre = np.ones(len(y_pre))
print(y_pre.tail())
PCE CPI
DATE
2016-09 1.591601 2.022262
2016-10 1.540990 1.445830
2016-11 0.533425 1.631694
2016-12 1.393060 2.109728
2017-01 3.203951 2.623570
[16]:
# For the updated dataset, we'll just add in the
# CPI value for 2017-03
y_post = infl.loc[:'2017-03'].copy()
y_post.loc['2017-03', 'PCE'] = np.nan
const_post = np.ones(len(y_post))
# Notice the missing value for PCE in 2017-03
print(y_post.tail())
PCE CPI
DATE
2016-11 0.533425 1.631694
2016-12 1.393060 2.109728
2017-01 3.203951 2.623570
2017-02 2.123190 2.541355
2017-03 NaN -0.258197
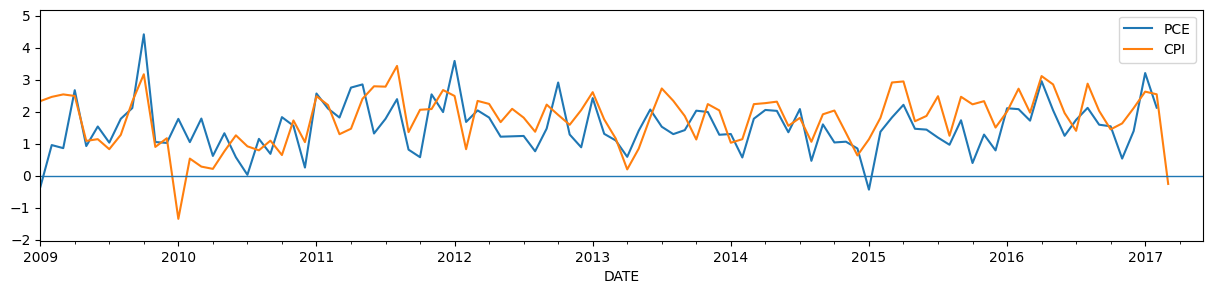
我们选择这个具体的例子,因为2017年3月,核心CPI价格自2010年以来首次下降,这些信息可能有助于预测当月的核心PCE价格。下图显示了截至4月14日观察到的CPI和PCE价格数据\(^\dagger\)。
\(\dagger\) 此说法并不完全正确,因为CPI和PCE价格指数都可以在事后进行一定程度的修正。因此,我们提取的系列并不完全等同于2017年4月14日观察到的系列。可以通过从ALFRED而不是FRED提取存档数据来解决这个问题,但我们现有的数据足以用于本教程。
[17]:
# Plot the updated dataset
fig, ax = plt.subplots(figsize=(15, 3))
y_post.plot(ax=ax)
ax.hlines(0, '2009', '2017-06', linewidth=1.0)
ax.set_xlim('2009', '2017-06');
为了进行练习,我们首先构建并拟合一个DynamicFactor模型。具体而言
我们使用单个动态因子(
k_factors=1)我们使用AR(6)模型(
factor_order=6)对因子的动态进行建模我们包含了一个以1为元素的向量作为外生变量(
exog=const_pre),因为我们正在处理的通货膨胀系列不是均值为零的。
[18]:
mod_pre = sm.tsa.DynamicFactor(y_pre, exog=const_pre, k_factors=1, factor_order=6)
res_pre = mod_pre.fit()
print(res_pre.summary())
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 12 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.81947D+00 |proj g|= 3.24664D-01
At iterate 5 f= 4.62090D+00 |proj g|= 3.53739D-01
At iterate 10 f= 2.79040D+00 |proj g|= 3.87962D-01
At iterate 15 f= 2.54688D+00 |proj g|= 1.35633D-01
At iterate 20 f= 2.45463D+00 |proj g|= 1.04853D-01
At iterate 25 f= 2.42572D+00 |proj g|= 4.92521D-02
At iterate 30 f= 2.42118D+00 |proj g|= 2.82902D-02
At iterate 35 f= 2.42077D+00 |proj g|= 6.08268D-03
At iterate 40 f= 2.42076D+00 |proj g|= 1.04046D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
12 43 66 1 0 0 3.456D-05 2.421D+00
F = 2.4207581817590249
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
Statespace Model Results
=============================================================================================
Dep. Variable: ['PCE', 'CPI'] No. Observations: 216
Model: DynamicFactor(factors=1, order=6) Log Likelihood -522.884
+ 1 regressors AIC 1069.768
Date: Thu, 03 Oct 2024 BIC 1110.271
Time: 15:48:15 HQIC 1086.131
Sample: 02-28-1999
- 01-31-2017
Covariance Type: opg
===================================================================================
Ljung-Box (L1) (Q): 4.50, 0.54 Jarque-Bera (JB): 13.09, 12.63
Prob(Q): 0.03, 0.46 Prob(JB): 0.00, 0.00
Heteroskedasticity (H): 0.56, 0.44 Skew: 0.18, -0.16
Prob(H) (two-sided): 0.02, 0.00 Kurtosis: 4.15, 4.14
Results for equation PCE
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
loading.f1 0.5499 0.061 9.037 0.000 0.431 0.669
beta.const 1.7039 0.095 17.959 0.000 1.518 1.890
Results for equation CPI
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
loading.f1 0.9033 0.102 8.875 0.000 0.704 1.103
beta.const 1.9621 0.137 14.357 0.000 1.694 2.230
Results for factor equation f1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
L1.f1 0.1246 0.069 1.805 0.071 -0.011 0.260
L2.f1 0.1823 0.072 2.548 0.011 0.042 0.323
L3.f1 0.0178 0.073 0.244 0.807 -0.125 0.160
L4.f1 -0.0700 0.078 -0.893 0.372 -0.224 0.084
L5.f1 0.1561 0.068 2.308 0.021 0.024 0.289
L6.f1 0.1376 0.075 1.842 0.066 -0.009 0.284
Error covariance matrix
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2.PCE 0.5422 0.065 8.287 0.000 0.414 0.670
sigma2.CPI 1.322e-12 0.144 9.15e-12 1.000 -0.283 0.283
==============================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
有了拟合好的模型,我们现在可以构建与观察2017年3月CPI相关的新闻和影响。更新后的数据是2017年2月和2017年3月部分的数据,我们将考察其对3月和4月的影响。
在单变量示例中,我们首先创建了一个更新后的结果对象,然后将其传递给news方法。在这里,我们通过直接传递更新后的数据集来创建新闻。
注意
y_post包含整个更新后的数据集(不仅仅是新的数据点)我们还需要传递一个更新后的
exog数组。该数组必须涵盖**两者**与
y_post相关的整个时间段y_post结束后的任何额外数据点,一直到由end指定的最后一个影响日期
在这里,
y_post在2017年3月结束,因此我们需要将我们的exog扩展到2017年4月,多一个时间段。
[19]:
# Create the news results
# Note
const_post_plus1 = np.ones(len(y_post) + 1)
news = res_pre.news(y_post, exog=const_post_plus1, start='2017-03', end='2017-04')
注意:
在上面的单变量示例中,我们首先构建了一个新的结果对象,然后将其传递给
news方法。我们也可以在这里这样做,不过需要一个额外的步骤。由于我们正在请求超过y_post结束时间段的影响,因此我们仍然需要在该时间段内将exog变量的额外值传递给newsres_post = res_pre.apply(y_post, exog=const_post) news = res_pre.news(res_post, exog=[1.], start='2017-03', end='2017-04')
现在我们已经计算了news,打印summary是查看结果的一种便捷方式。
[20]:
# Show the summary of the news results
print(news.summary())
News
===============================================================================
Model: DynamicFactor Original sample: 1999-02
Date: Thu, 03 Oct 2024 - 2017-01
Time: 15:48:16 Update through: 2017-03
# of revisions: 0
# of new datapoints: 3
Impacts
===========================================================================
impact date impacted variable estimate (prev) impact of news estimate (new)
---------------------------------------------------------------------------
2017-03 CPI 2.07 -2.33 -0.26
NaT PCE 1.77 -1.42 0.35
2017-04 CPI 1.90 -0.23 1.67
NaT PCE 1.67 -0.14 1.53
News from updated observations:
===================================================================
update date updated variable observed forecast (prev) news
-------------------------------------------------------------------
2017-02 CPI 2.54 2.24 0.30
PCE 2.12 1.87 0.25
2017-03 CPI -0.26 2.07 -2.33
===================================================================
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 2.07
1 1.77
2 1.90
3 1.67
Name: estimate (prev), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 0.00
1 0.00
2 0.00
3 0.00
Name: impact of revisions, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -2.33
1 -1.42
2 -0.23
3 -0.14
Name: impact of news, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -2.33
1 -1.42
2 -0.23
3 -0.14
Name: total impact, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -0.26
1 0.35
2 1.67
3 1.53
Name: estimate (new), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 2.54
1 2.12
2 -0.26
Name: observed, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 2.24
1 1.87
2 2.07
Name: forecast (prev), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 0.30
1 0.25
2 -2.33
Name: news, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
由于我们有多个变量,默认情况下,摘要只显示更新数据沿线的新闻和总影响。
从第一个表中我们可以看到,我们的更新数据集包含三个新的数据点,其中大部分“新闻”来自2017年3月非常低的读数。
第二个表显示,这三个数据点对2017年3月PCE的估计值(尚未观察到)产生了重大影响。该估计值下调了近1.5个百分点。
更新后的数据也影响了第一个样本外月份(2017年4月)的预测。在整合了新的数据之后,该模型对该月份CPI和PCE通货膨胀的预测分别下调了0.29个百分点和0.17个百分点。
虽然这些表格显示了“新闻”和总影响,但它们没有显示每个影响有多少是由每个更新的数据点造成的。为了查看这些信息,我们需要查看详细表格。
查看详细表格的一种方法是将include_details=True传递给summary方法。但是,为了避免重复上面的表格,我们将直接调用summary_details方法。
[21]:
print(news.summary_details())
Details of news for [updated variable = CPI]
======================================================================================================
update date observed forecast (prev) impact date impacted variable news weight impact
------------------------------------------------------------------------------------------------------
2017-02 2.54 2.24 2017-04 CPI 0.30 0.18 0.06
PCE 0.30 0.11 0.03
2017-03 -0.26 2.07 2017-03 CPI -2.33 1.0 -2.33
PCE -2.33 0.61 -1.42
2017-04 CPI -2.33 0.12 -0.29
PCE -2.33 0.08 -0.18
======================================================================================================
该表显示,上面描述的对2017年4月PCE估计值的大部分修正,来自2017年3月CPI发布相关的新闻。相反,2月CPI发布对4月预测的影响很小,而2月PCE发布基本上没有影响。
参考文献¶
Bańbura, Marta, Domenico Giannone, and Lucrezia Reichlin. “Nowcasting.” The Oxford Handbook of Economic Forecasting. July 8, 2011.
Bańbura, Marta, Domenico Giannone, Michele Modugno, and Lucrezia Reichlin. “Now-casting and the real-time data flow.” In Handbook of economic forecasting, vol. 2, pp. 195-237. Elsevier, 2013.
Bańbura, Marta, and Michele Modugno. “Maximum likelihood estimation of factor models on datasets with arbitrary pattern of missing data.” Journal of Applied Econometrics 29, no. 1 (2014): 133-160.
Knotek, Edward S., and Saeed Zaman. “Nowcasting US headline and core inflation.” Journal of Money, Credit and Banking 49, no. 5 (2017): 931-968.