时间序列数据中的季节性¶
考虑用多个不同周期性的季节性成分对时间序列数据进行建模的问题。让我们以时间序列 \(y_t\) 为例，并将其明确分解为一个水平成分和两个季节性成分。
\[y_t = \mu_t + \gamma^{(1)}_t + \gamma^{(2)}_t\]
其中 \(\mu_t\) 代表趋势或水平，\(\gamma^{(1)}_t\) 代表周期相对较短的季节性成分，\(\gamma^{(2)}_t\) 代表周期较长的另一个季节性成分。我们的水平将有一个固定的截距项，并考虑 \(\gamma^{(2)}_t\) 和 \(\gamma^{(2)}_t\) 都是随机的，以便季节性模式可以随时间变化。
在本笔记本中，我们将生成符合此模型的合成数据，并在未观察到的成分建模框架下展示对季节性项的建模方式。
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.rc("figure", figsize=(16,8))
plt.rc("font", size=14)
合成数据创建¶
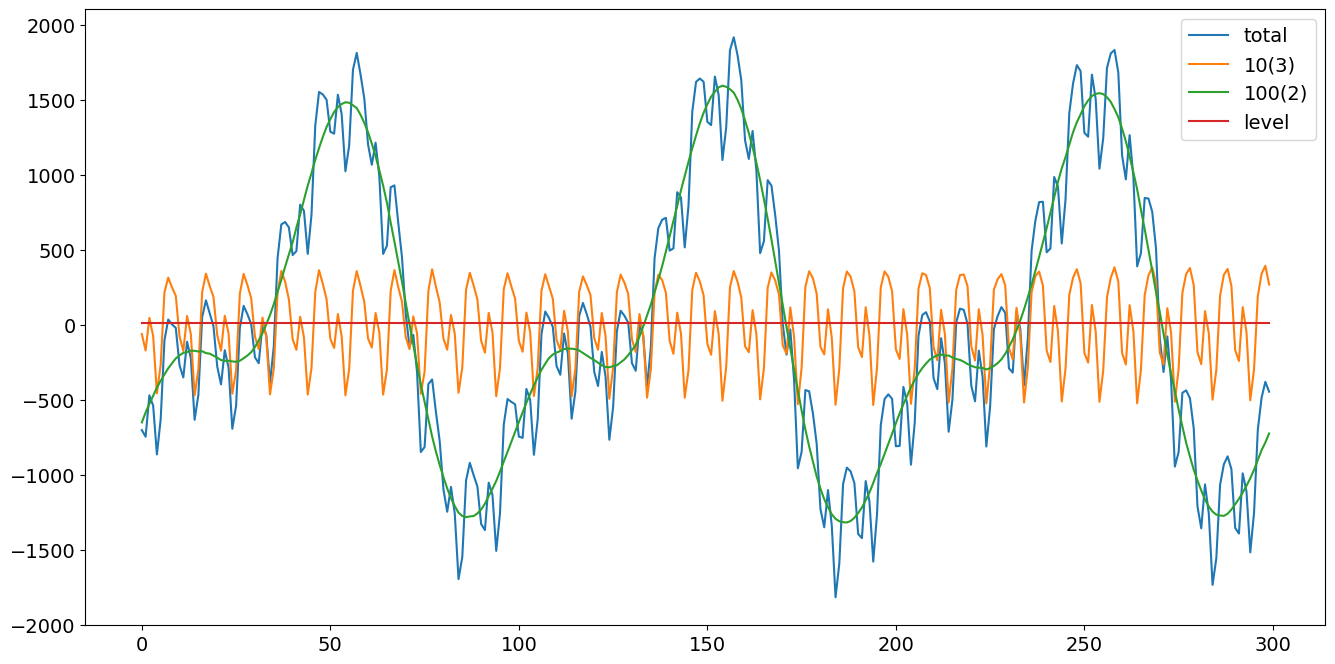
我们将按照 Durbin 和 Koopman (2012) 中的公式 (3.7) 和 (3.8) 创建具有多个季节性模式的数据。我们将模拟 300 个时期和两个在频域中参数化的季节性项，它们的周期分别为 10 和 100，谐波数分别为 3 和 2。此外，它们随机部分的方差分别为 4 和 9。
[3]:
# First we'll simulate the synthetic data
def simulate_seasonal_term(periodicity, total_cycles, noise_std=1.,
harmonics=None):
duration = periodicity * total_cycles
assert duration == int(duration)
duration = int(duration)
harmonics = harmonics if harmonics else int(np.floor(periodicity / 2))
lambda_p = 2 * np.pi / float(periodicity)
gamma_jt = noise_std * np.random.randn((harmonics))
gamma_star_jt = noise_std * np.random.randn((harmonics))
total_timesteps = 100 * duration # Pad for burn in
series = np.zeros(total_timesteps)
for t in range(total_timesteps):
gamma_jtp1 = np.zeros_like(gamma_jt)
gamma_star_jtp1 = np.zeros_like(gamma_star_jt)
for j in range(1, harmonics + 1):
cos_j = np.cos(lambda_p * j)
sin_j = np.sin(lambda_p * j)
gamma_jtp1[j - 1] = (gamma_jt[j - 1] * cos_j
+ gamma_star_jt[j - 1] * sin_j
+ noise_std * np.random.randn())
gamma_star_jtp1[j - 1] = (- gamma_jt[j - 1] * sin_j
+ gamma_star_jt[j - 1] * cos_j
+ noise_std * np.random.randn())
series[t] = np.sum(gamma_jtp1)
gamma_jt = gamma_jtp1
gamma_star_jt = gamma_star_jtp1
wanted_series = series[-duration:] # Discard burn in
return wanted_series
[4]:
duration = 100 * 3
periodicities = [10, 100]
num_harmonics = [3, 2]
std = np.array([2, 3])
np.random.seed(8678309)
terms = []
for ix, _ in enumerate(periodicities):
s = simulate_seasonal_term(
periodicities[ix],
duration / periodicities[ix],
harmonics=num_harmonics[ix],
noise_std=std[ix])
terms.append(s)
terms.append(np.ones_like(terms[0]) * 10.)
series = pd.Series(np.sum(terms, axis=0))
df = pd.DataFrame(data={'total': series,
'10(3)': terms[0],
'100(2)': terms[1],
'level':terms[2]})
h1, = plt.plot(df['total'])
h2, = plt.plot(df['10(3)'])
h3, = plt.plot(df['100(2)'])
h4, = plt.plot(df['level'])
plt.legend(['total','10(3)','100(2)', 'level'])
plt.show()
未观察到的成分 (频域建模)¶
下一个方法是未观察到的成分模型，其中趋势被建模为一个固定的截距，季节性成分被建模为使用三角函数，它们的初级周期分别为 10 和 100，谐波数分别为 3 和 2。请注意，这是正确的生成模型。时间序列过程可以写成
\[\begin{split}\begin{align} y_t & = \mu_t + \gamma^{(1)}_t + \gamma^{(2)}_t + \epsilon_t\\ \mu_{t+1} & = \mu_t \\ \gamma^{(1)}_{t} &= \sum_{j=1}^2 \gamma^{(1)}_{j, t} \\ \gamma^{(2)}_{t} &= \sum_{j=1}^3 \gamma^{(2)}_{j, t}\\ \gamma^{(1)}_{j, t+1} &= \gamma^{(1)}_{j, t}\cos(\lambda_j) + \gamma^{*, (1)}_{j, t}\sin(\lambda_j) + \omega^{(1)}_{j,t}, ~j = 1, 2, 3\\ \gamma^{*, (1)}_{j, t+1} &= -\gamma^{(1)}_{j, t}\sin(\lambda_j) + \gamma^{*, (1)}_{j, t}\cos(\lambda_j) + \omega^{*, (1)}_{j, t}, ~j = 1, 2, 3\\ \gamma^{(2)}_{j, t+1} &= \gamma^{(2)}_{j, t}\cos(\lambda_j) + \gamma^{*, (2)}_{j, t}\sin(\lambda_j) + \omega^{(2)}_{j,t}, ~j = 1, 2\\ \gamma^{*, (2)}_{j, t+1} &= -\gamma^{(2)}_{j, t}\sin(\lambda_j) + \gamma^{*, (2)}_{j, t}\cos(\lambda_j) + \omega^{*, (2)}_{j, t}, ~j = 1, 2\\ \end{align}\end{split}\]
其中 \(\epsilon_t\) 是白噪声，\(\omega^{(1)}_{j,t}\) 是 i.i.d. \(N(0, \sigma^2_1)\)，而 \(\omega^{(2)}_{j,t}\) 是 i.i.d. \(N(0, \sigma^2_2)\)，其中 \(\sigma_1 = 2.\)
[5]:
model = sm.tsa.UnobservedComponents(series.values,
level='fixed intercept',
freq_seasonal=[{'period': 10,
'harmonics': 3},
{'period': 100,
'harmonics': 2}])
res_f = model.fit(disp=False)
print(res_f.summary())
# The first state variable holds our estimate of the intercept
print("fixed intercept estimated as {0:.3f}".format(res_f.smoother_results.smoothed_state[0,-1:][0]))
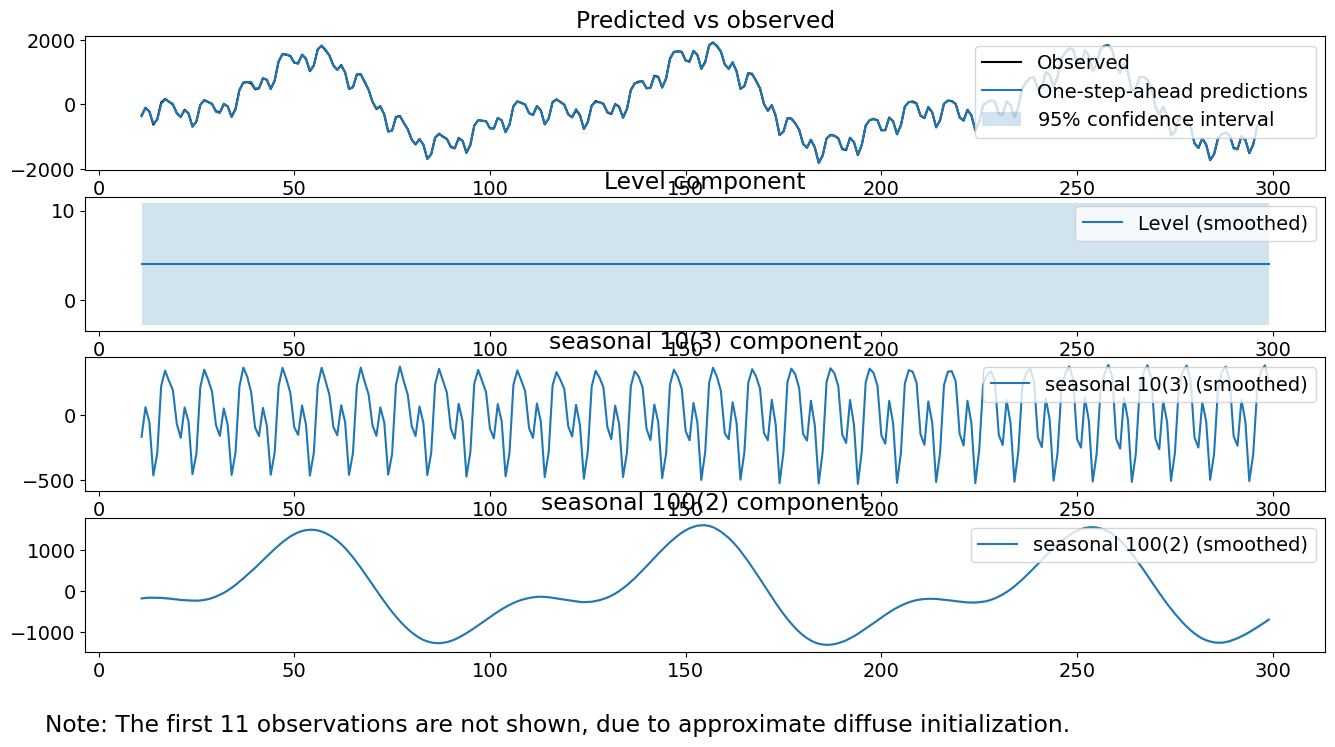
res_f.plot_components()
plt.show()
Unobserved Components Results
==============================================================================================
Dep. Variable: y No. Observations: 300
Model: fixed intercept Log Likelihood -1145.631
+ stochastic freq_seasonal(10(3)) AIC 2295.261
+ stochastic freq_seasonal(100(2)) BIC 2302.594
Date: Thu, 03 Oct 2024 HQIC 2298.200
Time: 15:59:12
Sample: 0
- 300
Covariance Type: opg
===============================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------------------
sigma2.freq_seasonal_10(3) 4.5942 0.565 8.126 0.000 3.486 5.702
sigma2.freq_seasonal_100(2) 9.7904 2.483 3.942 0.000 4.923 14.658
===================================================================================
Ljung-Box (L1) (Q): 0.06 Jarque-Bera (JB): 0.08
Prob(Q): 0.81 Prob(JB): 0.96
Heteroskedasticity (H): 1.17 Skew: 0.01
Prob(H) (two-sided): 0.45 Kurtosis: 3.08
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
fixed intercept estimated as 4.053
[6]:
model.ssm.transition[:, :, 0]
[6]:
array([[ 1. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. ],
[ 0. , 0.80901699, 0.58778525, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. ],
[ 0. , -0.58778525, 0.80901699, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. ],
[ 0. , 0. , 0. , 0.30901699, 0.95105652,
0. , 0. , 0. , 0. , 0. ,
0. ],
[ 0. , 0. , 0. , -0.95105652, 0.30901699,
0. , 0. , 0. , 0. , 0. ,
0. ],
[ 0. , 0. , 0. , 0. , 0. ,
-0.30901699, 0.95105652, 0. , 0. , 0. ,
0. ],
[ 0. , 0. , 0. , 0. , 0. ,
-0.95105652, -0.30901699, 0. , 0. , 0. ,
0. ],
[ 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.99802673, 0.06279052, 0. ,
0. ],
[ 0. , 0. , 0. , 0. , 0. ,
0. , 0. , -0.06279052, 0.99802673, 0. ,
0. ],
[ 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.9921147 ,
0.12533323],
[ 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , -0.12533323,
0.9921147 ]])
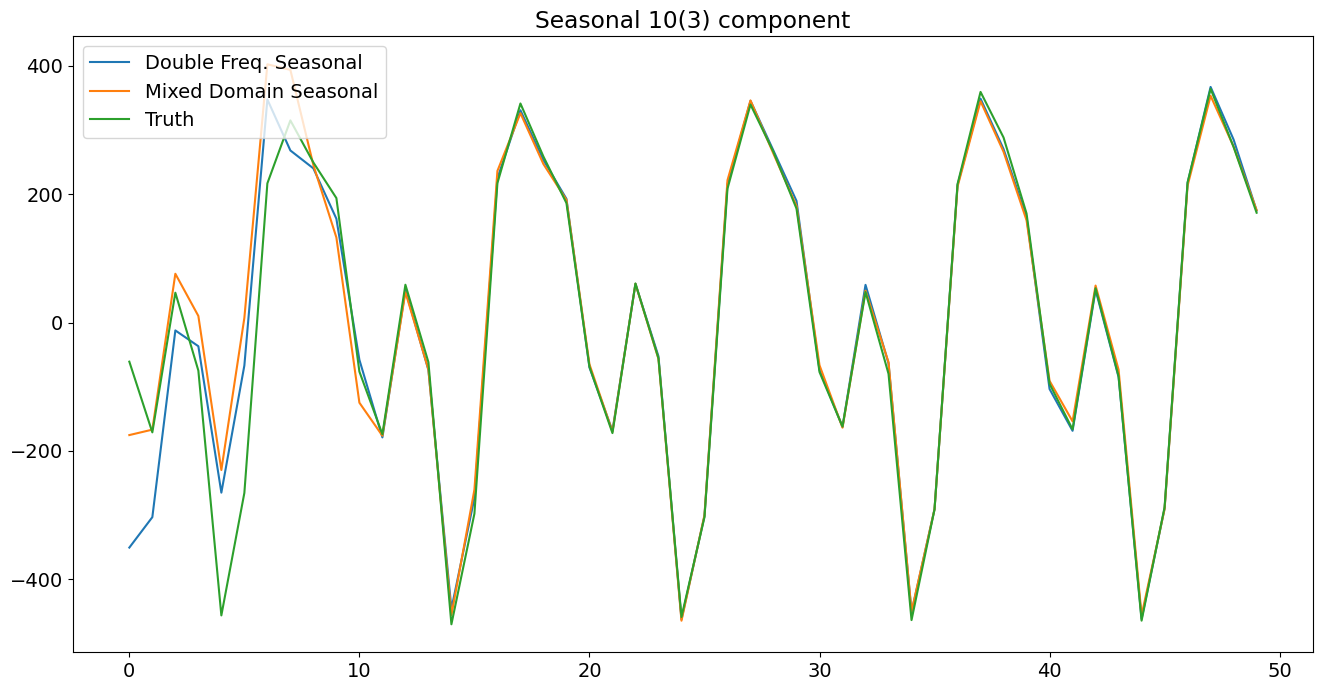
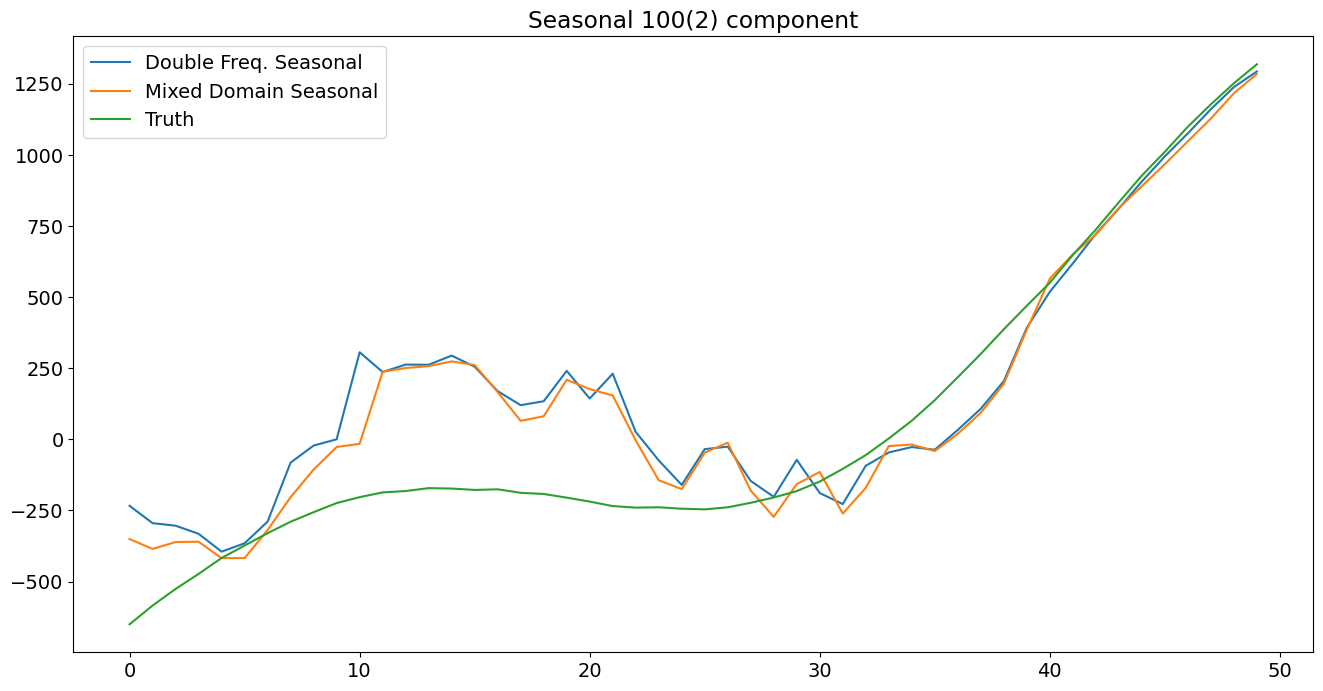
观察到拟合的方差非常接近 4 和 9 的真实方差。此外，各个季节性成分看起来非常接近真实的季节性成分。平滑的水平项有点接近 10 的真实水平。最后，我们的诊断看起来很可靠；检验统计量足够小，无法拒绝我们的三个检验。
未观察到的成分 (混合时域和频域建模)¶
第二个方法是未观察到的成分模型，其中趋势被建模为一个固定的截距，季节性成分被建模为使用 10 个常数（总和为 0）和三角函数（初级周期为 100，总谐波数为 2）。请注意，这不是生成模型，因为它假定较短的季节性成分比实际情况有更多状态误差。时间序列过程可以写成
\[\begin{split}\begin{align} y_t & = \mu_t + \gamma^{(1)}_t + \gamma^{(2)}_t + \epsilon_t\\ \mu_{t+1} & = \mu_t \\ \gamma^{(1)}_{t + 1} &= - \sum_{j=1}^9 \gamma^{(1)}_{t + 1 - j} + \omega^{(1)}_t\\ \gamma^{(2)}_{j, t+1} &= \gamma^{(2)}_{j, t}\cos(\lambda_j) + \gamma^{*, (2)}_{j, t}\sin(\lambda_j) + \omega^{(2)}_{j,t}, ~j = 1, 2\\ \gamma^{*, (2)}_{j, t+1} &= -\gamma^{(2)}_{j, t}\sin(\lambda_j) + \gamma^{*, (2)}_{j, t}\cos(\lambda_j) + \omega^{*, (2)}_{j, t}, ~j = 1, 2\\ \end{align}\end{split}\]
其中 \(\epsilon_t\) 是白噪声，\(\omega^{(1)}_{t}\) 是 i.i.d. \(N(0, \sigma^2_1)\)，而 \(\omega^{(2)}_{j,t}\) 是 i.i.d. \(N(0, \sigma^2_2)\)。
[7]:
model = sm.tsa.UnobservedComponents(series,
level='fixed intercept',
seasonal=10,
freq_seasonal=[{'period': 100,
'harmonics': 2}])
res_tf = model.fit(disp=False)
print(res_tf.summary())
# The first state variable holds our estimate of the intercept
print("fixed intercept estimated as {0:.3f}".format(res_tf.smoother_results.smoothed_state[0,-1:][0]))
fig = res_tf.plot_components()
fig.tight_layout(pad=1.0)
Unobserved Components Results
==============================================================================================
Dep. Variable: y No. Observations: 300
Model: fixed intercept Log Likelihood -1238.113
+ stochastic seasonal(10) AIC 2480.226
+ stochastic freq_seasonal(100(2)) BIC 2487.538
Date: Thu, 03 Oct 2024 HQIC 2483.157
Time: 15:59:14
Sample: 0
- 300
Covariance Type: opg
===============================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------------------
sigma2.seasonal 55.2934 7.114 7.773 0.000 41.351 69.236
sigma2.freq_seasonal_100(2) 28.6897 4.008 7.159 0.000 20.835 36.544
===================================================================================
Ljung-Box (L1) (Q): 26.35 Jarque-Bera (JB): 1.20
Prob(Q): 0.00 Prob(JB): 0.55
Heteroskedasticity (H): 1.27 Skew: -0.14
Prob(H) (two-sided): 0.24 Kurtosis: 2.87
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
fixed intercept estimated as 4.468
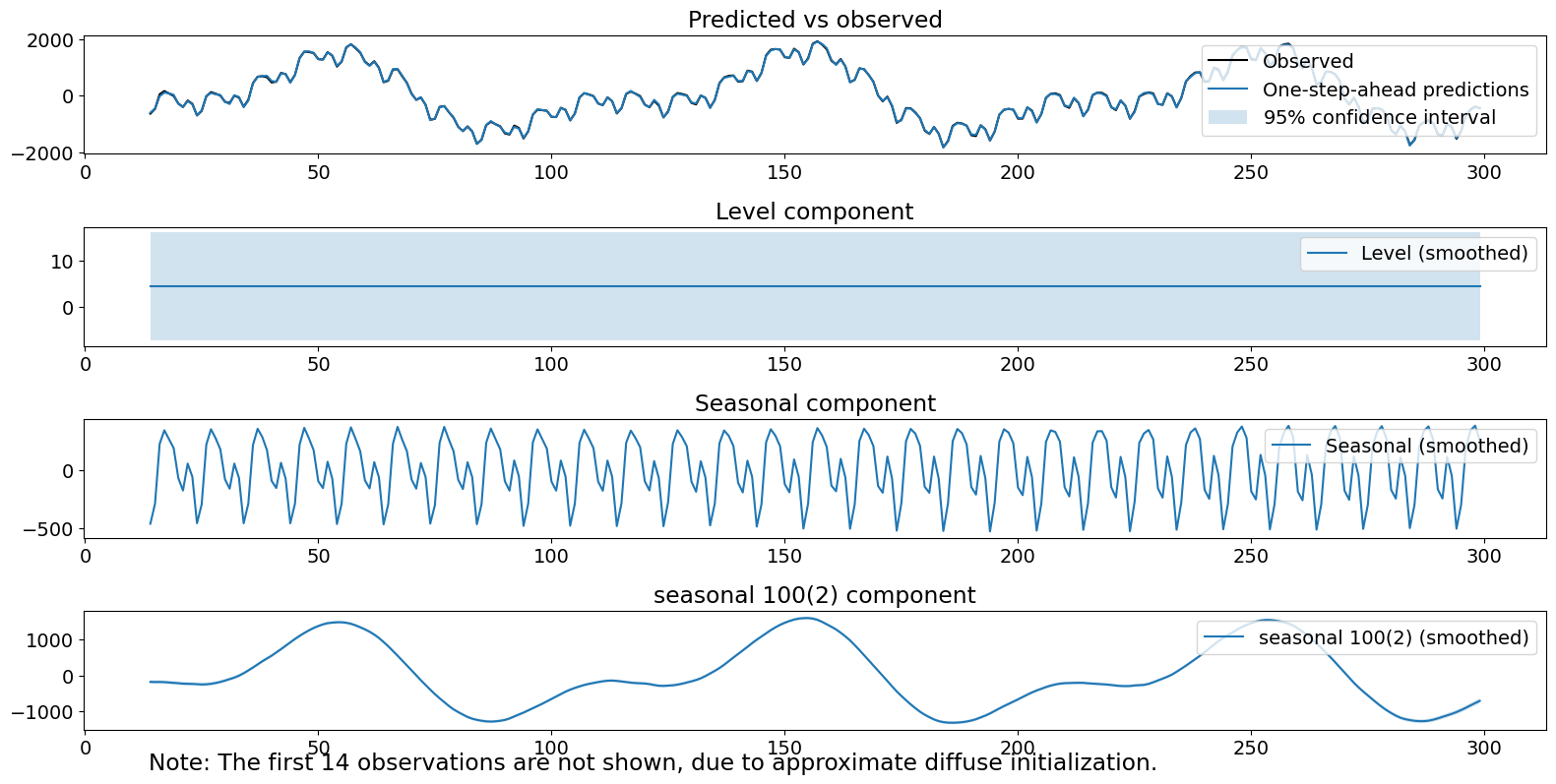
绘制的成分看起来不错。但是，第二个季节性项的估计方差被夸大了。此外，我们拒绝了 Ljung-Box 统计量，表明在考虑了我们的成分后，我们可能仍然存在自相关。
未观察到的成分 (懒惰的频域建模)¶
第三个方法是未观察到的成分模型，它具有一个固定的截距和一个季节性成分，该成分使用三角函数建模，其初级周期为 100，谐波数为 50。请注意，这不是生成模型，因为它假定比实际情况有更多谐波。由于方差是绑定的，我们无法将不存在的谐波的估计协方差降低到 0。这种模型规范的“懒惰”之处在于，我们没有费心去指定两个不同的季节性成分，而是选择使用一个具有足够谐波来覆盖这两个成分的成分来对它们进行建模。我们无法捕获两个真实成分之间方差的任何差异。时间序列过程可以写成
\[\begin{split}\begin{align} y_t & = \mu_t + \gamma^{(1)}_t + \epsilon_t\\ \mu_{t+1} &= \mu_t\\ \gamma^{(1)}_{t} &= \sum_{j=1}^{50}\gamma^{(1)}_{j, t}\\ \gamma^{(1)}_{j, t+1} &= \gamma^{(1)}_{j, t}\cos(\lambda_j) + \gamma^{*, (1)}_{j, t}\sin(\lambda_j) + \omega^{(1}_{j,t}, ~j = 1, 2, \dots, 50\\ \gamma^{*, (1)}_{j, t+1} &= -\gamma^{(1)}_{j, t}\sin(\lambda_j) + \gamma^{*, (1)}_{j, t}\cos(\lambda_j) + \omega^{*, (1)}_{j, t}, ~j = 1, 2, \dots, 50\\ \end{align}\end{split}\]
其中 \(\epsilon_t\) 是白噪声，\(\omega^{(1)}_{t}\) 是 i.i.d. \(N(0, \sigma^2_1)\)。
[8]:
model = sm.tsa.UnobservedComponents(series,
level='fixed intercept',
freq_seasonal=[{'period': 100}])
res_lf = model.fit(disp=False)
print(res_lf.summary())
# The first state variable holds our estimate of the intercept
print("fixed intercept estimated as {0:.3f}".format(res_lf.smoother_results.smoothed_state[0,-1:][0]))
fig = res_lf.plot_components()
fig.tight_layout(pad=1.0)
Unobserved Components Results
===============================================================================================
Dep. Variable: y No. Observations: 300
Model: fixed intercept Log Likelihood -1101.455
+ stochastic freq_seasonal(100(50)) AIC 2204.910
Date: Thu, 03 Oct 2024 BIC 2208.204
Time: 16:06:42 HQIC 2206.243
Sample: 0
- 300
Covariance Type: opg
================================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------------------
sigma2.freq_seasonal_100(50) 0.7591 0.082 9.233 0.000 0.598 0.920
===================================================================================
Ljung-Box (L1) (Q): 85.96 Jarque-Bera (JB): 0.72
Prob(Q): 0.00 Prob(JB): 0.70
Heteroskedasticity (H): 1.00 Skew: -0.01
Prob(H) (two-sided): 0.99 Kurtosis: 2.71
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
fixed intercept estimated as 4.426
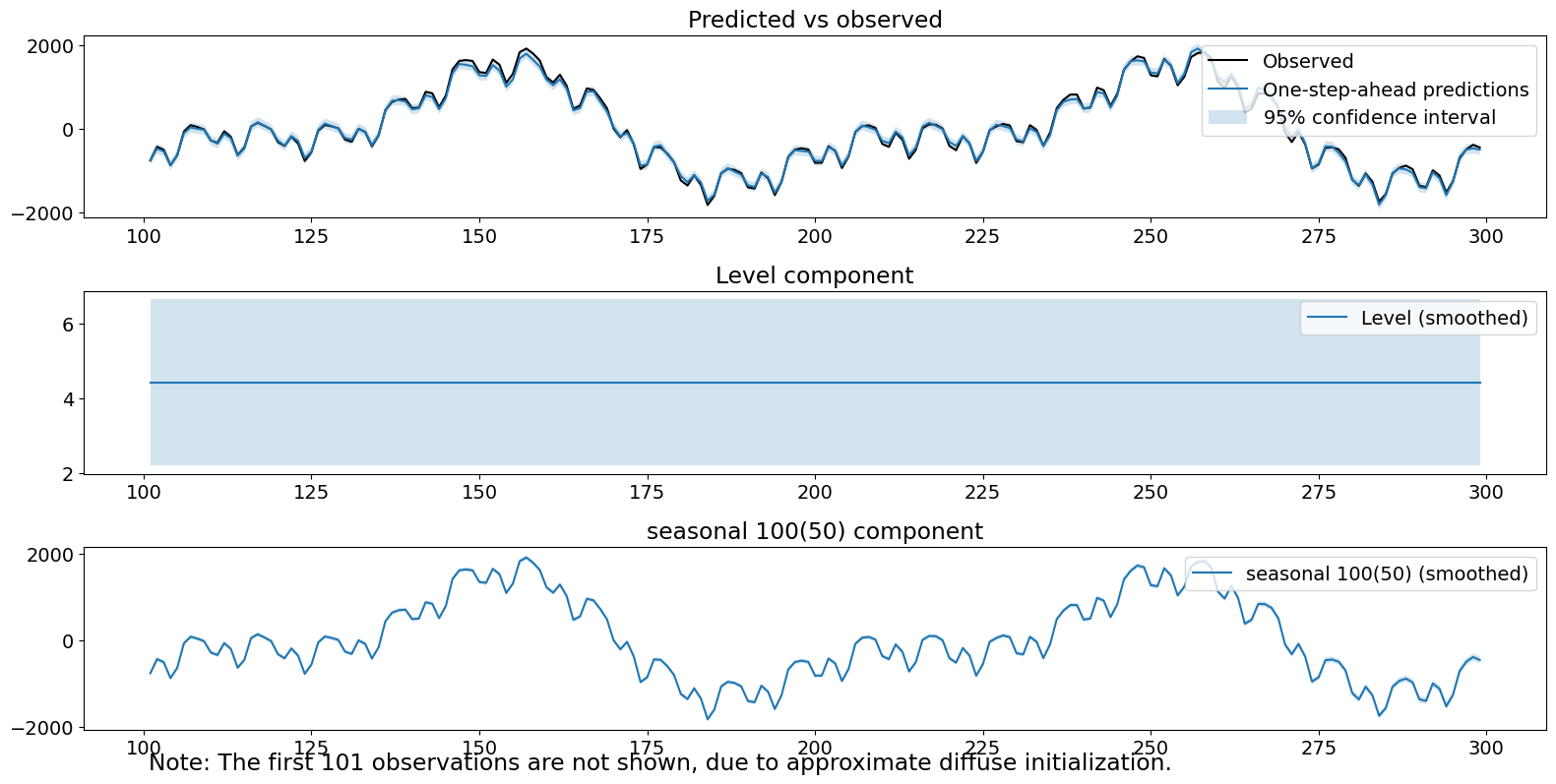
请注意，我们的一个诊断检验将在 0.05 的水平上被拒绝。
未观察到的成分 (懒惰的时域季节性建模)¶
第四个方法是未观察到的成分模型，它具有一个固定的截距和一个使用 100 个常数的时域季节性模型来建模的季节性成分。时间序列过程可以写成
\[\begin{split}\begin{align} y_t & =\mu_t + \gamma^{(1)}_t + \epsilon_t\\ \mu_{t+1} &= \mu_{t} \\ \gamma^{(1)}_{t + 1} &= - \sum_{j=1}^{99} \gamma^{(1)}_{t + 1 - j} + \omega^{(1)}_t\\ \end{align}\end{split}\]
其中 \(\epsilon_t\) 是白噪声，\(\omega^{(1)}_{t}\) 是 i.i.d. \(N(0, \sigma^2_1)\)。
[9]:
model = sm.tsa.UnobservedComponents(series,
level='fixed intercept',
seasonal=100)
res_lt = model.fit(disp=False)
print(res_lt.summary())
# The first state variable holds our estimate of the intercept
print("fixed intercept estimated as {0:.3f}".format(res_lt.smoother_results.smoothed_state[0,-1:][0]))
fig = res_lt.plot_components()
fig.tight_layout(pad=1.0)
Unobserved Components Results
======================================================================================
Dep. Variable: y No. Observations: 300
Model: fixed intercept Log Likelihood -1564.378
+ stochastic seasonal(100) AIC 3130.756
Date: Thu, 03 Oct 2024 BIC 3134.054
Time: 16:07:26 HQIC 3132.091
Sample: 0
- 300
Covariance Type: opg
===================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
sigma2.seasonal 3.558e+05 2.96e+04 12.012 0.000 2.98e+05 4.14e+05
===================================================================================
Ljung-Box (L1) (Q): 200.79 Jarque-Bera (JB): 25.29
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 0.49 Skew: 0.85
Prob(H) (two-sided): 0.00 Kurtosis: 3.37
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
fixed intercept estimated as 4.690
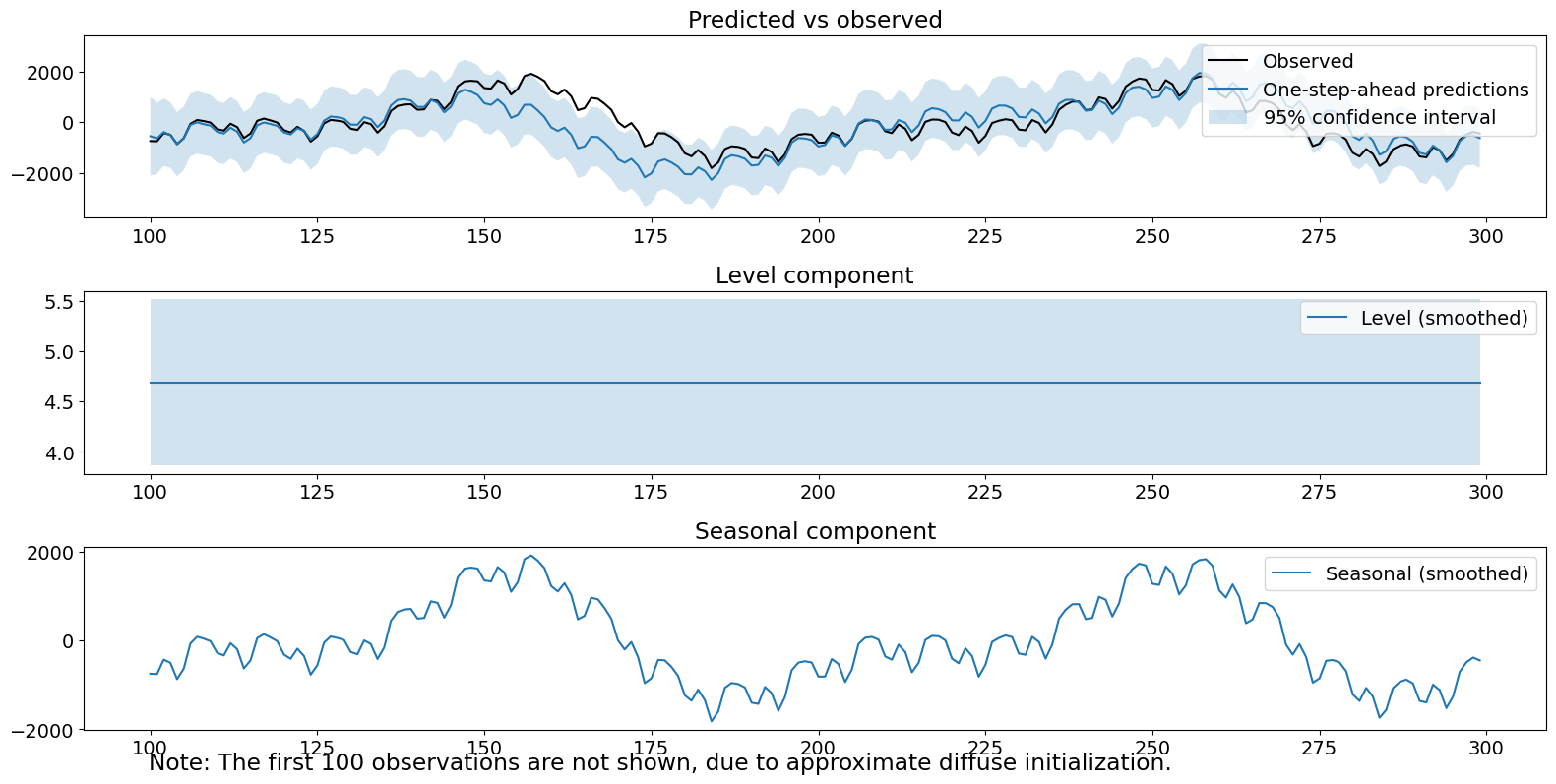
季节性成分本身看起来不错，它是主要信号。季节性项的估计方差非常高 (\(>10^5\))，导致我们在一步预测中存在很大的不确定性，并且对新数据的响应速度很慢，如一步预测和观测中的巨大误差所证明。最后，我们三个诊断检验都被拒绝了。
滤波估计的比较¶
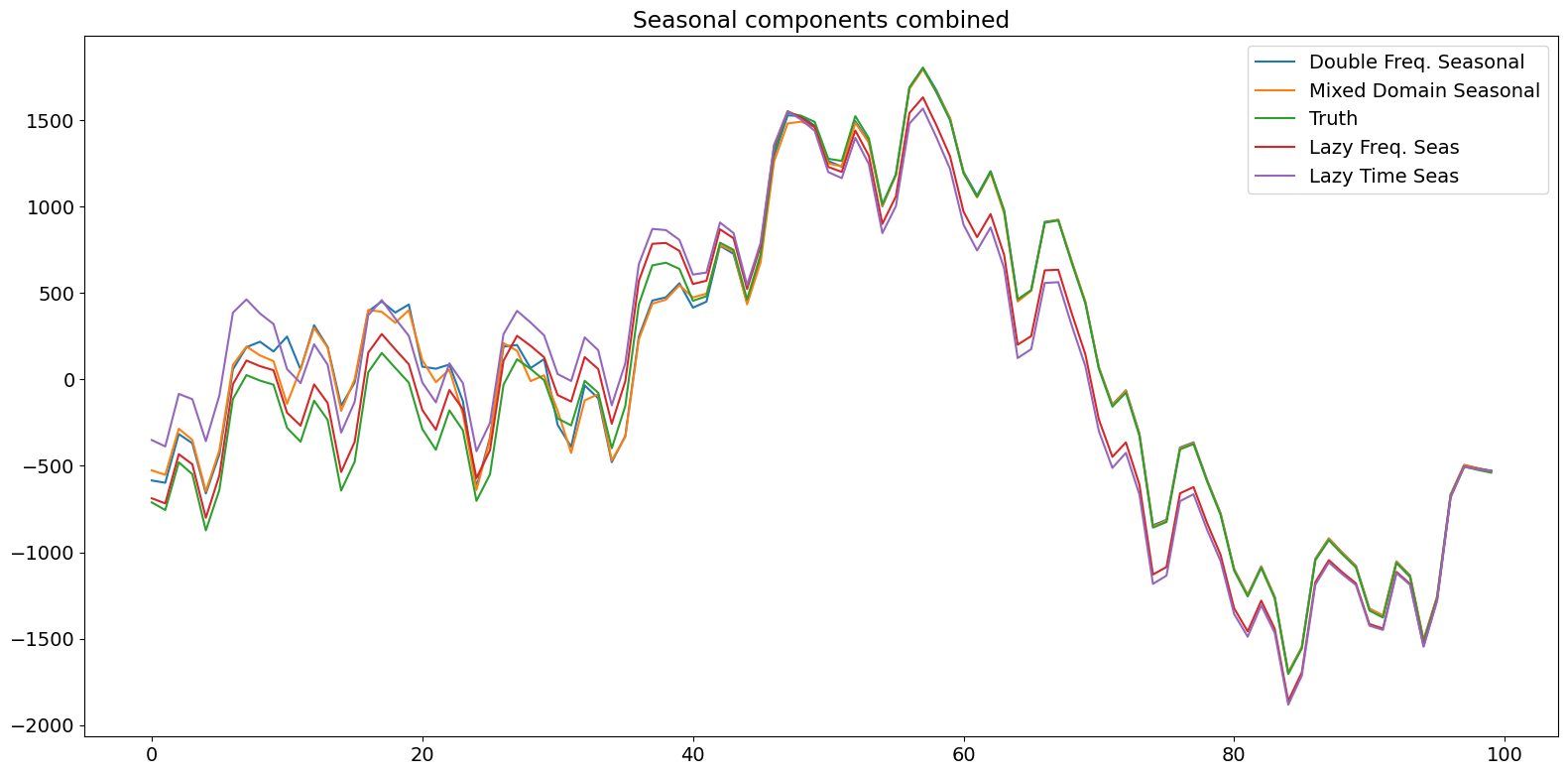
下面的图显示，显式地对各个成分进行建模会导致滤波状态在大约半个周期内接近真实状态。懒惰模型在组合的真实状态上花了更长时间（几乎是一个完整周期）来做到这一点。
[10]:
# Assign better names for our seasonal terms
true_seasonal_10_3 = terms[0]
true_seasonal_100_2 = terms[1]
true_sum = true_seasonal_10_3 + true_seasonal_100_2
[11]:
time_s = np.s_[:50] # After this they basically agree
fig1 = plt.figure()
ax1 = fig1.add_subplot(111)
idx = np.asarray(series.index)
h1, = ax1.plot(idx[time_s], res_f.freq_seasonal[0].filtered[time_s], label='Double Freq. Seas')
h2, = ax1.plot(idx[time_s], res_tf.seasonal.filtered[time_s], label='Mixed Domain Seas')
h3, = ax1.plot(idx[time_s], true_seasonal_10_3[time_s], label='True Seasonal 10(3)')
plt.legend([h1, h2, h3], ['Double Freq. Seasonal','Mixed Domain Seasonal','Truth'], loc=2)
plt.title('Seasonal 10(3) component')
plt.show()
[12]:
time_s = np.s_[:50] # After this they basically agree
fig2 = plt.figure()
ax2 = fig2.add_subplot(111)
h21, = ax2.plot(idx[time_s], res_f.freq_seasonal[1].filtered[time_s], label='Double Freq. Seas')
h22, = ax2.plot(idx[time_s], res_tf.freq_seasonal[0].filtered[time_s], label='Mixed Domain Seas')
h23, = ax2.plot(idx[time_s], true_seasonal_100_2[time_s], label='True Seasonal 100(2)')
plt.legend([h21, h22, h23], ['Double Freq. Seasonal','Mixed Domain Seasonal','Truth'], loc=2)
plt.title('Seasonal 100(2) component')
plt.show()
[13]:
time_s = np.s_[:100]
fig3 = plt.figure()
ax3 = fig3.add_subplot(111)
h31, = ax3.plot(idx[time_s], res_f.freq_seasonal[1].filtered[time_s] + res_f.freq_seasonal[0].filtered[time_s], label='Double Freq. Seas')
h32, = ax3.plot(idx[time_s], res_tf.freq_seasonal[0].filtered[time_s] + res_tf.seasonal.filtered[time_s], label='Mixed Domain Seas')
h33, = ax3.plot(idx[time_s], true_sum[time_s], label='True Seasonal 100(2)')
h34, = ax3.plot(idx[time_s], res_lf.freq_seasonal[0].filtered[time_s], label='Lazy Freq. Seas')
h35, = ax3.plot(idx[time_s], res_lt.seasonal.filtered[time_s], label='Lazy Time Seas')
plt.legend([h31, h32, h33, h34, h35], ['Double Freq. Seasonal','Mixed Domain Seasonal','Truth', 'Lazy Freq. Seas', 'Lazy Time Seas'], loc=1)
plt.title('Seasonal components combined')
plt.tight_layout(pad=1.0)
结论¶
在本笔记本中，我们模拟了一个具有两个不同周期季节性成分的时间序列。我们使用结构化时间序列模型对它们进行了建模，这些模型包括 (a) 具有正确周期和谐波数的两个频域成分，(b) 较短项的时域季节性成分和具有正确周期和谐波数的频域项，(c) 具有较长周期和完整谐波数的单个频域项，以及 (d) 具有较长周期的单个时域项。我们看到了各种诊断结果，只有正确的生成模型 (a) 未能拒绝任何检验。因此，更灵活的季节性建模（允许具有可指定谐波的多个成分）可以成为时间序列建模的有用工具。最后，我们可以用更少的总状态来表示季节性成分，从而允许用户尝试自己进行偏差方差权衡，而不是被迫选择“懒惰”模型，这些模型使用大量的状态并因此产生额外的方差。
最后更新时间：2024 年 10 月 3 日