SARIMAX:简介¶
此笔记本复制了 Stata ARIMA 时间序列估计和后估计文档中的示例。
首先,我们将复制四个估计示例 http://www.stata.com/manuals13/tsarima.pdf
美国批发价格指数 (WPI) 数据集上的 ARIMA(1,1,1) 模型。
示例 1 的变体,在 ARIMA(1,1,1) 规范中添加 MA(4) 项以允许加性季节效应。
每月航空数据的 ARIMA(2,1,0) x (1,1,0,12) 模型。此示例允许乘法季节效应。
具有外生回归量的 ARMA(1,1) 模型;描述消费作为自回归过程,其中货币供应也被认为是解释变量。
其次,我们将演示后估计功能以复制 http://www.stata.com/manuals13/tsarimapostestimation.pdf。示例 4 中的模型用于演示
一步提前样本内预测
n 步提前样本外预测
n 步提前样本内动态预测
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
from scipy.stats import norm
import statsmodels.api as sm
import matplotlib.pyplot as plt
from datetime import datetime
import requests
from io import BytesIO
# Register converters to avoid warnings
pd.plotting.register_matplotlib_converters()
plt.rc("figure", figsize=(16,8))
plt.rc("font", size=14)
ARIMA 示例 1:Arima¶
如示例 2 中的图表所示,批发价格指数 (WPI) 随时间推移而增长(即不平稳)。因此,ARMA 模型不是一个好的规范。在这个第一个示例中,我们考虑了一个模型,其中原始时间序列被假定为一阶积分的,因此差分被假定为平稳的,并拟合了一个具有一个自回归滞后和一个移动平均滞后的模型,以及一个截距项。
然后假设的数据过程是
其中 \(c\) 是 ARMA 模型的截距,\(\Delta\) 是首差算子,我们假设 \(\epsilon_{t} \sim N(0, \sigma^2)\)。这可以改写成强调滞后多项式,如下所示(这将在下面的示例 2 中很有用)
其中 \(L\) 是滞后算子。
请注意,Stata 输出和下面输出之间的一个区别是 Stata 估计了以下模型
其中 \(\beta_0\) 是过程 \(y_t\) 的均值。此模型等效于 statsmodels SARIMAX 类中估计的模型,但解释不同。要查看等效性,请注意
这样 \(c = (1 - \phi_1) \beta_0\)。
[3]:
# Dataset
wpi1 = requests.get('https://www.stata-press.com/data/r12/wpi1.dta').content
data = pd.read_stata(BytesIO(wpi1))
data.index = data.t
# Set the frequency
data.index.freq="QS-OCT"
# Fit the model
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,1))
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: wpi No. Observations: 124
Model: SARIMAX(1, 1, 1) Log Likelihood -135.351
Date: Thu, 03 Oct 2024 AIC 278.703
Time: 16:05:55 BIC 289.951
Sample: 01-01-1960 HQIC 283.272
- 10-01-1990
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0943 0.068 1.389 0.165 -0.039 0.227
ar.L1 0.8742 0.055 16.028 0.000 0.767 0.981
ma.L1 -0.4120 0.100 -4.119 0.000 -0.608 -0.216
sigma2 0.5257 0.053 9.849 0.000 0.421 0.630
===================================================================================
Ljung-Box (L1) (Q): 0.09 Jarque-Bera (JB): 9.78
Prob(Q): 0.77 Prob(JB): 0.01
Heteroskedasticity (H): 15.93 Skew: 0.28
Prob(H) (two-sided): 0.00 Kurtosis: 4.26
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
因此,最大似然估计意味着对于上面的过程,我们有
其中 \(\epsilon_{t} \sim N(0, 0.5257)\)。最后,回想一下 \(c = (1 - \phi_1) \beta_0\),这里 \(c = 0.0943\) 且 \(\phi_1 = 0.8742\)。为了与 Stata 的输出进行比较,我们可以计算均值
注意:此值与 Stata 文档中的值几乎相同,\(\beta_0 = 0.7498\)。轻微的差异可能是由于舍入以及所用数值优化器的停止准则的细微差异造成的。
ARIMA 示例 2:带有加性季节效应的 Arima¶
此模型是示例 1 中模型的扩展。这里数据被假定为遵循以下过程
此模型的新部分是允许存在年度季节效应(即使周期性为 4,它也是年度的,因为数据集是季度性的)。第二个区别是,此模型使用数据的对数而不是级别。
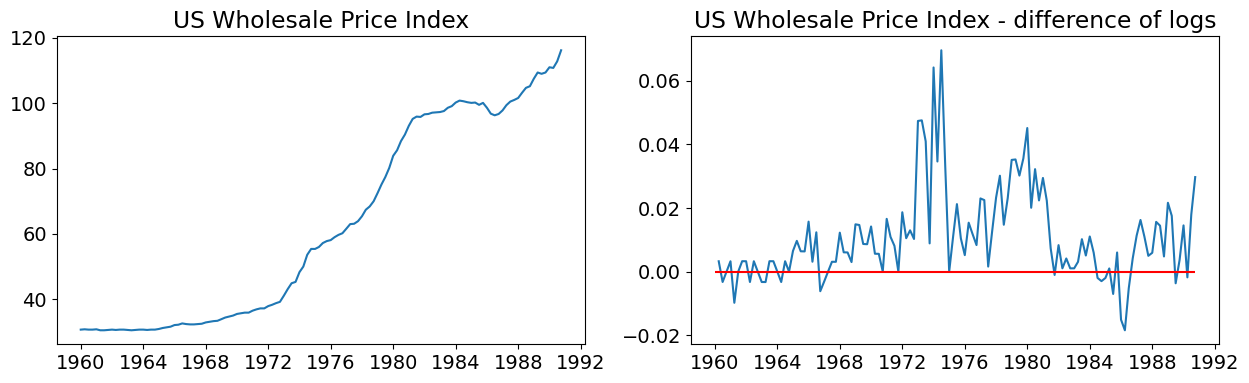
在估计数据集之前,显示以下内容的图表:
时间序列(以对数形式)
时间序列的首差(以对数形式)
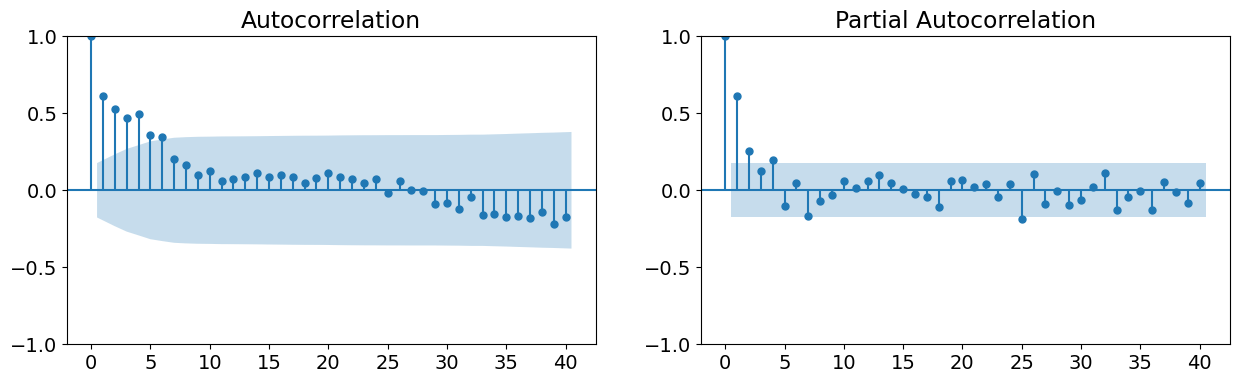
自相关函数
偏自相关函数。
从前两个图表中,我们注意到原始时间序列似乎不平稳,而首差则是平稳的。这支持在数据的首差上估计 ARMA 模型,或者估计具有 1 阶积分的 ARIMA 模型(回想一下,我们采用的是后一种方法)。最后两个图表支持使用 ARMA(1,1,1) 模型。
[4]:
# Dataset
data = pd.read_stata(BytesIO(wpi1))
data.index = data.t
data.index.freq="QS-OCT"
data['ln_wpi'] = np.log(data['wpi'])
data['D.ln_wpi'] = data['ln_wpi'].diff()
[5]:
# Graph data
fig, axes = plt.subplots(1, 2, figsize=(15,4))
# Levels
axes[0].plot(data.index._mpl_repr(), data['wpi'], '-')
axes[0].set(title='US Wholesale Price Index')
# Log difference
axes[1].plot(data.index._mpl_repr(), data['D.ln_wpi'], '-')
axes[1].hlines(0, data.index[0], data.index[-1], 'r')
axes[1].set(title='US Wholesale Price Index - difference of logs');
[6]:
# Graph data
fig, axes = plt.subplots(1, 2, figsize=(15,4))
fig = sm.graphics.tsa.plot_acf(data.iloc[1:]['D.ln_wpi'], lags=40, ax=axes[0])
fig = sm.graphics.tsa.plot_pacf(data.iloc[1:]['D.ln_wpi'], lags=40, ax=axes[1])
要了解如何在 statsmodels 中指定此模型,首先回顾一下,在示例 1 中,我们使用了以下代码来指定 ARIMA(1,1,1) 模型
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,1))
The order 参数是一个元组,形式为 (AR specification, Integration order, MA specification)。积分阶数必须是整数(例如,这里我们假设一个积分阶数,因此它被指定为 1。在底层数据已经平稳的纯 ARMA 模型中,它将是 0)。
对于 AR 规范和 MA 规范组件,有两种可能性。第一个是指定相应的滞后多项式的最大次数,在这种情况下,该组件是整数。例如,如果我们要指定 ARIMA(1,1,4) 过程,我们将使用
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,4))
并且相应的数据过程将是
或
当规范参数作为滞后多项式的最大次数给出时,这意味着包含所有直到该次数的所有多项式项。请注意,这不是我们想要使用的模型,因为它将包括 \(\epsilon_{t-2}\) 和 \(\epsilon_{t-3}\) 的项,而我们在这里不想要这些项。
我们想要的是一个多项式,该多项式具有 1 次和 4 次的项,但省略了 2 次和 3 次的项。为此,我们需要为规范参数提供一个元组,其中元组描述滞后多项式本身。特别是,这里我们想使用
ar = 1 # this is the maximum degree specification
ma = (1,0,0,1) # this is the lag polynomial specification
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(ar,1,ma)))
这给出了以下形式的数据过程
这是我们想要的。
[7]:
# Fit the model
mod = sm.tsa.statespace.SARIMAX(data['ln_wpi'], trend='c', order=(1,1,(1,0,0,1)))
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
=================================================================================
Dep. Variable: ln_wpi No. Observations: 124
Model: SARIMAX(1, 1, [1, 4]) Log Likelihood 386.034
Date: Thu, 03 Oct 2024 AIC -762.067
Time: 16:06:14 BIC -748.006
Sample: 01-01-1960 HQIC -756.355
- 10-01-1990
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0024 0.002 1.485 0.138 -0.001 0.006
ar.L1 0.7808 0.094 8.269 0.000 0.596 0.966
ma.L1 -0.3993 0.126 -3.174 0.002 -0.646 -0.153
ma.L4 0.3087 0.120 2.572 0.010 0.073 0.544
sigma2 0.0001 9.8e-06 11.114 0.000 8.97e-05 0.000
===================================================================================
Ljung-Box (L1) (Q): 0.02 Jarque-Bera (JB): 45.15
Prob(Q): 0.90 Prob(JB): 0.00
Heteroskedasticity (H): 2.58 Skew: 0.29
Prob(H) (two-sided): 0.00 Kurtosis: 5.91
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ARIMA 示例 3:航空公司模型¶
在前面的示例中,我们以加性方式包含了季节效应,这意味着我们在模型中添加了一个项,允许该过程依赖于第 4 个 MA 滞后。相反,我们可能想要以乘法方式对季节效应进行建模。我们通常将模型写成 ARIMA \((p,d,q) \times (P,D,Q)_s\),其中小写字母表示非季节分量的规范,大写字母表示季节分量的规范;\(s\) 是季节的周期性(例如,它通常是季度的 4 或月度的 12)。数据过程可以以上述通用形式编写为
其中
\(\phi_p (L)\) 是非季节性自回归滞后多项式
\(\tilde \phi_P (L^s)\) 是季节性自回归滞后多项式
\(\Delta^d \Delta_s^D y_t\) 是时间序列,差分了 \(d\) 次,并季节性地差分了 \(D\) 次。
\(A(t)\) 是趋势多项式(包括截距)
\(\theta_q (L)\) 是非季节性移动平均滞后多项式
\(\tilde \theta_Q (L^s)\) 是季节性移动平均滞后多项式
有时我们将它改写为
其中 \(y_t^* = \Delta^d \Delta_s^D y_t\)。这强调了与简单情况一样,在我们对数据进行差分(这里是非季节性和季节性)以使数据平稳之后,得到的模型只是一个 ARMA 模型。
例如,考虑航空公司模型 ARIMA \((2,1,0) \times (1,1,0)_{12}\),带有一个截距。数据过程可以以上述形式编写为
这里,我们有
\(\phi_p (L) = (1 - \phi_1 L - \phi_2 L^2)\)
\(\tilde \phi_P (L^s) = (1 - \phi_1 L^12)\)
\(d = 1, D = 1, s=12\) 表示 \(y_t^*\) 是通过对 \(y_t\) 进行首差,然后进行第 12 次差分得出的。
\(A(t) = c\) 是常数趋势多项式(即只是一个截距)
\(\theta_q (L) = \tilde \theta_Q (L^s) = 1\)(即没有移动平均效应)
看到时间序列变量前面的两个滞后多项式可能仍然令人困惑,但请注意,我们可以将滞后多项式乘在一起得到以下模型
可以改写为
这类似于示例 2 中的加性季节模型,但自回归滞后前面的系数实际上是潜在的季节性和非季节性参数的组合。
在 statsmodels 中指定模型只需添加 seasonal_order 参数,该参数接受形式为 (Seasonal AR specification, Seasonal Integration order, Seasonal MA, Seasonal periodicity) 的元组。季节性 AR 和 MA 规范与以前一样,可以表示为最大多项式次数或滞后多项式本身。季节性周期是一个整数。
对于带有截距的航空公司模型 ARIMA \((2,1,0) \times (1,1,0)_{12}\),命令是
mod = sm.tsa.statespace.SARIMAX(data['lnair'], order=(2,1,0), seasonal_order=(1,1,0,12))
[8]:
# Dataset
air2 = requests.get('https://www.stata-press.com/data/r12/air2.dta').content
data = pd.read_stata(BytesIO(air2))
data.index = pd.date_range(start=datetime(int(data.time[0]), 1, 1), periods=len(data), freq='MS')
data['lnair'] = np.log(data['air'])
# Fit the model
mod = sm.tsa.statespace.SARIMAX(data['lnair'], order=(2,1,0), seasonal_order=(1,1,0,12), simple_differencing=True)
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==========================================================================================
Dep. Variable: D.DS12.lnair No. Observations: 131
Model: SARIMAX(2, 0, 0)x(1, 0, 0, 12) Log Likelihood 240.821
Date: Thu, 03 Oct 2024 AIC -473.643
Time: 16:06:19 BIC -462.142
Sample: 02-01-1950 HQIC -468.970
- 12-01-1960
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.4057 0.080 -5.045 0.000 -0.563 -0.248
ar.L2 -0.0799 0.099 -0.809 0.419 -0.274 0.114
ar.S.L12 -0.4723 0.072 -6.592 0.000 -0.613 -0.332
sigma2 0.0014 0.000 8.403 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 0.72
Prob(Q): 0.91 Prob(JB): 0.70
Heteroskedasticity (H): 0.54 Skew: 0.14
Prob(H) (two-sided): 0.04 Kurtosis: 3.23
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
请注意,这里我们使用了额外的参数 simple_differencing=True。这控制了 ARIMA 模型中积分顺序的处理方式。如果 simple_differencing=True,则作为 endog 提供的时间序列将被实际差分,并将对生成的新的时间序列拟合 ARMA 模型。这意味着将有许多初始周期丢失到差分过程,但是可能需要将结果与其他包进行比较(例如 Stata 的 arima 始终使用简单差分)或如果季节性周期很大。
默认值为 simple_differencing=False,在这种情况下,积分组件作为状态空间公式的一部分实现,并且所有原始数据都可以在估计中使用。
ARIMA 示例 4:ARMAX (弗里德曼)¶
此模型演示了如何使用解释变量(ARMAX 的 X 部分)。当包含外生回归量时,SARIMAX 模块使用“带有 SARIMA 误差的回归”的概念(有关带有 ARIMA 误差的回归与替代规范的详细信息,请参阅 http://robjhyndman.com/hyndsight/arimax/),以便模型指定为
请注意,第一个方程只是一个线性回归,第二个方程只是描述了误差分量作为 SARIMA 的过程(如示例 3 中所述)。这种规范的一个原因是估计的参数具有其自然解释。
此规范嵌入了许多更简单的规范。例如,带有 AR(2) 误差的回归是
本示例中考虑的模型是带有 ARMA(1,1) 误差的回归。然后将该过程写为
请注意,\(\beta_0\) 如上例 1 中所述,不等同于由 trend='c' 指定的截距。虽然在上面的示例中,我们通过趋势多项式估计了模型的截距,但在这里,我们演示了如何通过将常量添加到外生数据集中来估计 \(\beta_0\) 本身。在输出中,\(beta_0\) 被称为 const,而上面截距 \(c\) 在输出中被称为 intercept。
[9]:
# Dataset
friedman2 = requests.get('https://www.stata-press.com/data/r12/friedman2.dta').content
data = pd.read_stata(BytesIO(friedman2))
data.index = data.time
data.index.freq = "QS-OCT"
# Variables
endog = data.loc['1959':'1981', 'consump']
exog = sm.add_constant(data.loc['1959':'1981', 'm2'])
# Fit the model
mod = sm.tsa.statespace.SARIMAX(endog, exog, order=(1,0,1))
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: consump No. Observations: 92
Model: SARIMAX(1, 0, 1) Log Likelihood -340.508
Date: Thu, 03 Oct 2024 AIC 691.015
Time: 16:06:21 BIC 703.624
Sample: 01-01-1959 HQIC 696.105
- 10-01-1981
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -36.0606 56.643 -0.637 0.524 -147.078 74.957
m2 1.1220 0.036 30.824 0.000 1.051 1.193
ar.L1 0.9348 0.041 22.717 0.000 0.854 1.015
ma.L1 0.3091 0.089 3.488 0.000 0.135 0.483
sigma2 93.2556 10.889 8.565 0.000 71.914 114.597
===================================================================================
Ljung-Box (L1) (Q): 0.04 Jarque-Bera (JB): 23.49
Prob(Q): 0.84 Prob(JB): 0.00
Heteroskedasticity (H): 22.51 Skew: 0.17
Prob(H) (two-sided): 0.00 Kurtosis: 5.45
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ARIMA 后估计:示例 1 - 动态预测¶
这里,我们描述了 statsmodels 的 SARIMAX 的一些后估计功能。
首先,使用示例中的模型,我们使用不包括最后几个观测值的数据来估计参数(这是一个有点人为的示例,但它允许考虑样本外预测的性能,并便于与 Stata 的文档进行比较)。
[10]:
# Dataset
raw = pd.read_stata(BytesIO(friedman2))
raw.index = raw.time
raw.index.freq = "QS-OCT"
data = raw.loc[:'1981']
# Variables
endog = data.loc['1959':, 'consump']
exog = sm.add_constant(data.loc['1959':, 'm2'])
nobs = endog.shape[0]
# Fit the model
mod = sm.tsa.statespace.SARIMAX(endog.loc[:'1978-01-01'], exog=exog.loc[:'1978-01-01'], order=(1,0,1))
fit_res = mod.fit(disp=False, maxiter=250)
print(fit_res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: consump No. Observations: 77
Model: SARIMAX(1, 0, 1) Log Likelihood -243.316
Date: Thu, 03 Oct 2024 AIC 496.633
Time: 16:06:22 BIC 508.352
Sample: 01-01-1959 HQIC 501.320
- 01-01-1978
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.6782 18.492 0.037 0.971 -35.565 36.922
m2 1.0379 0.021 50.329 0.000 0.997 1.078
ar.L1 0.8775 0.059 14.859 0.000 0.762 0.993
ma.L1 0.2771 0.108 2.572 0.010 0.066 0.488
sigma2 31.6979 4.683 6.769 0.000 22.520 40.876
===================================================================================
Ljung-Box (L1) (Q): 0.32 Jarque-Bera (JB): 6.05
Prob(Q): 0.57 Prob(JB): 0.05
Heteroskedasticity (H): 6.09 Skew: 0.57
Prob(H) (two-sided): 0.00 Kurtosis: 3.76
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
接下来,我们希望获得完整数据集的结果,但使用估计的参数(在数据的子集上)。
[11]:
mod = sm.tsa.statespace.SARIMAX(endog, exog=exog, order=(1,0,1))
res = mod.filter(fit_res.params)
predict 命令首先应用于此处以获取样本内预测。我们使用 full_results=True 参数来允许我们计算置信区间(predict 的默认输出只是预测值)。
如果没有其他参数,predict 将返回整个样本的单步预测样本内预测。
[12]:
# In-sample one-step-ahead predictions
predict = res.get_prediction()
predict_ci = predict.conf_int()
我们还可以获得动态预测。单步预测使用每一步的内生值的真实值来预测下一个样本内值。动态预测使用单步预测直到数据集中的某个点(由 dynamic 参数指定);之后,对于每个新的预测元素,使用先前的预测内生值来代替真实内生值。
dynamic 参数被指定为相对于 start 参数的偏移量。如果未指定 start,则假定为 0。
这里,我们执行从 1978 年第一季度开始的动态预测。
[13]:
# Dynamic predictions
predict_dy = res.get_prediction(dynamic='1978-01-01')
predict_dy_ci = predict_dy.conf_int()
我们可以绘制单步预测和动态预测(以及相应的置信区间)以查看其相对性能。请注意,直到动态预测开始的点(1978 年第一季度)之前,两者都是相同的。
[14]:
# Graph
fig, ax = plt.subplots(figsize=(9,4))
npre = 4
ax.set(title='Personal consumption', xlabel='Date', ylabel='Billions of dollars')
# Plot data points
data.loc['1977-07-01':, 'consump'].plot(ax=ax, style='o', label='Observed')
# Plot predictions
predict.predicted_mean.loc['1977-07-01':].plot(ax=ax, style='r--', label='One-step-ahead forecast')
ci = predict_ci.loc['1977-07-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='r', alpha=0.1)
predict_dy.predicted_mean.loc['1977-07-01':].plot(ax=ax, style='g', label='Dynamic forecast (1978)')
ci = predict_dy_ci.loc['1977-07-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='g', alpha=0.1)
legend = ax.legend(loc='lower right')
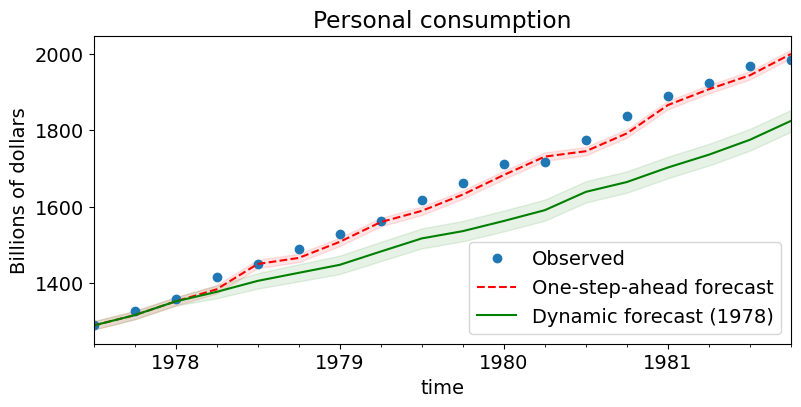
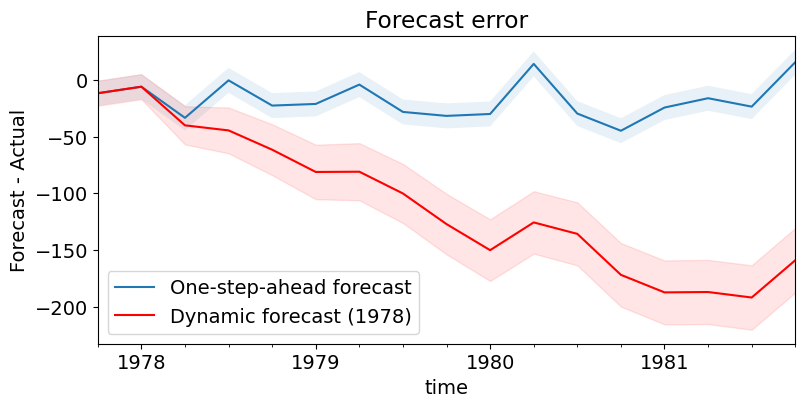
最后,绘制预测误差。很明显,正如预期的那样,单步预测要好得多。
[15]:
# Prediction error
# Graph
fig, ax = plt.subplots(figsize=(9,4))
npre = 4
ax.set(title='Forecast error', xlabel='Date', ylabel='Forecast - Actual')
# In-sample one-step-ahead predictions and 95% confidence intervals
predict_error = predict.predicted_mean - endog
predict_error.loc['1977-10-01':].plot(ax=ax, label='One-step-ahead forecast')
ci = predict_ci.loc['1977-10-01':].copy()
ci.iloc[:,0] -= endog.loc['1977-10-01':]
ci.iloc[:,1] -= endog.loc['1977-10-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], alpha=0.1)
# Dynamic predictions and 95% confidence intervals
predict_dy_error = predict_dy.predicted_mean - endog
predict_dy_error.loc['1977-10-01':].plot(ax=ax, style='r', label='Dynamic forecast (1978)')
ci = predict_dy_ci.loc['1977-10-01':].copy()
ci.iloc[:,0] -= endog.loc['1977-10-01':]
ci.iloc[:,1] -= endog.loc['1977-10-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='r', alpha=0.1)
legend = ax.legend(loc='lower left');
legend.get_frame().set_facecolor('w')